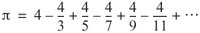Wrap-Up
Answers to Self Review Exercises
| 5.1 |
|
| 5.2 |
|
| 5.3 |
|
Introduction to Computers, the Internet and World Wide Web
- Introduction
- What Is a Computer?
- Computer Organization
- Early Operating Systems
- Personal, Distributed and Client/Server Computing
- The Internet and the World Wide Web
- Machine Languages, Assembly Languages and High-Level Languages
- History of C and C++
- C++ Standard Library
- History of Java
- FORTRAN, COBOL, Pascal and Ada
- Basic, Visual Basic, Visual C++, C# and .NET
- Key Software Trend: Object Technology
- Typical C++ Development Environment
- Notes About C++ and C++ How to Program, 5/e
- Test-Driving a C++ Application
- Software Engineering Case Study: Introduction to Object Technology and the UML (Required)
- Wrap-Up
- Web Resources
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Introduction to C++ Programming
- Introduction
- First Program in C++: Printing a Line of Text
- Modifying Our First C++ Program
- Another C++ Program: Adding Integers
- Memory Concepts
- Arithmetic
- Decision Making: Equality and Relational Operators
- (Optional) Software Engineering Case Study: Examining the ATM Requirements Document
- Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Introduction to Classes and Objects
- Introduction
- Classes, Objects, Member Functions and Data Members
- Overview of the Chapter Examples
- Defining a Class with a Member Function
- Defining a Member Function with a Parameter
- Data Members, set Functions and get Functions
- Initializing Objects with Constructors
- Placing a Class in a Separate File for Reusability
- Separating Interface from Implementation
- Validating Data with set Functions
- (Optional) Software Engineering Case Study: Identifying the Classes in the ATM Requirements Document
- Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Control Statements: Part 1
- Introduction
- Algorithms
- Pseudocode
- Control Structures
- if Selection Statement
- if...else Double-Selection Statement
- while Repetition Statement
- Formulating Algorithms: Counter-Controlled Repetition
- Formulating Algorithms: Sentinel-Controlled Repetition
- Formulating Algorithms: Nested Control Statements
- Assignment Operators
- Increment and Decrement Operators
- (Optional) Software Engineering Case Study: Identifying Class Attributes in the ATM System
- Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Control Statements: Part 2
- Introduction
- Essentials of Counter-Controlled Repetition
- for Repetition Statement
- Examples Using the for Statement
- do...while Repetition Statement
- switch Multiple-Selection Statement
- break and continue Statements
- Logical Operators
- Confusing Equality (==) and Assignment (=) Operators
- Structured Programming Summary
- (Optional) Software Engineering Case Study: Identifying Objects States and Activities in the ATM System
- Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Functions and an Introduction to Recursion
- Introduction
- Program Components in C++
- Math Library Functions
- Function Definitions with Multiple Parameters
- Function Prototypes and Argument Coercion
- C++ Standard Library Header Files
- Case Study: Random Number Generation
- Case Study: Game of Chance and Introducing enum
- Storage Classes
- Scope Rules
- Function Call Stack and Activation Records
- Functions with Empty Parameter Lists
- Inline Functions
- References and Reference Parameters
- Default Arguments
- Unary Scope Resolution Operator
- Function Overloading
- Function Templates
- Recursion
- Example Using Recursion: Fibonacci Series
- Recursion vs. Iteration
- (Optional) Software Engineering Case Study: Identifying Class Operations in the ATM System
- Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Arrays and Vectors
- Introduction
- Arrays
- Declaring Arrays
- Examples Using Arrays
- Passing Arrays to Functions
- Case Study: Class GradeBook Using an Array to Store Grades
- Searching Arrays with Linear Search
- Sorting Arrays with Insertion Sort
- Multidimensional Arrays
- Case Study: Class GradeBook Using a Two-Dimensional Array
- Introduction to C++ Standard Library Class Template vector
- (Optional) Software Engineering Case Study: Collaboration Among Objects in the ATM System
- Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
- Recursion Exercises
- vector Exercises
Pointers and Pointer-Based Strings
- Introduction
- Pointer Variable Declarations and Initialization
- Pointer Operators
- Passing Arguments to Functions by Reference with Pointers
- Using const with Pointers
- Selection Sort Using Pass-by-Reference
- sizeof Operators
- Pointer Expressions and Pointer Arithmetic
- Relationship Between Pointers and Arrays
- Arrays of Pointers
- Case Study: Card Shuffling and Dealing Simulation
- Function Pointers
- Introduction to Pointer-Based String Processing
- Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
- Special Section: Building Your Own Computer
- More Pointer Exercises
- String-Manipulation Exercises
- Special Section: Advanced String-Manipulation Exercises
- A Challenging String-Manipulation Project
Classes: A Deeper Look, Part 1
- Introduction
- Time Class Case Study
- Class Scope and Accessing Class Members
- Separating Interface from Implementation
- Access Functions and Utility Functions
- Time Class Case Study: Constructors with Default Arguments
- Destructors
- When Constructors and Destructors Are Called
- Time Class Case Study: A Subtle TrapReturning a Reference to a private Data Member
- Default Memberwise Assignment
- Software Reusability
- (Optional) Software Engineering Case Study: Starting to Program the Classes of the ATM System
- Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Classes: A Deeper Look, Part 2
- Introduction
- const (Constant) Objects and const Member Functions
- Composition: Objects as Members of Classes
- friend Functions and friend Classes
- Using the this Pointer
- Dynamic Memory Management with Operators new and delete
- static Class Members
- Data Abstraction and Information Hiding
- Container Classes and Iterators
- Proxy Classes
- Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Operator Overloading; String and Array Objects
- Introduction
- Fundamentals of Operator Overloading
- Restrictions on Operator Overloading
- Operator Functions as Class Members vs. Global Functions
- Overloading Stream Insertion and Stream Extraction Operators
- Overloading Unary Operators
- Overloading Binary Operators
- Case Study: Array Class
- Converting between Types
- Case Study: String Class
- Overloading ++ and --
- Case Study: A Date Class
- Standard Library Class string
- explicit Constructors
- Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Object-Oriented Programming: Inheritance
- Introduction
- Base Classes and Derived Classes
- protected Members
- Relationship between Base Classes and Derived Classes
- Constructors and Destructors in Derived Classes
- public, protected and private Inheritance
- Software Engineering with Inheritance
- Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Object-Oriented Programming: Polymorphism
- Introduction
- Polymorphism Examples
- Relationships Among Objects in an Inheritance Hierarchy
- Type Fields and switch Statements
- Abstract Classes and Pure virtual Functions
- Case Study: Payroll System Using Polymorphism
- (Optional) Polymorphism, Virtual Functions and Dynamic Binding Under the Hood
- Case Study: Payroll System Using Polymorphism and Run-Time Type Information with Downcasting, dynamic_cast, typeid and type_info
- Virtual Destructors
- (Optional) Software Engineering Case Study: Incorporating Inheritance into the ATM System
- Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Templates
- Introduction
- Function Templates
- Overloading Function Templates
- Class Templates
- Nontype Parameters and Default Types for Class Templates
- Notes on Templates and Inheritance
- Notes on Templates and Friends
- Notes on Templates and static Members
- Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Stream Input/Output
- Introduction
- Streams
- Stream Output
- Stream Input
- Unformatted I/O using read, write and gcount
- Introduction to Stream Manipulators
- Stream Format States and Stream Manipulators
- Stream Error States
- Tying an Output Stream to an Input Stream
- Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Exception Handling
- Introduction
- Exception-Handling Overview
- Example: Handling an Attempt to Divide by Zero
- When to Use Exception Handling
- Rethrowing an Exception
- Exception Specifications
- Processing Unexpected Exceptions
- Stack Unwinding
- Constructors, Destructors and Exception Handling
- Exceptions and Inheritance
- Processing new Failures
- Class auto_ptr and Dynamic Memory Allocation
- Standard Library Exception Hierarchy
- Other Error-Handling Techniques
- Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
File Processing
- Introduction
- The Data Hierarchy
- Files and Streams
- Creating a Sequential File
- Reading Data from a Sequential File
- Updating Sequential Files
- Random-Access Files
- Creating a Random-Access File
- Writing Data Randomly to a Random-Access File
- Reading from a Random-Access File Sequentially
- Case Study: A Transaction-Processing Program
- Input/Output of Objects
- Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Class string and String Stream Processing
- Introduction
- string Assignment and Concatenation
- Comparing strings
- Substrings
- Swapping strings
- string Characteristics
- Finding Strings and Characters in a string
- Replacing Characters in a string
- Inserting Characters into a string
- Conversion to C-Style Pointer-Based char * Strings
- Iterators
- String Stream Processing
- Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Web Programming
- Introduction
- HTTP Request Types
- Multitier Architecture
- Accessing Web Servers
- Apache HTTP Server
- Requesting XHTML Documents
- Introduction to CGI
- Simple HTTP Transactions
- Simple CGI Scripts
- Sending Input to a CGI Script
- Using XHTML Forms to Send Input
- Other Headers
- Case Study: An Interactive Web Page
- Cookies
- Server-Side Files
- Case Study: Shopping Cart
- Wrap-Up
- Internet and Web Resources
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Searching and Sorting
- Introduction
- Searching Algorithms
- Sorting Algorithms
- Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Data Structures
- Introduction
- Self-Referential Classes
- Dynamic Memory Allocation and Data Structures
- Linked Lists
- Stacks
- Queues
- Trees
- Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
- Special Section: Building Your Own Compiler
Bits, Characters, C-Strings and structs
- Introduction
- Structure Definitions
- Initializing Structures
- Using Structures with Functions
- typedef
- Example: High-Performance Card Shuffling and Dealing Simulation
- Bitwise Operators
- Bit Fields
- Character-Handling Library
- Pointer-Based String-Conversion Functions
- Search Functions of the Pointer-Based String-Handling Library
- Memory Functions of the Pointer-Based String-Handling Library
- Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Standard Template Library (STL)
- Introduction to the Standard Template Library (STL)
- Sequence Containers
- Associative Containers
- Container Adapters
- Algorithms
- Class bitset
- Function Objects
- Wrap-Up
- STL Internet and Web Resources
- Summary
- Terminology
- Self-Review Exercises
- Exercises
- Recommended Reading
Other Topics
- Introduction
- const_cast Operator
- namespaces
- Operator Keywords
- mutable Class Members
- Pointers to Class Members (.* and ->*)
- Multiple Inheritance
- Multiple Inheritance and virtual Base Classes
- Wrap-Up
- Closing Remarks
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Appendix A. Operator Precedence and Associativity Chart
Appendix B. ASCII Character Set
Appendix C. Fundamental Types
Appendix D. Number Systems
- D.1. Introduction
- D.2. Abbreviating Binary Numbers as Octal and Hexadecimal Numbers
- D.3. Converting Octal and Hexadecimal Numbers to Binary Numbers
- D.4. Converting from Binary, Octal or Hexadecimal to Decimal
- D.5. Converting from Decimal to Binary, Octal or Hexadecimal
- D.6. Negative Binary Numbers: Twos Complement Notation
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Appendix E. C Legacy Code Topics
- E.1. Introduction
- E.2. Redirecting Input/Output on UNIX/LINUX/Mac OS X and Windows Systems
- E.3. Variable-Length Argument Lists
- E.4. Using Command-Line Arguments
- E.5. Notes on Compiling Multiple-Source-File Programs
- E.6. Program Termination with exit and atexit
- E.7. The volatile Type Qualifier
- E.8. Suffixes for Integer and Floating-Point Constants
- E.9. Signal Handling
- E.10. Dynamic Memory Allocation with calloc and realloc
- E.11. The Unconditional Branch: goto
- E.12. Unions
- E.13. Linkage Specifications
- E.14. Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Appendix F. Preprocessor
- F.1. Introduction
- F.2. The #include Preprocessor Directive
- F.3. The #define Preprocessor Directive: Symbolic Constants
- F.4. The #define Preprocessor Directive: Macros
- F.5. Conditional Compilation
- F.6. The #error and #pragma Preprocessor Directives
- F.7. The # and ## Operators
- F.8. Predefined Symbolic Constants
- F.9. Assertions
- F.10. Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
- Exercises
Appendix G. ATM Case Study Code
- Appendix G. ATM Case Study Code
- G.1. ATM Case Study Implementation
- G.2. Class ATM
- G.3. Class Screen
- G.4. Class Keypad
- G.5. Class CashDispenser
- G.6. Class DepositSlot
- G.7. Class Account
- G.8. Class BankDatabase
- G.9. Class Transaction
- G.10. Class BalanceInquiry
- G.11. Class Withdrawal
- G.12. Class Deposit
- G.13. Test Program ATMCaseStudy.cpp
- G.14. Wrap-Up
Appendix H. UML 2: Additional Diagram Types
Appendix I. C++ Internet and Web Resources
- Appendix I. C++ Internet and Web Resources
- I.1. Resources
- I.2. Tutorials
- I.3. FAQs
- I.4. Visual C++
- I.5. Newsgroups
- I.6. Compilers and Development Tools
- I.7. Standard Template Library
Appendix J. Introduction to XHTML
- J.1. Introduction
- J.2. Editing XHTML
- J.3. First XHTML Example
- J.4. Headers
- J.5. Linking
- J.6. Images
- J.7. Special Characters and More Line Breaks
- J.8. Unordered Lists
- J.9. Nested and Ordered Lists
- J.10. Basic XHTML Tables
- J.11. Intermediate XHTML Tables and Formatting
- J.12. Basic XHTML Forms
- J.13. More Complex XHTML Forms
- J.14. Internet and World Wide Web Resources
- Summary
- Terminology
Appendix K. XHTML Special Characters
Appendix L. Using the Visual Studio .NET Debugger
- L.1. Introduction
- L.2. Breakpoints and the Continue Command
- L.3. The Locals and Watch Windows
- L.4. Controlling Execution Using the Step Into, Step Over, Step Out and Continue Commands
- L.5. The Autos Window
- L.6. Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
Appendix M. Using the GNU C++ Debugger
- M.1. Introduction
- M.2. Breakpoints and the run, stop, continue and print Commands
- M.3. The print and set Commands
- M.4. Controlling Execution Using the step, finish and next Commands
- M.5. The watch Command
- M.6. Wrap-Up
- Summary
- Terminology
- Self-Review Exercises
Bibliography
EAN: 2147483647
Pages: 627