Telegraphers Equations

Telegrapher s Equations

Figure 2.1 illustrates a variety of possible transmission structures. Popular configurations for long-distance digital communications include various types of coaxial cables and twisted-pair cables with and without shielding. Pcbs today most often use either microstrip or stripline traces. Transmission-line interconnections built on-chip typically use structures that resemble the microstrip, with either polysilicon or metal layers used for the conductors and a doped semiconductor substrate used as the underlying solid return path .

Figure 2.1. Useful transmission-line structures are available with a variety of cross sections.

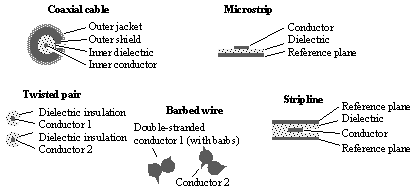
Surprisingly, you can model all these media with the same equations. Provided there exists a well-defined uniform path for the flow of both signal and return current, and further provided that the conductors are closely spaced in comparison to the wavelength of the signals conveyed, the telegrapher's equations accurately model the propagation of electrical currents and voltages along the structure. The telegrapher's equations were developed in the late 19th century to explain the behavior of high-speed signals on long telegraph lines and they still apply today . [4]

[4] In the 19th century "high-speed" Morse-code transmissions were accomplished in a batch processing mode at roughly 100 bits per second using automatic paper-tape transmission and recording devices.

A typical signal-transmission application comprises one or more long, uniform transmission lines hooked together with certain source and load impedances representing connectors and packages. To properly model such a system, you use the telegrapher's equations to create a two-port circuit model of each independent, long transmission structure, and then you combine the two-port models to determine the behavior of the entire system. The use of two-port analysis to predict overall system behavior is discussed extensively in Appendix C, " Two-Port Analysis." This chapter concentrates exclusively on the performance of one individual uniform transmission structure.

In general the telegrapher's equations may be successfully applied to any transmission media having the following characteristics:

• At least two conductors, insulated from each other,
• Having a uniform cross section along the entire length of the structure,
• With a cross-sectional geometry small compared to the wavelength of the signals conveyed, and
• A length long compared to the spacing between the conductors.

Any such structure, if properly terminated , may be used to convey high-speed data. One example of an unusual transmission structure is a railroad track. This works only in dry areas of the country where the tracks are not shorted together by ground moisture. The tracks have to be designed to maintain electrical continuity along their entire length.

A fascinating example of such a track is the Bay Area Rapid Transit (BART) system built in the early 1980's in the San Francisco region. This system uses light-gauge railroad tracks held off the ground on concrete pylons to avoid ground moisture. In the early versions of the system, digital control data was transmitted through the rails in a differential mode from the master control center to each train. The trains picked up and responded to the control signals through their metal wheels. The axles on each car were of course insulated from side to side to prevent shorting out the tracks. This system worked reasonably well until, after a few months of operation, the rust buildup on the tracks began to interfere with the rail-to-wheel electrical contact, producing intermittent behavior that foiled the system.

Another interesting transmission structure is a barbed-wire fence. The wires have to be supported on naturally insulating wooden fence poles, or metal poles with plastic insulators, to avoid shorting all the wires together. Such a structure might incorporate multiple conductors running perfectly parallel for miles. It might surprise you to know that practical communications systems working on barbed wire have been demonstrated at speeds as high as 1000 Mb/s (see "So Good It Works on Barbed Wire" in this chapter).

The reason the telegrapher's equations are so powerful and so widely used lies in the simple but flexible assumptions upon which they are built. In essence, the telegrapher's equations assume any transmission line may be modeled as a succession of small, independent elements, each with a transverse-electric-and-magnetic (TEM) wave configuration (see "TEM Wave Configuration" box). Each element represents a very short length of the line. Because each element is short, its performance is simple to describe. The telegrapher's equations then mathematically model the complete line as an infinite cascade of these short elements, taken in the limit as the length of each element approaches zero and the number of elements approaches infinity.

TEM Wave Configuration

The assumption of independence between the elements turns out to be quite important. If the signal leapfrogs, or jumps , directly from one element to another element without passing directly through the continuum of elements in their natural order, then the cascading equations used to build the telegrapher's model do not work. The telegrapher's equations only work for systems that don't have leapfrogging.

The assumption of independence between sections is equivalent to an assumption that the electromagnetic fields from one section do not interfere with subsequent sections. In the limit as the length of each segment is reduced, this principle of non-interference suggests that the lines of electric and magnetic flux from each segment must stick out sideways in a flat plane perpendicular to the direction of signal flow. They are not permitted to have any forward-and-back (longitudinal) components . This field configuration is called a transverse-electric-and-magnetic (TEM) pattern.

The telegrapher's equations in their basic form work only for transmission structures that support a simple TEM field pattern. Such structures include coaxial cables, pcb striplines, and all other configurations of two or more isolated conductors having a uniform cross section, a homogeneous dielectric, and a conductor spacing much smaller than the wavelength of the signals conveyed.

The telegrapher's equations model each short element of the transmission structure as a combination of two quantities (Figure 2.2):

Figure 2.2. The telegrapher's equations are based on this infinitely cascaded circuit model.

• An impedance z in series with the signal-and-return current, and
• An admittance y shunting the signal conductor to the return conductor.

Once you know z and y , the telegrapher's equations give you the input impedance and frequency response of the complete transmission structure. From those values you may compute the system response to any digital input.

For a typical transmission structure the series impedance z comprises the series resistance of the signal conductor, the series resistance of the return path, and the inductance represented by the combined loop of outgoing and returning current. The shunt admittance y comprises the parasitic capacitance between the signal and return conductors, and any DC leakage through the dielectric insulation separating the two. The series impedance and shunt admittance are defined in units of ohms-per-unit-length and Sieman-per-unit-length [5] respectively. Both quantities vary with frequency.

[5] One Sieman, the international standard unit of conductivity, is the inverse of an ohm, the unit of resistivity. An element of resistance r ohms has a conductivity of 1/ r Siemans.

2.1.1 So Good It Works on Barbed Wire

Article first published in EDN Magazine , July 5, 2001

In 1995, I had the privilege of serving as the chief technical editor of the Fast Ethernet specification. [6] In that capacity, I got to know many of the design teams working on chips to support the standard. The group from Broadcom was working particularly hard on an all-digital implementation of a subset of Fast Ethernet called 100BASE-T4 (different from the 100BASE-TX version that ultimately prevailed in the market).

Broadcom's T4 chip contained one of the first all-digital adaptive equalizers built for use on a fast serial link. Adaptive equalization was necessary in this case because the severely limited bandwidth of 100m of fairly low-grade category-3 data wiring filters out all the fast edges in a signal, turning a crisp transmitted signal into slush at the far end of the cable. A good adaptive equalizer reverses the filtering effect of the cable, restoring the received data to its normal appearance.

By 1995, the use of digital adaptive equalization at lower speeds was well-established, as in telephone and satellite modems. These products used programmable-DSP cores operating at speeds of approximately 100 Kbps. In contrast to the programmable approach, Broadcom used dedicated digital state machines to increase the speed of those same algorithms by a factor of 1000.

The value of the Broadcom T4 design was its ability to work at high speeds on horrible cables. In many cases, customers could use it on the cables they already had without upgrading to better cables. To demonstrate the power of what they felt was the world's best chip, the engineers at Broadcom decided to demonstrate the operation of their transceiver using the world's worst cable.

The "big four" transmission-line properties are impedance, delay, high-frequency loss, and crosstalk.

 

At Interop that year, Broadcom set up a 2x4-ft glass case containing eight parallel strands of barbed wire. The wires were configured as four differential pairs, each running straight from side to side, suspended in air. The wires were ugly and rusty, and had nasty little barbs all over them. A transmitter and a reel of category-3 data cabling were on one side of the case. The data cabling led to the glass case where it coupled onto the four barbed-wire pairs. The other side of the case coupled through more category-3 cabling to a receiver.

During the show, lo and behold, Broadcom's demonstration flawlessly conveyed 100 Mbps of data through the barbed wire. "Buy our parts " was the message the Broadcom marketing folks wanted to impress on their audience.

I'd like you to receive a different message: Only four properties really affect the performance of most digital transmission structures. The "big four" transmission-line properties are impedance, delay, high-frequency loss, and crosstalk.

 

Roger Billings extended the barbed-wire demo concept to even higher speeds, successfully conveying 1 Gb/s with his transceiver. Photo courtesy of Wideband Corporation, manufacturer of transceivers for Gigabit Ethernet and other standards.

 

1. Crosstalk in a barbed-wire configuration is controlled by enforcing a large spacing between the pairs, as compared with the much smaller spacing between the individual wires of each pair. The glass case in Broadcom's demonstration was easily large enough to accommodate such spacing, so crosstalk wasn't a problem.
2. What about the high-frequency loss? It wasn't a problem either. The T4 system divides its data among the four pairs so that each pair operates at only 25 Mbps. At that low frequency the skin-effect resistance of 4 ft of barbed wire is insignificant, and the overall high-frequency loss in the glass case at 25 Mbps was practically nil.
3. The signal delay is less on barbed wire than on an equivalent length of PVC-insulated category-3 wiring due to the use of an air dielectric between the barbed strands. This difference in delay was insignificant, however, because of the serial nature of the communications architecture.
4. Finally, if you consider the characteristic impedance, you find that this quantity is just a fixed number, such as 75 or 150 W . For most cables, it varies little with frequency between 1 and 100 MHz, but it varies significantly with the spacing between the wires. You can intentionally set the spacing to create almost any impedance you want. Inside the glass case, the spacing between barbed strands was set to create an impedance of 100 W ”the same impedance as in the category-3 UTP cabling on either side of the glass case. Thus, the case introduced no impedance discontinuity.

In summary, the barbed wire had zero impact on signal quality. The signals went through perfectly undistorted. The only thing the barbed wire did was impress the heck out of Broadcom's customers.

Next time you look at a transmission line, I hope you'll focus on the big four properties: characteristic impedance, high-frequency loss, delay, and crosstalk. These properties determine how well a transmission structure functions, regardless of the physical appearance or configuration of its conductors.

[6] Thanks to Paul Sherer at 3Com for sponsoring this work.

2.1.2 The No-Storage Principle and Its Implications for Returning Signal Current

The theory of lumped-element electrical circuits requires that no individual device store current, meaning that the currents into and out of every device must sum to zero. Expanding the no-storage principle to an entire network of devices, you may conclude that no network of lumped-element devices can store current. The current into the network equals the current out. Always.

In Figure 2.2 cut set A divides one stage from the next. In circuit theory, such a line completely partitioning one circuit network from another is called a cut set. Provided there are no other hidden paths for current between the two networks, the no-storage principle demands that the sum of currents crossing A must at all times precisely equal zero. In Figure 2.2 only two lines cross A , which makes the situation very simple ”the currents on the upper and lower wires crossing A must at all times be equal in magnitude but opposite in polarity.

Gustav Robert Kirchoff, the founder of modern circuit analysis, recognized the no-storage principle as central to his analysis of lumped-element circuits. By drawing tiny circles (cut sets) around each node in a network, he concluded that the sum of currents into and out of each circle must be zero. His conclusion is codified as Kirchoff's current law (KCL):

The sum of currents into any network node is zero .

You may draw a number of conclusions from the no-storage principle.

• For every signal current there must be an equal and opposite return current.
• Signal currents emanating from a digital chip generate equal but opposite return currents on the power and ground pins.
• The return current is equally as important as the signal current for noise, crosstalk, and EMC analysis.
• Current always makes a loop ”if it goes out, it must return.
• The sum of currents into any network node is zero (KCL).

Let's examine the assumptions behind these important conclusions to see when and under what conditions they apply. First I shall address a classic paradox involving the applicability of the no-storage principle: the vertical monopole 1/4-wave antenna. In that situation there exists a signal conductor, but apparently no return path, at least none in the sense of Kirchoff's lumped-element circuit analysis. Current flows on the signal conductor (the antenna wire) but nowhere else. How can this be?

Maxwell's equations provide a neat solution to this paradox. Maxwell determined that the concept of current comprises two distinct possibilities. The first possibility represents the physical movement of charged particles, as in ordinary current flowing on a wire. The second possibility is called displacement current. It represents the net effect of changes in the electric flux [7] entering or leaving a conducting body. The reason we must include displacement current in our electromagnetic field calculations is that the changing lines of electric flux, while they do not directly convey charged particles, push on the mobile charge carriers within other nearby conducting bodies, causing current to flow in them. In that sense, a changing electric flux acts just like ordinary current in that it pushes and pulls on the charges in other conductors, and so must be included in any accounting of total current flow. For near-field radiation problems, you may consider the displacement current flowing from one conducting body to another to be equivalent to the current that would flow through an appropriately sized parasitic capacitor connected directly between those two bodies.

[7] Electric flux is the integral of electric field intensity normal to a surface.

The reason Kirchoff gets away with ignoring displacement current is that he stipulates a priori that there shall be no stray electromagnetic fields flowing among the elements of any of his systems. This is what it means to be a lumped-element system . In that case the only possibility for the flow of current between elements is the direct transport of charged particles (on wires). Of course, Kirchoff understood that within the elements themselves (capacitors in particular), analysis of displacement current must be included, but in order to derive his simplified (and extremely useful) laws of circuit operation he set aside the possibility of external fields, thereby eliminating displacement current from his analysis.

Once you include the displacement current in the antenna analysis, you see that the current flowing into the antenna (the signal current) is matched by an equal and opposite current flowing out of the antenna (the displacement current). If you wish, you may track the electric flux through all of space to it various destinations, sum the totality of all currents induced in grounded objects that receive said electric flux, and account for the flow of physical current back through the Earth to the grounding rods of the transmitter through which the returning current flows back into the transmitting circuitry . Current (including displacement current) always makes a loop. If it's going out, it must be coming back. The only trick is, some of the returning current flows not through wires but through the action of parasitic capacitance.

Let us proceed one step further in the examination of the applicability of Kirchoff's laws by looking at the importance of the TEM assumption. The TEM assumption implies that the lines of electric and magnetic flux stick out sideways in a plane perpendicular to the direction of signal flow. This perpendicular field structure implies that the flux from one segment does not materially affect the next segment. In other words, TEM propagation precludes direct electromagnetic coupling (leapfrogging) between sections. Therefore, the telegrapher's equations need not contemplate any displacement current between sections, and Figure 2.2 need not show any connections between sections other than the upper (signal) and lower (return) wires.

Structures that do not adhere to the TEM mode of operation are not properly represented by Figure 2.2 and do not respond to the simple form of telegrapher's analysis presented here. Examples of non-TEM structures include microwave waveguide tubes with no central conductor, free-space radio propagation channels with multipath interference, and multimode fiber- optic cables.

As a final note, the conclusion about equal and opposite return currents is certainly affected by the degree to which Figure 2.2 properly represents the whole circuit. In systems where there exist a multitude of return-current pathways, different amounts of the returning signal current will flow along each path. To the extent that you provide one well-placed, intentional, continuous return-current path near the outgoing signal conductor, the loop inductance of the intentional return path in combination with your signal path will be much less than the effective loop inductance of more remote return pathways . Because high-frequency current flows most heavily on the path of least inductance, most of the return current will naturally flow on your intentional return pathway , so the magnitude of current in the intentional return path will be approximately the same as in the signal path. Systems in which there is no continuous return path or in which the return path is interrupted do not adhere to the TEM mode of operation. Such systems are not properly represented by Figure 2.2 and do not adhere to the telegrapher's analysis presented here.

POINTS TO REMEMBER

• Two long conductors insulated from each other with a uniform cross section make a good transmission line.
• The telegrapher's equations represent only the TEM mode of signal propagation.
• You can model almost any transmission line with the telegrapher's equations.