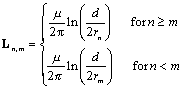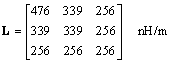Concentric-Ring Skin-Effect Model
The skin effect does not depend on any mysterious underlying forces. It may be completely predicted based on one simple, lumped-element equivalent model called the concentric-ring model.
Table 2.5. Assumptions Made by z BETTER
|
Conductor Geometry |
L i (0) |
|---|---|
|
Round wire of any radius not in close proximity to a return path ( k p = 1) |
|
|
Wire of any convex cross section with perimeter p and area a |
|
|
Rectangular wire of size w x t |
|
|
Square wire of size w x w |
|
|
Very thin rectangular wire, t << w |
|
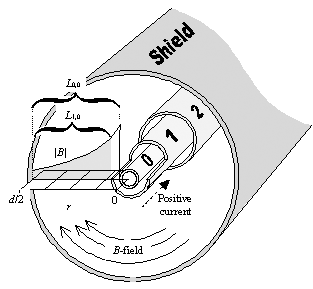
Imagine a round conductor divided lengthwise into concentric tubes, like the growth rings on a tree trunk. In this model the current proceeds absolutely parallel to the wire's central axis. Because current naturally passes straight down the trunk, parallel to the dividing boundaries between the rings, you may insulate the rings from each other without affecting the circuit. You now have a collection of n distinct, isolated conductors, shorted together only at each end of the trunk.
You may now separately consider the inductance of each ring. The inner rings, like long, skinny pipes, have more inductance than the outer rings, which are fatter. You know that at high frequencies, current follows the path of least inductance. Therefore, at high frequencies you should expect more current in the outer tree rings than in the inner. That is exactly what happens. At high frequencies the current crowds into the outermost rings. At low frequencies current partitions itself according to the resistance of each ring, while at high frequencies it partitions itself according of the inductance of each ring.
This simple concentric-ring idea motivates the idea of a redistribution of current at higher frequencies. What it doesn't do, however, is properly indicate the magnitude of the effect. The skin-effect mechanism is far more powerful than just the ratio of individual concentric-ring inductances. Mutual inductance between the rings actually bunches the current much more tightly onto the outer rings than you might at first imagine. The general setup for constructing a tree-ring model, including the mutual inductance, is discussed in the article "Modeling Skin Effect." The concentric-ring circuit model, if taken to an extreme (hundreds of thousands of rings), properly predicts both skin-effect resistance and skin-effect inductance, at low and high frequencies, for a circular conductor.
2.9.1 Modeling Skin Effect
2.9.2 Regarding Modeling Skin Effect
Email correspondence received July 17, 2001 SE HO YOU writesYou have shown an inductance matrix and indicated that since all the entries in the right column of the matrix are the same, ring number 2 concentrates all its flux into the space between ring number 2 and the shield. Would you please explain why flux concentrates around ring number 2? The behavior of the flux comes first, I think. Then, the inductance matrix should be just a mathematical expression of how nature works. Could you explain more physically? |
ReplyEddy currents flowing in the outer ring create a magnetic shield through which flux cannot penetrate . The shielding effect of the outermost ring therefore prevents flux from reaching the inner rings. Receiving no electromagnetic impulsion from changing flux, no current flows on the inner rings. At low frequencies the eddy currents in the outer ring are impeded by the resistance of the copper , so the shielding effect is imperfect. With an imperfect shield, some magnetic fields do reach the interior and some current does indeed flow on the inner rings. As you go to higher and higher frequencies, however, the shielding effect becomes more pronounced. The improved shielding effect successively robs the inner rings of more and more flux (and current). |
Fundamentals
- Impedance of Linear, Time-Invariant, Lumped-Element Circuits
- Power Ratios
- Rules of Scaling
- The Concept of Resonance
- Extra for Experts: Maximal Linear System Response to a Digital Input
Transmission Line Parameters
- Transmission Line Parameters
- Telegraphers Equations
- Derivation of Telegraphers Equations
- Ideal Transmission Line
- DC Resistance
- DC Conductance
- Skin Effect
- Skin-Effect Inductance
- Modeling Internal Impedance
- Concentric-Ring Skin-Effect Model
- Proximity Effect
- Surface Roughness
- Dielectric Effects
- Impedance in Series with the Return Path
- Slow-Wave Mode On-Chip
Performance Regions
- Performance Regions
- Signal Propagation Model
- Hierarchy of Regions
- Necessary Mathematics: Input Impedance and Transfer Function
- Lumped-Element Region
- RC Region
- LC Region (Constant-Loss Region)
- Skin-Effect Region
- Dielectric Loss Region
- Waveguide Dispersion Region
- Summary of Breakpoints Between Regions
- Equivalence Principle for Transmission Media
- Scaling Copper Transmission Media
- Scaling Multimode Fiber-Optic Cables
- Linear Equalization: Long Backplane Trace Example
- Adaptive Equalization: Accelerant Networks Transceiver
Frequency-Domain Modeling
- Frequency-Domain Modeling
- Going Nonlinear
- Approximations to the Fourier Transform
- Discrete Time Mapping
- Other Limitations of the FFT
- Normalizing the Output of an FFT Routine
- Useful Fourier Transform-Pairs
- Effect of Inadequate Sampling Rate
- Implementation of Frequency-Domain Simulation
- Embellishments
- Checking the Output of Your FFT Routine
Pcb (printed-circuit board) Traces
- Pcb (printed-circuit board) Traces
- Pcb Signal Propagation
- Limits to Attainable Distance
- Pcb Noise and Interference
- Pcb Connectors
- Modeling Vias
- The Future of On-Chip Interconnections
Differential Signaling
- Differential Signaling
- Single-Ended Circuits
- Two-Wire Circuits
- Differential Signaling
- Differential and Common-Mode Voltages and Currents
- Differential and Common-Mode Velocity
- Common-Mode Balance
- Common-Mode Range
- Differential to Common-Mode Conversion
- Differential Impedance
- Pcb Configurations
- Pcb Applications
- Intercabinet Applications
- LVDS Signaling
Generic Building-Cabling Standards
- Generic Building-Cabling Standards
- Generic Cabling Architecture
- SNR Budgeting
- Glossary of Cabling Terms
- Preferred Cable Combinations
- FAQ: Building-Cabling Practices
- Crossover Wiring
- Plenum-Rated Cables
- Laying Cables in an Uncooled Attic Space
- FAQ: Older Cable Types
100-Ohm Balanced Twisted-Pair Cabling
- 100-Ohm Balanced Twisted-Pair Cabling
- UTP Signal Propagation
- UTP Transmission Example: 10BASE-T
- UTP Noise and Interference
- UTP Connectors
- Issues with Screening
- Category-3 UTP at Elevated Temperature
150-Ohm STP-A Cabling
- 150-Ohm STP-A Cabling
- 150- W STP-A Signal Propagation
- 150- W STP-A Noise and Interference
- 150- W STP-A: Skew
- 150- W STP-A: Radiation and Safety
- 150- W STP-A: Comparison with UTP
- 150- W STP-A Connectors
Coaxial Cabling
- Coaxial Cabling
- Coaxial Signal Propagation
- Coaxial Cable Noise and Interference
- Coaxial Cable Connectors
Fiber-Optic Cabling
- Fiber-Optic Cabling
- Making Glass Fiber
- Finished Core Specifications
- Cabling the Fiber
- Wavelengths of Operation
- Multimode Glass Fiber-Optic Cabling
- Single-Mode Fiber-Optic Cabling
Clock Distribution
- Clock Distribution
- Extra Fries, Please
- Arithmetic of Clock Skew
- Clock Repeaters
- Stripline vs. Microstrip Delay
- Importance of Terminating Clock Lines
- Effect of Clock Receiver Thresholds
- Effect of Split Termination
- Intentional Delay Adjustments
- Driving Multiple Loads with Source Termination
- Daisy-Chain Clock Distribution
- The Jitters
- Power Supply Filtering for Clock Sources, Repeaters, and PLL Circuits
- Intentional Clock Modulation
- Reduced-Voltage Signaling
- Controlling Crosstalk on Clock Lines
- Reducing Emissions
Time-Domain Simulation Tools and Methods
- Ringing in a New Era
- Signal Integrity Simulation Process
- The Underlying Simulation Engine
- IBIS (I/O Buffer Information Specification)
- IBIS: History and Future Direction
- IBIS: Issues with Interpolation
- IBIS: Issues with SSO Noise
- Nature of EMC Work
- Power and Ground Resonance
Points to Remember
Appendix A. Building a Signal Integrity Department
Appendix B. Calculation of Loss Slope
Appendix C. Two-Port Analysis
- Appendix C. Two-Port Analysis
- Simple Cases Involving Transmission Lines
- Fully Configured Transmission Line
- Complicated Configurations
Appendix D. Accuracy of Pi Model
Appendix E. erf( )
Notes
EAN: N/A
Pages: 163

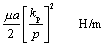
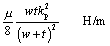

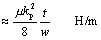

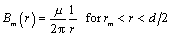 , where m is the magnetic permeability of the dielectric material (usually 4 p ·10 “7 H/m).
, where m is the magnetic permeability of the dielectric material (usually 4 p ·10 “7 H/m). m ) using Faraday's law as the integral of the magnetic-field strength, B m , taken over the range from conductor n (at radial position r n ) to the shield (at radial position d /2). Integrating 1/ r yields ln( r ) and the following matrix equations for mutual inductance (values for n < m are found using symmetry: L n,m = L m,n ):
m ) using Faraday's law as the integral of the magnetic-field strength, B m , taken over the range from conductor n (at radial position r n ) to the shield (at radial position d /2). Integrating 1/ r yields ln( r ) and the following matrix equations for mutual inductance (values for n < m are found using symmetry: L n,m = L m,n ):