Pcb (printed-circuit board) Traces

Pcb traces are used for extremely high-frequency connections within a single pcb and on backplanes connecting one or more pcbs. Figure 5.1 illustrates the microstrip, embedded microstrip, centered stripline, offset stripline , and coplanar waveguide structures as commonly employed in digital products.

Figure 5.1. Digital products employ a rich variety of pcb transmission-line structures.

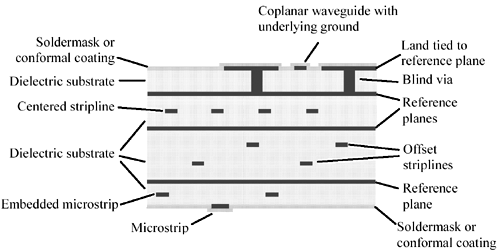
The microstrip trace has a solid reference plane on only one side. The stripline lies between two solid reference planes. A coplanar waveguide has grounded metal on either side of the trace, with or without a solid reference layer underneath.

Analysis of pcb performance generally relies on three assumptions about the pcb-trace geometry.

1. There exist well-defined uniform paths for the flow of both signal current and returning signal current.
2. The conductors are long compared to the spacing between the signal and return paths.
3. The conductors are shorter than the critical RC length l RC (see [3.56] in Section 3.5.1, "Boundary of RC Region").

Conditions 1 and 2 make possible the use of the telegrapher's equations. In high-speed digital designs these conditions generally imply the existence of a solid conducting reference plane underlying the signal conductors, although it is also possible to satisfy the conditions using a differential pair routed without a reference plane.

In the absence of a well-defined return-current path ”for example, in a two-layer pcb that may incorporate a grid of power and ground tracks instead of a solid reference plane ”one is relegated to analyzing each circuit as a large lumped-element structure (or a series of lumped-element structures) with randomized values of inductance and capacitance . In this situation the performance of individual traces at high speeds will be highly variable. Terminations may improve performance, but will not be a reliable means of controlling ringing, as the trace performance will change every time the trace is moved in successive layout passes .

Solid reference planes, if adjusted to the correct distance from each trace layer, endow all traces with a uniform impedance regardless of their routing, making possible the use of terminations as a reliable strategy for controlling ringing. Solid planes also have the side benefit of greatly reducing crosstalk between signals.

Condition 3 ensures that the total DC resistance of the trace remains a small fraction of the characteristic impedance. A trace under this condition never exhibits any noticeable RC behavior. It transitions directly from the lumped-element region (which applies at low frequencies) to the LC region (at higher frequencies) without passing through the RC region. Such traces have a fairly constant value of characteristic impedance at all frequencies above the lumped-element region, a property which simplifies the analysis. Figure 3.2 illustrates the critical RC length for a typical 50- W pcb trace of 150- m m (5.9-mil) width at about 2 meters (78 in.). [37] Analysis of longer traces must take into account the varying nature of characteristic impedance and attenuation in the RC region.

[37] The critical RC length is that length at which the outer boundary of the lumped-element region intersects the left edge of the LC region.

On-chip interconnections do not meet condition 3. They suffer from very high resistance in the metallization layer, due to the use of extremely thin metallic plating , and even higher resistance in the poly layers . As a result, most on-chip interconnections do in fact operate in the RC region.

When analyzing pcb traces shorter than 25 cm (10 in.) operating at edge rates no faster than 500 ps (1 GHz bandwidth), you can generally ignore trace losses. They just aren't significant enough to worry about. On longer traces or at higher speeds, the skin and dielectric losses can become quite significant.

POINT TO REMEMBER

• Analysis of pcb performance generally assumes:

  Well-defined uniform paths for both signal current and returning signal current.

  Conductors long compared to the spacing between the signal and return paths.

  Conductors shorter than the critical RC length l RC .

Pcb Signal Propagation