Embellishments

4.9.1 What If a Large Bulk-Transport Delay Causes the Waveform to Slide Off the End of the Time-Domain Window?

The waveform doesn't really fall off the end; it wraps around to the beginning (remember, FFT time is circular). The circular-shifting effect is particularly troublesome on lines operated above the LC-mode boundary, where it is possible to generate enormous bulk delays (many hundreds of bits) without much signal attenuation. In those cases it is possible for the signal to have wrapped around your FFT time window many times without your having noticed. The position of the observed waveform then becomes extremely sensitive to the exact bulk delay (very confusing).

To fix this problem, remove the bulk delay by applying (multiplying point-by-point) a comparable but opposite delay. The inverse-delay function is computed using the delay operator Dly with parameter t set to a negative value.

4.9.2 How Do I Transform an Arbitrary Data Sequence?

If the sampling rate is an exact multiple of the data bit time t b , then you have an easy job ahead of you.

Equation 4.19

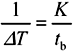
where t b is the data bit (or baud) time.

In this case the constant K is called the oversampling ratio .

First read the data pattern into a vector x u , where u 0,1..(length ( x ) “1).

Now define a new vector x' , which will hold a modified version of the input data sequence. The input sequence is expanded into the modified sequence by the method of repeating each value K times:

Equation 4.20

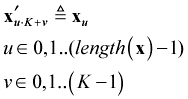
Use the normalized FFT to turn sequence x' , into a frequency-domain entity X and then apply edge filtering Gaus k and amplitude scaling D V in preparation for further processing.

Equation 4.21

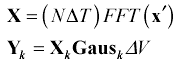
If the oversampling rate is not an exact multiple of the data rate, then you may construct the frequency-domain vector directly as a summation of variously delayed pulses . Take care that the full length of the data sequence fits within the FFT time window N D T .

Equation 4.22

 

where

parameter b for the pulse length PulB is set equal to the bit (or baud) interval t b . In this example the data train has been given Gaussian rising and falling edges and an amplitude D V .

The data sequence x u may be either binary (1 “0) or multivalued .

4.9.3 How Do I Shift the Time-Domain Waveforms?

Occasionally you will want to directly shift a time-domain waveform in order to line it up with some other signal for comparison. The most general-purpose method for accomplishing a shift is to use modulo arithmetic on the index variable of the time-domain vector x .

Equation 4.23

 

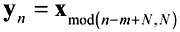
The new vector y is a shifted copy of the old vector x , delayed by m samples. The mod function avoids references to negative index values. It wraps the negative time points back around to index values near N , which is exactly how FFT time works. Values in FFT time that occur just before sample N will, if delayed by a few samples, wrap around to the front of the vector and show up just after time 0.

The time-domain circular shift is very handy for producing eye patterns, which are nothing more than multiple copies of x , delayed by various integral numbers of bit times and overlaid on top of each other.

4.9.4 What If I Want to Model a More Complicated System?

Two-port analysis handles some pretty complicated situations. See the comments at the end of Appendix C.

4.9.5 What About Differential Modeling?

You can model your differential-mode signal as a single-ended signal with characteristic impedance Z DIFF . A load of Z ohms connected across your differential line is modeled as a load of Z ohms to ground in the single-ended model. This approach models the differential signal, but not the common-mode signal, in your transmission environment.

Alternately, you could choose to model the odd-mode signal of your differential pair. The odd-mode signal equals the signal on one side of a purely differential transmission line, as opposed to the model mentioned previously, which models the difference between the two signals of a differential pair. The voltages in the odd-mode model are generally half those in the differential-mode model. An odd-mode model appears as a transmission line with an impedance equal to ½ Z DIFF = Z ODD . A load of Z ohms connected across your differential line is modeled as a load of Z /2 ohms to ground in the odd-mode model. This approach models the odd-mode signal, but not the even-mode signal, in your transmission environment.

The two-port analysis presented in Appendix C is not capable of modeling differential-to-common mode conversion problems or coupled transmission lines, but the frequency-domain approach can be made to work in that environment by using four-port matrices (two voltages and two currents on either side of each four-port matrix). A four-port transmission matrix, having four inputs and four outputs, is described by 16 internal cross-terms.

POINT TO REMEMBER

• Frequency-domain simulation handles some pretty complicated situations.