Slow-Wave Mode On-Chip

The term slow-wave mode applies exclusively to on-chip interconnections implemented in a metal-insulator-semiconductor (MIS) configuration. On such interconnections the substrate resistance adds substantially to the signal loss and can sometimes have the peculiar effect of greatly slowing signal propagation. The resulting slow-wave mode occurs when the substrate conductivity is adjusted so that electromagnetic fields only partially penetrate the substrate. The wave velocity then becomes a function of the substrate, not just the good dielectric insulation between the trace and the top layer of the substrate.

Figure 2.32 illustrates a classic on-chip MIS transmission line, comprising a metal trace, a 1- m m silicon dioxide insulating layer, and a 200- m m semiconducting substrate. The solid metal layer on the back of the substrate is called backside metallization . In this example I'll assume a worst-case value for the conductivity of the silicon substrate layer, about 50 S/m. At a frequency of 1 GHz, the intrinsic impedance h and skin depth d of the substrate are

Equation 2.106

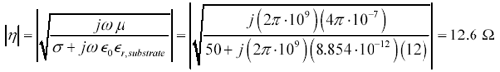
Equation 2.107

 

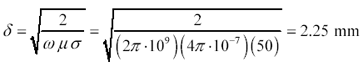
where	r,substrate is the complex permittivity of the substrate (F/m),
	m is the magnetic permeability (H/m), and
	s is the conductivity (S/m) of the substrate.
For nonmagnetic substrate materials, m = 4 p ·10 “7 H/m.

Figure 2.32. Metal-insulator-semiconductor (MIS) transmission lines suffer from the limited conductivity of the substrate.

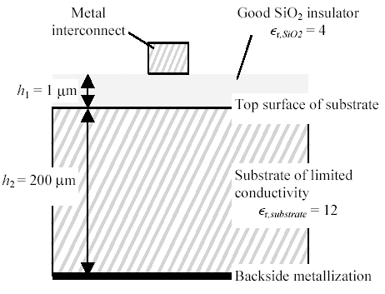
At 1 GHz the low intrinsic impedance of the substrate (12.6 ohms) prevents electric fields from penetrating . The transmission line therefore inherits a large amount of capacitance in accordance with the small distance h 1 between the trace and the top of the substrate.

Magnetic fields behave differently. At 1 GHz the penetration of magnetic fields (skin depth) greatly exceeds the thickness h 2 of the substrate, so the magnetic fields and their associated returning signal currents permeate the entire semiconducting substrate layer. The complete penetration of magnetic fields creates a large amount of inductance in accordance with the relatively large distance h 2 between the trace and the bottom of the substrate.

The difficulty with this circuit is that the electric and magnetic fields have become separated. In a perfect, homogeneous dielectric material, where the electric and magnetic fields both penetrate to the same depth, the velocity of propagation always equals .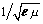

In this slow-wave example, the electric fields penetrate to a depth of h 1 , while the magnetic fields penetrate all the way down to h 2 , disconnecting the homogeneous assumption. The resulting combination of large capacitance and large inductance creates an absurdly slow velocity of signal propagation, much slower than would be indicated by the permittivity of either the insulator or the substrate acting alone.

In Figure 2.32 the velocity of propagation for a 1-GHz sine wave approaches 1/5 the speed of light in air. Furthermore, the complicated frequency dependencies associated with the slow-wave effect create significant phase distortion in the received waveform.

The slow-wave effect has been reported by numerous authors [16] , [17] , [18] . The consensus view about how to fix the problem is quite clear. You have three choices:

1. Raise the substrate conductivity by doping until it acts like a good, low-impedance return path . This approach shrinks the skin depth, forcing currents to flow mostly near the top surface of the semiconducting substrate. The line delay then depends only on the permittivity of the insulator (about 4.0 for silicon dioxide).
2. Decrease the substrate conductivity (by doping) until it acts like a good, high-impedance insulator. The electric and magnetic fields then completely penetrate the substrate layer together. The line delay in this case then depends mostly on the permittivity of the substrate (about 12.0 for lightly doped silicon). A high-speed chip requires backside metallization for this approach to work.
3. Add intentional metallic return paths near the signal traces.

In the world of pcb design, the dielectric materials have such a low conductivity that one almost always adopts the configuration of solution 2. This approach implies the existence of a solid-metal reference plane somewhere in the layer stack. The reference plane serves the same purpose in a pcb as the backside metallization in a chip ”it defines a good return-current path for all signals.

Occasionally, a board designer will implement solution 3. For example, in a 100BASE-TX interface, for the connection between the isolation transformer and the RJ-45 plug, you might use a co-planar differential pair with no underlying reference plane. The differential pair comprises a signal trace and an associated return-current conductor, so it meets the definition of solution 3.

In no case do pcb designers worry about the slow-wave mode or the implications of solution 1, because pcbs never use crummy, partly conducting substrates. That's one of the nice benefits of working at the printed-circuit design level.

The only way to separate the electric and magnetic fields on a pcb is to implement a nonuniform trace. For example, attaching hundreds of little cross-bars (like cilia) to a pcb trace adds a substantial amount of capacitance without changing the inductance, creating an absurdly low impedance and high delay.

POINT TO REMEMBER

• In an on-chip MIS configuration, if the electric fields penetrate to a depth of h 1 , while the magnetic fields penetrate to a futher depth h 2 , the resulting combination of large capacitance and large inductance creates an absurdly slow velocity of signal propagation.

 

For further study see: www.sigcon.com