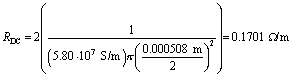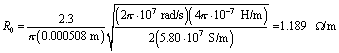UTP Signal Propagation

Electrical specifications for category 3, 5e, and 6 UTP, plus 150- W STP-A appear in TIA/EIA-568-B and are summarized in Table 8.1. Please note that these are cable specifications, not overall channel specifications. Channel specifications (which include connectors, jumper cables, work area cables, equipment cables, and other factors) are always worse (see note in Section 7.2, "SNR Budgeting").

Compared to category 3 cabling, categories 5e and 6 higher have progressively tighter twists and better plastic insulation with less dielectric loss at high frequencies. The resulting cables pick up less noise and have a superior frequency response (Table 8.1). Category 3 cabling is specified only up to 16 MHz, and therefore useful only up to about 25 Mbaud. Category 5e, 6, and 150- W STP-A carry the attenuation specifications up to higher frequencies.

Category 3 cabling, while no longer, widely available in the market, is included because many buildings still have this wire installed. Category 5e is a better choice for new buildings because it performs better and costs no more.

Compared to any of the UTP categories, 150- W STP-A specifies larger conductors (22 AWG versus 24 AWG) and higher characteristic impedance (150- W versus 100- W ). As a result, the 150- W STP-A bandwidth is much higher than either UTP category, and its performance is specified up to a higher frequency. Balancing these advantages are some severe practical disadvantages, discussed in Chapter 9. Although at the time of writing 150- W STP-A is recognized by TIA/EIA 568-B.2, it is not recommended for new cabling installations and may be dropped from future versions of that standard.

Table 8.1. TIA/EIA-568-B UTP and 150- W STP-A Electrical Specifications

Item	Cat-3	Cat-5e	Cat-6	150- W STP-A	Notes
H( w ) (dB)
0.064 MHz	0.9	”	”	”	Maximum allowable attenuation in dB per 100 m (328 ft) at 20 °C
0.256 MHz	1.3	”	”	”
0.512 MHz	1.8	”	”	”
0.772 MHz	2.2	1.8	1.8	”
1.0 MHz	2.6	2.0	2.0	”
4.0 MHz	5.6	4.1	3.8	2.2
8.0 MHz	8.5	5.8	5.3	3.1
10.0 MHz	9.7	6.5	6.0	3.6
16.0 MHz	13.1	8.2	7.6	4.4
20.0 MHz	”	9.3	8.5	4.9
25.0 MHz	”	10.4	9.5	6.2
31.25 MHz	”	11.7	10.7	6.9
62.5 MHz	”	17.0	15.4	9.8
100.0 MHz	”	22.0	19.8	12.3
200 MHz	”	”	29.0	”
250 MHz	”	”	32.8	”
300.0 MHz	”	”	”	21.4
Z C					Characteristic impedance (ohms) as measured on a 100 m length
Min	85	90	90	135
Max	115	110 [1]	110 [1]	165
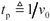
Max, at 10 MHz	5.45	5.45	5.45	5.45	Permitted group delay (ns/m) varies slightly as a function of frequency.

[1] NOTE (1) ”As implied by return loss specification.

POINT TO REMEMBER

• Compared to category 3 cabling, categories 5e and 6 higher have progressively tighter twists and better plastic insulation with less dielectric loss at high frequencies. The resulting cables pick up less noise and have a superior frequency response.

 

8.1.1 UTP Modeling

What follows is a discussion of how to compute the model parameters for UTP cables (see Section 3.1, "Signal Propagation Model"). Since 150- W STP-A is so similar to UTP, this section also develops the 150- W STP-A parameters at the same time.

For 24-gauge or similar cabling, parameter w should be set to 10 MHz ( w =2 p ·10 7 rad/s). Parameters Z and v appear directly in the specifications for UTP and 150- W STP-A cables. [65]

[65] TIA/EIA 568-B presents a formula for the worst-case cable delay at 10 MHz from which you may calculate v = 0.6116 c , which is rounded down to 0.6 c for all categories in Table 8.3.

R DC requires that you know the conductivity of annealed copper at 20 °C. The standards specify worst-case cable behavior at 20 °C. If your application operates at a significantly different temperature, increase the resistance by 0.39% per degree Centigrade. The formula for the DC resistance, per meter, of a UTP cable counts the resistance of both conductors (outbound and return). Hence, the factor of 2 appears on the left-hand side of this expression.

Equation 8.1

 

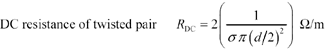
where	s is the conductivity of the conductors, S/m, and
	d is the conductor diameter, m.

Sometimes the total DC resistance of a cable (outbound plus return path included) is specified directly on the datasheet, in which case you may use that value instead of calculating it from the conductor diameter. Datasheet values must always be used for cables with complex conductor construction, such as copper-coated steel conductors, stranded conductors, or tin-plated conductors.

Example: Calculation of DC resistance for Category 3 UTP

For annealed copper as prepared for ordinary cables at 20 °C, s = 5.80 ·10 7 S/m.

For AWG 24 copper conductors, the diameter d = 0.508 mm.

 

The worst-case DC resistance for this grade of cabling is specified as 0.1876 W /m, suggesting that conductors with a diameter 5% smaller than nominal size AWG 24 are permitted under the standard.

To compute the skin-effect resistance R , you first need to compute the skin depth at frequency w . The following equation shows the calculation of skin depth as it ordinarily appears [69] .

Equation 8.2

 

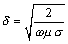
where	d is the skin depth, in meters ,
	w is the frequency at which the skin depth is specified, rad/sec,
	m is the magnetic permeability of the conductor in H/m, and
	s is the conductivity of the conductor, S/m.

Next use the skin depth to calculate the AC resistance of one of the signal conductors at frequency w . If the current distribution were uniform around the periphery of each conductor, the resistance would simply be 1/( p d d ( w ) s ). Unfortunately, life is not so simple.

The proximity effect distorts the pattern of current flow on the surface of the conductors, increasing the effective AC resistance by a fixed constant k p dependent on the conductor geometry (see Section 2.10.1, "Proximity Factor"). The proximity factors listed in Table 8.2 take into account the existence of two conductors (thus the values are each bigger than 2).

Equation 8.3

 

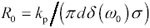
Expand d ( w ) according to [8.2].

Equation 8.4

 

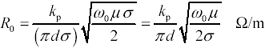
Table 8.2. Proximity Factors for Twisted-Pair Cabling

Cable type	Proximity factor k p
cat-3	2.3
cat-5e	2.3
cat-6	2.3
150- W STP-A	2.06

Example: Calculation of Nominal Skin-Effect Resistance for Category-3 UTP

Assume w = 2 p ·10 7 rad/sec (10 7 Hz).
	Copper being a nonmagnetic conductor, the magnetic permeability m = 4 p ·10 “7 H/m.
	For annealed copper as prepared for ordinary cables at 20 °C, s = 5.80 ·10 7 S/m.
	The proximity factor k p = 2.3 (Table 8.2).
	For AWG 24 copper conductors the nominal diameter d = 0.508 mm.

 

The best-fit value in Table 8.3 for the worst-case specifications indicates a skin-effect resistance of 1.452 W /m, suggesting that the worst-case specifications permit a combination of a diameter smaller than nominal size AWG 24, plating or other impurities in the surface layer of the copper, surface roughness effects, and measurement error combining to increase the nominal skin-effect resistance by 22%.

Note about dielectric loss : For PVC used below 40 °C, assume a nominal effective dielectric loss of q = 0.02 (Table 8.3 shows a best-fit, worst-case value of 0.01578 for category 3 UTP). Above 40 °C the PVC dielectric material typically used in category 3 cables exhibits a strong temperature dependence. Do not use PVC cable at temperatures greater than 40 °C, or 104 °F, a temperature easily attained in an enclosed attic. If you need to work at elevated temperatures , specify a less temperature-dependent cable, such as an FEP, PTFE, or PFA plenum-rated cable (see Section 8.6 "Category-3 UTP at Elevated Temperature.").

8.1.2 Adapting the Metallic-Transmission Model

As you might expect, the many possible combinations of surface plating, types of shielding, and dielectric make it difficult to accurately predict the performance of all twisted-pair cables from the basic information provided on a datasheet. Fortunately, the copper-based cable propagation model is highly adaptable. By only adjusting two parameters, you can easily produce a model that mimics the performance of just about any twisted-pair cable.

To adapt a model, start with [8.1] and [8.4] for DC resistance R DC and AC resistance R . That usually gets you pretty close to the worst-case frequency-domain specifications in the vicinity of w . Then tweak R , which scales the attenuation at all frequencies above the onset of the skin effect, and q , which increases the curvature of the attenuation graph at the very high end, until you get the best match to the worst-case specifications. That's how all the models in Table 8.3 were built. The "best match" criteria was a least-squares fit of the attenuation magnitude in dB. The models optimized for performance all the way down to DC match the worst-case specification to within 0.16 dB per 100 m at all specified frequencies.

The models optimized only over the frequency range above 1 MHz match the worst-case specification a little better, to within 0.03 dB at all specified frequencies. Modeling always works that way ”the more limited the domain of a model, the better it can match any arbitrary specification. The main difference between the copper-propagation model and the TIA/EIA model (other than that the copper-propagation model includes the correct phase information and is therefore useful for time-domain simulation) has to do with the treatment of the transition from the skin-effect mode to the LC (constant-loss) mode. TIA/EIA models accomplish this transition over the limited range of frequencies near 1 MHz by incorporating a frequency-response term proportional to 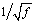. The TIA/EIA approach, while enjoying some theoretical basis as an approximation in the range near 1 MHz, is unrealizable in a physical cable and poorly mimics cable behavior below 1 MHz.

To force the metallic propagation model to conform to the unnatural behavior of the TIA/EIA model near 1 MHz, parameter R DC has been increased and R lowered . This adjustment better matches the worst-case TIA/EIA specifications at frequencies above 1 MHz by sacrificing the correct value of DC resistance.

Figure 8.2 compares the signal-propagation model of Chapter 3 to the TIA/EIA-568-B specifications.

Figure 8.2. Comparison of attenuation computed by metallic transmission model (solid lines) to EIA-568B specifications (points).

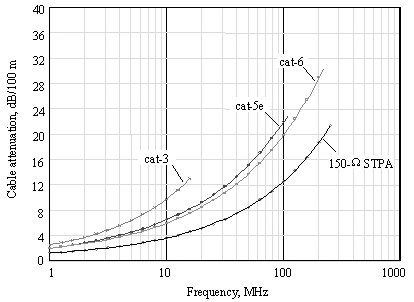
A perfect match is impossible to achieve. Standards often incorporate mysterious wobbles and bumps in their specifications, bumps that can't be matched with any rational modeling technique. No doubt these bumps are vestigial results of long-forgotten standards battles over compatibility with products that existed at the time. Also, remember that specifications represent a worst-case conglomeration of many effects. Each individual effect may cause the performance of a cable in the field to touch the specification limit at one particular frequency, but it may be impossible to construct a single cable that hugs the limit precisely at all frequencies. Lastly, keep in mind that cable installers rarely if ever calibrate their test equipment, and some of the tests aren't that accurate anyway. It is quite possible that you will see cables in the field certified for operation that don't quite meet the specifications.

Table 8.3. Worst-Case Transmission Line Parameters for TIA/EIA-568-B Cables

Cable type	Z W	v /c	R DC W /m	R W /m	q rad	w MHz	Useful range MHz	Max. error dB/100 m
Models optimized to include DC performance
cat-3	85	0.6	.1876	1.452	.01578	10	0 “16	.012
cat-5e	85	0.6	.1876	1.253	.001153	10	0 “100	.032
cat-6	90	0.6	.1876	1.257	.000447	10	0 “250	.161
150- W STP-A	135	0.6	.1142	1.134	.000658	10	0 “300	.164
Models optimized only from 1 MHz up
cat-6	90	0.6	.2902	1.208	.000965	10	1 “250	.028
150- W STP-A	135	0.6	.2855	1.061	.001136	10	1 “300	.013

Such is life. To respond to these problems, you should construct a rigorous cable model for system testing that either adds another 2 dB of fixed, flat loss to the standard or extends the simulated maximum cable length by another 10% to 20%. Transceiver designs that pass such testing will likely work well in the field.

Calculated worst-case (slowest) system step-response waveforms for 100 m of category 3, category 5e, category 6, and 150- W STP-A cabling appear in Figure 8.3. Longer or shorter cables scale the step response generally in proportion to the square of cable length. The step-response waveforms have been shifted horizontally to fit on the display.

Figure 8.3. Comparison of step-response waveforms for 100 m of cat-3, cat-5e, cat-6, and 150- W STP-A cabling (computed).

POINT TO REMEMBER

• The many possible combinations of surface plating, types of shielding, and dielectric make it difficult to accurately predict the performance of all twisted-pair cables from the basic information provided on a datasheet.
• The cable model you use for system simulation should either add another 2 dB of fixed, flat loss to the datasheet attenuation or extend the simulated maximum cable length by another 10% to 20%.