Customer Satisfaction Surveys

There are various ways to obtain customer feedback with regard to their satisfaction levels with the product(s) and the company. For example, telephone follow-up regarding a customer's satisfaction at a regular time after the purchase is a frequent practice by many companies. Other sources include customer complaint data, direct customer visits , customer advisory councils, user conferences, and the like. To obtain representative and comprehensive data, however, the time-honored approach is to conduct customer satisfaction surveys that are representative of the entire customer base.

14.1.1 Methods of Survey Data Collection

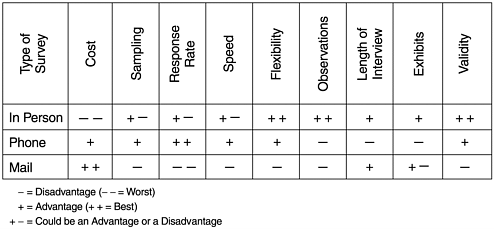
There are three common methods to gather survey data: face-to-face interviews, telephone interviews, and mailed questionnaires (self-administered). The personal interview method requires the interviewer to ask questions based on a prestructured questionnaire and to record the answers. The primary advantage of this method is the high degree of validity of the data. Specifically, the interviewer can note specific reactions and eliminate misunderstandings about the questions being asked. The major limitations are costs and factors concerning the interviewer. If not adequately trained, the interviewer may deviate from the required protocol, thus introducing biases into the data. If the interviewer cannot maintain neutrality, any statement, movement, or even facial expression by the interviewer could affect the response. Errors in recording the responses could also lead to erroneous results.

Telephone interviews are less expensive than face-to-face interviews. Different from personal interviews, telephone interviews can be monitored by the research team to ensure that the specified interview procedure is followed. The computer-aided approach can further reduce costs and increase efficiency. Telephone interviews should be kept short and impersonal to maintain the interest of the respondent. The limitations of this method are the lack of direct observation, the lack of using exhibits for explanation, and the limited group of potential respondents ”those who can be reached by telephone.

The mailed questionnaire method does not require interviewers and is therefore less expensive. However, this savings is usually at the expense of response rates. Low response rates can introduce biases to the data because if the respondents are different from the nonrespondents, the sample will not be representative of the population. Nonresponse can be a problem in any method of surveys, but the mailed questionnaire method usually has the lowest rate of response. For this method, extreme caution should be used when analyzing data and generalizing the results. Moreover, the questionnaire must be carefully constructed , validated , and pretested before final use. Questionnaire development requires professional knowledge and experience and should be dealt with accordingly . Texts on survey research methods provide useful guidelines and observations (e.g., Babbie, 1986).

Figure 14.1 shows the advantages and disadvantages of the three survey methods with regard to a number of attributes.

Figure 14.1. Advantages and Disadvantages of Three Survey Methods

14.1.2 Sampling Methods

When the customer base is large, it is too costly to survey all customers. Estimating the satisfaction level of the entire customer population through a representative sample is more efficient. To obtain representative samples, scientific probability sampling methods must be used. There are four basic types of probability sampling: simple random sampling, systematic sampling, stratified sampling, and cluster sampling.

If a sample of size n is drawn from a population in such a way that every possible sample of size n has the same chance of being selected, the sampling procedure is called simple random sampling. The sample thus obtained is called a simple random sample (Mendenhall et al., 1971). Simple random sampling is often mistaken as convenient sampling or accidental sampling for which the investigator just " randomly " and conveniently selects individuals he or she happens to come across. The latter is not a probability sample. To take a simple random sample, each individual in the population must be listed once and only once. Then some mechanical procedure (such as using a random number table or using a random number-generating computer program) is used to draw the sample. To avoid repeated drawing of one individual, it is usually more convenient to sample without replacement. Notice that on each successive draw the probability of an individual being selected increases slightly because there are fewer and fewer individuals left unselected from the population. If, on any given draw, the probabilities are equal of all remaining individuals being selected, then we have a simple random sample.

Systematic sampling is often used interchangeably with simple random sampling. Instead of using a table of random numbers , in systematic sampling one simply goes down a list taking every k th individual, starting with a randomly selected case among the first k individuals. ( k is the ratio between the size of the population and the size of the sample to be drawn. In other words, 1/ k is the sampling fraction.) For example, if we wanted to draw a sample of 500 customers from a population of 20,000, then k is 40. Starting with a random number between 1 and 40 (say, 23), then we would draw every fortieth on the list (63, 103, 143, . . . ).

Systematic sampling is simpler than random sampling if a list is extremely long or a large sample is to be drawn. However, there are two types of situations in which systematic sampling may introduce biases: (1) The entries on the list may have been ordered so that a trend occurs and (2) the list may possess some cyclical characteristic that coincides with the k value. For example, if the individuals have been listed according to rank and salary and the purpose of the survey is to estimate the average salary, then two systematic samples with different random starts will produce systematic differences in the sample means. As another example for bias (2), suppose in a housing development every twelfth dwelling unit is a corner unit. If the sampling fraction happens to be 1/12 ( k = 12), then one could obtain a sample either with all corner units or no corner units depending on the random start. This sample could be biased . Therefore, the ordering of a list should be examined before applying systematic sampling. Fortunately, neither type of problem occurs frequently in practice, and once discovered , it can be dealt with accordingly.

In a stratified sample, we first classify individuals into nonoverlapping groups, called strata, and then select simple random samples from each stratum. The strata are usually based on important variables pertaining to the parameter of interest. For example, customers with complex network systems may have a set of satisfaction criteria for software products that is very different from those who have standalone systems and simple applications. Therefore, a stratified sample should include customer type as a stratification variable.

Stratified sampling, when properly designed, is more efficient than simple random sampling and systematic sampling. Stratified samples can be designed to yield greater accuracy for the same cost, or for the same accuracy with less cost. By means of stratification we ensure that individuals in each stratum are well represented in the sample. In the simplest design, one can take a simple random sample within each stratum. The sampling fractions in each stratum may be equal (proportional stratified sampling) or different (disproportional stratified sampling). If the goal is to compare subpopulations of different sizes, it may be desirable to use disproportional stratified sampling. To yield the maximum efficiency for a sample design, the following guidelines for sample size allocation can be used: Make the sampling fraction for each stratum directly proportional to the standard deviation within the stratum and inversely proportional to the square root of the cost of each case in the stratum.

In stratified sampling we sample within each stratum. Sometimes it is advantageous to divide the population into a large number of groups, called clusters, and to sample among the clusters. A cluster sample is a simple random sample in which each sampling unit is a cluster of elements. Usually geographical units such as cities, districts, schools , or work plants are used as units for cluster sampling. Cluster sampling is generally less efficient than simple random sampling, but it is much more cost effective. The purpose is to select clusters as heterogeneous as possible but which are small enough to cut down on expenses such as travel costs involved in personal interviews. For example, if a company has many branch offices throughout the country and an in-depth face-to-face interview with a sample of its customers is desired, then a cluster sample using branch offices as clusters (of customers) may be the best sampling approach.

For any survey, the sampling design is of utmost importance in obtaining unbiased , representative data. If the design is poor, then despite its size, chances are the sample will yield biased results. There are plenty of real-life examples in the literature with regard to the successes and failures of sampling. The Literary Digest story is perhaps the most well known. The Literary Digest, a popular magazine in the 1930s, had established a reputation for successfully predicting winners of presidential elections on the basis of "straw polls ." In 1936 the Digest's history of successes came to a halt when it predicted a 3-to-2 victory for the Republican nominee, Governor Alf Landon, over the incumbent Franklin Roosevelt. As it turned out, Roosevelt won by a landslide, carrying 62% of the popular votes and 46 of the 48 states. The magazine suspended publication shortly after the election.

For the prediction, the Digest chose a sample of ten million persons originally selected from telephone listings and from the list of its subscribers. Despite the huge sample, the prediction was in error because the sample was not representative of the voting population. In the 1930s more Republicans than Democrats had telephones. Furthermore, the response rate was very low, about 20% to 25%. Therefore, the responses obtained from the poll and used for the prediction were not representative of those who voted (Bryson, 1976).

14.1.3 Sample Size

How large a sample is sufficient? The answer to this question depends on the confidence level we want and the margin of error we can tolerate . The higher the level of confidence we want from the sample estimate, and the smaller the error margin, the larger the sample we need, and vice versa. For each probability sampling method, specific formulas are available for calculating sample size, some of which (such as that for cluster sampling) are quite complicated. The following formula is for the sample size required to estimate a population proportion (e.g., percent satisfied) based on simple random sampling:

where

N	= population size
Z	= Z statistic from normal distribution: for  80%  confidence  level,   Z  =  1.28   for  85%  confidence  level,   Z  =  1.45   for  90%  confidence  level,   Z  =  1.65   for  95%  confidence  level,   Z  =  1.96
p	= estimated satisfaction level
B	= margin of error

A common misconception with regard to sample size is that the size of a sample must be a certain percentage of the population in order to be representative; in fact, the power of a sample depends on its absolute size. Regardless of the size of its population, the larger the sample the smaller its standard deviation will become and therefore the estimate will be more stable. When the sample size is up to a few thousands, it gives satisfactory results for many purposes, even if the population is extremely large. For example, sample sizes of national fertility surveys (representing all women of childbearing age for the entire nation) in many countries are in the range of 3,000 to 5,000.

Figure 14.2 illustrates the sample sizes for 10,000 customers for various levels of confidence with both 5% and 3% margins of error. Note that the required sample size decreases as the customer satisfaction level increases. This is because the larger the p value, the smaller its variance, p (1 “ p ) = pq . When an estimate for the satisfaction level is not available, using a value of 50% ( p = 0.5) will yield the largest sample size that is needed because pq is largest when p = q .

Figure 14.2. Examples of Sample Size (for 10,000 customers) in Relation to Confidence Level and Error Margin