Be Careful with Correlation

Correlation is probably the most widely used statistical method to assess relationships among observational data (versus experimental data). However, caution must be exercised when using correlation; otherwise , the true relationship under investigation may be disguised or misrepresented. There are several points about correlation that one has to know before using it. First, although there are special types of nonlinear correlation analysis available in statistical literature, most of the time when one mentions correlation, it means linear correlation. Indeed, the most well-known Pearson correlation coefficient assumes a linear relationship. Therefore, if a correlation coefficient between two variables is weak, it simply means there is no linear relationship between the two variables . It doesn't mean there is no relationship of any kind.

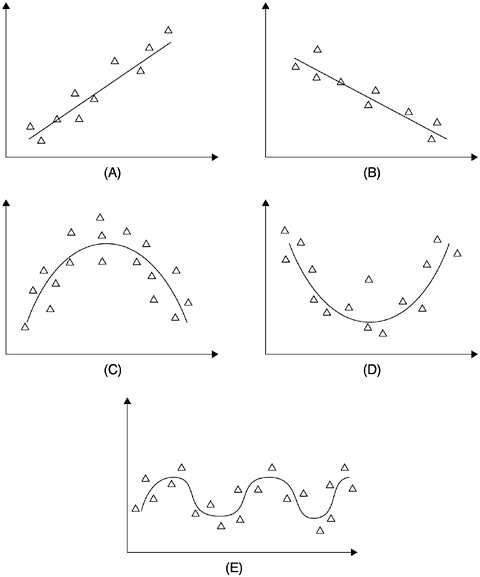
Let us look at the five types of relationship shown in Figure 3.6. Panel A represents a positive linear relationship and panel B a negative linear relationship. Panel C shows a curvilinear convex relationship, and panel D a concave relationship. In panel E, a cyclical relationship (such as the Fourier series representing frequency waves) is shown. Because correlation assumes linear relationships, when the correlation coefficients (Pearson) for the five relationships are calculated, the results accurately show that panels A and B have significant correlation. However, the correlation coefficients for the other three relationships will be very weak or will show no relationship at all. For this reason, it is highly recommended that when we use correlation we always look at the scattergrams. If the scattergram shows a particular type of nonlinear relationship, then we need to pursue analyses or coefficients other than linear correlation.

Figure 3.6. Five Types of Relationship Between Two Variables

Second, if the data contain noise (due to unreliability in measurement) or if the range of the data points is large, the correlation coefficient (Pearson) will probably show no relationship. In such a situation, we recommend using the rank-order correlation method, such as Spearman's rank-order correlation. The Pearson correlation (the correlation we usually refer to) requires interval scale data, whereas rank-order correlation requires only ordinal data. If there is too much noise in the interval data, the Pearson correlation coefficient thus calculated will be greatly attenuated. As discussed in the last section, if we know the reliability of the variables involved, we can adjust the resultant correlation. However, if we have no knowledge about the reliability of the variables, rank-order correlation will be more likely to detect the underlying relationship. Specifically, if the noises of the data did not affect the original ordering of the data points, then rank-order correlation will be more successful in representing the true relationship. Since both Pearson's correlation and Spearman's rank-order correlation are covered in basic statistics textbooks and are available in most statistical software packages, we need not get into the calculation details here.

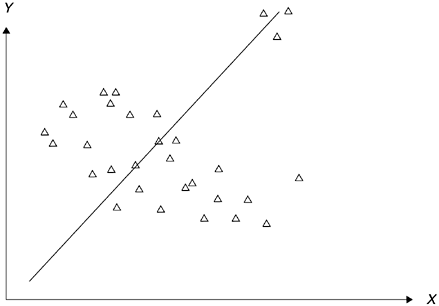
Third, the method of linear correlation (least-squares method) is very vulnerable to extreme values. If there are a few extreme outliers in the sample, the correlation coefficient may be seriously affected. For example, Figure 3.7 shows a moderately negative relationship between X and Y . However, because there are three extreme outliers at the northeast coordinates, the correlation coefficient will become positive. This outlier susceptibility reinforces the point that when correlation is used, one should also look at the scatter diagram of the data.

Figure 3.7. Effect of Outliers on Correlation

Finally, although a significant correlation demonstrates that an association exists between two variables, it does not automatically imply a cause-and-effect relationship. Although an element of causality, correlation alone is inadequate to show the existence of causality . In the next section, we discuss the criteria for establishing causality.