Ishikawas Seven Basic Tools

Ishikawa s Seven Basic Tools

Ishikawa's seven basic tools for quality control are checklist (or check sheet), Pareto diagram, histogram, scatter diagram, run chart, control chart, and cause-and-effect diagram. Figure 5.1 shows a simple representation of the tools.

Figure 5.1. Ishikawa's Seven Basic Tools for Quality Control

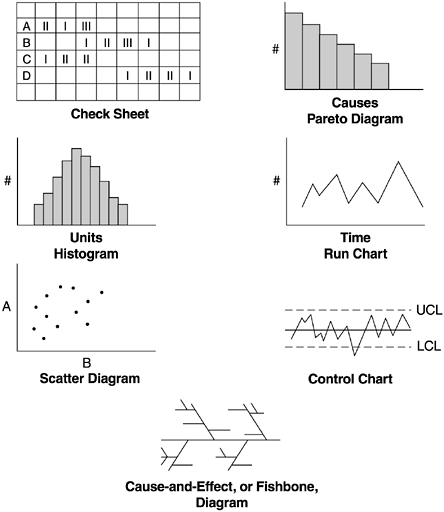
A check sheet is a paper form with printed items to be checked. Its main purposes are to facilitate gathering data and to arrange data while collecting it so the data can be easily used later. Another type of check sheet is the check-up confirmation sheet. It is concerned mainly with the quality characteristics of a process or a product. To distinguish this confirmation check sheet from the ordinary data-gathering check sheet, we use the term checklist. In most software development environments, the data-gathering aspect is automated electronically and goes far beyond the data-gathering checksheet approach, which has been used in manufacturing production. Our discussion on this tool, therefore, is confined to checklists.

A Pareto diagram is a frequency chart of bars in descending order; the frequency bars are usually associated with types of problems. It is named after a nineteenth-century Italian economist named Vilfredo Pareto (1848 “1923), who expounded his principle in terms of the distribution of wealth ”that a large share of the wealth is owned by a small percentage of the population. In 1950 Juran applied the principle to the identification of quality problems ”that most of the quality problems are due to a small percentage of the possible causes. In software development, the X -axis for a Pareto diagram is usually the defect cause and the Y -axis the defect count. By arranging the causes based on defect frequency, a Pareto diagram can identify the few causes that account for the majority of defects. It indicates which problems should be solved first in eliminating defects and improving the operation. Pareto analysis is commonly referred to as the 80 “20 principle (20% of the causes account for 80% of the defects), although the cause-defect relationship is not always in an 80 “20 distribution.

The histogram is a graphic representation of frequency counts of a sample or a population. The X -axis lists the unit intervals of a parameter (e.g., severity level of software defects) ranked in ascending order from left to right, and the Y -axis contains the frequency counts. In a histogram, the frequency bars are shown by the order of the X variable, whereas in a Pareto diagram the frequency bars are shown by order of the frequency counts. The purpose of the histogram is to show the distribution characteristics of a parameter such as overall shape, central tendency, dispersion, and skewness . It enhances understanding of the parameter of interest.

A scatter diagram vividly portrays the relationship of two interval variables . In a cause-effect relationship, the X -axis is for the independent variable and the Y -axis for the dependent variable. Each point in a scatter diagram represents an observation of both the dependent and independent variables. Scatter diagrams aid data-based decision making (e.g., if action is planned on the X variable and some effect is expected on the Y variable). One should always look for a scatter diagram when the correlation coefficient of two variables is presented. As discussed in Chapter 3, this is because the method for calculating the correlation coefficient is highly sensitive to outliers, and a scatter diagram can clearly expose any outliers in the relationship. Second, the most common correlation coefficient is Pearson's product moment correlation coefficient, which assumes a linear relationship. If the relationship is nonlinear, the Pearson correlation coefficient may show no relationship; therefore, it may convey incorrect or false information.

A run chart tracks the performance of the parameter of interest over time. The X- axis is time and the Y -axis is the value of the parameter. A run chart is best used for trend analysis, especially if historical data are available for comparisons with the current trend. Ishikawa (1989) includes various graphs such as the pie chart, bar graph, compound bar graph, and circle graph under the section that discusses run charts . An example of a run chart in software is the weekly number of open problems in the backlog; it shows the development team's workload of software fixes.

A control chart can be regarded as an advanced form of a run chart for situations where the process capability can be defined. It consists of a central line, a pair of control limits (and sometimes a pair of warning limits within the control limits), and values of the parameter of interest plotted on the chart, which represent the state of a process. The X -axis is real time. If all values of the parameter are within the control limits and show no particular tendency, the process is regarded as being in a controlled state. If they fall outside the control limits or indicate a trend, the process is considered out of control. Such cases call for causal analysis and corrective actions are to be taken.

The cause-and-effect diagram, also known as the fishbone diagram, was developed by Ishikawa and associates in the early 1950s in Japan. It was first used to explain factors that affect the production of steel . It is included in the Japanese Industrial Standards terminology for quality control (Kume, 1989). It shows the relationship between a quality characteristic and factors that affect that characteristic. Its layout resembles a fishbone, with the quality characteristic of interest labeled at the fish head, and factors affecting the characteristics placed where the bones are located. While the scatter diagram describes a specific bivariate relationship in detail, the cause-and-effect diagram identifies all causal factors of a quality characteristic in one chart.