Reliability and Predictive Validity
In Chapter 3 we examined issues associated with reliability and validity. In the context of modeling, reliability refers to the degree of change in the model output due to chance fluctuations in the input data. In specific statistical terms, reliability relates closely to the confidence interval of the estimate: The narrower the confidence interval, the more reliable the estimate, and vice versa. Confidence interval, in turn , is related to the sample size : Larger samples yield narrower confidence intervals. Therefore, for the Rayleigh model, which is implemented on a six-phase development process, the chance of having a satisfactory confidence interval is very slim. My recommendation is to use as many models as appropriate and rely on intermodel reliability to establish the reliability of the final estimates. For example, in addition to the Rayleigh model, one can attempt the exponential model or other reliability growth models (see Chapter 8). Although the confidence interval for each model estimate may not be satisfactory, if the estimates by different models are close to each other, confidence in the estimates is strengthened . In contrast, if the estimates from different models are not consistent, we will not have much confidence in our estimates even if the confidence interval for each single estimate is small. In such cases, more investigation is needed to understand and to reconcile the differences across models before a final estimate is decided.
Predictive validity refers simply to the accuracy of model estimates. The fore-most thing to achieve predictive validity is to make sure that the input data are accurate and reliable. As discussed in an earlier chapter, there is much room for improvement in data quality in the software industry in general, including defect tracking in software development. Within the development process, usually the tracking system and the data quality are better at the back end (testing) than at the front end (requirements analysis, design reviews, and code inspections). Without accurate data, it is impossible to obtain accurate estimates.
Second, and not less important, to establish predictive validity, model estimates and actual outcomes must be compared and empirical validity must be established. Such empirical validity is of utmost importance because the validity of software reliability models, according to the state of the art, is context specific. A model may work well in a certain development organization for a group of products using certain development processes, but not in dissimilar environments. No universally good software reliability model exists. By establishing empirical validity, we ensure that the model works in the intended context. For instance, when applying the Rayleigh to the AS/400 data, we verified the model based on many releases of the System/38 and System/36 data. We found that the Rayleigh model consistently underestimated the software field defect rate. To improve its predictive validity, we calibrated the model output with an adjustment factor, which is the mean difference between the Rayleigh estimates and the actual defect rates reported . The calibration is logical, given the similar structural parameters in the development process among the three computer systems, including organization, management, and work force.
Interestingly, Wiener-Ehrlich and associates also found that the Rayleigh model underestimated the manloading scores of a software project at the tail (Wiener-Ehrlich et al., 1984). It may be that the model is really too optimistic for software applications. A Weibull distribution with an m of less than 2 (for example, 1.8) might work better for software. This is a worthwhile research topic if reliable and complete data (including process as well as field defect data) for a large number of projects are available. It should be cautioned that when one models the data with the Weibull distribution to determine the value of the m parameter, one should be sure to use the complete data set. If incomplete data are used (e.g., in-process data for the current project), the m value thus obtained will be artificially high, which will lead to underestimates of the software defects. This is because m is the shape parameter of the Weibull distribution; it will fit the shape of the data points available during the estimation process. Therefore, for in-process data, a fixed m value should be used when modeling with the Weibull distribution. We have seen examples of misuse of the Weibull distribution with in-process data, resulting in invalid estimates of software defects.
To further test our observation that the Rayleigh model underestimates the tail end of the distribution of software data, we started to look for a meaningful set of data from another organization. We obtained the field defect arrival data for a systems software that was developed at IBM in Austin, Texas. The data set contains more than sixty monthly data points, representing the entire life cycle of field defects of the software. We fitted a number of software reliability models including the Rayleigh and the Weibull with several m values. As shown in Figure 7.6, we found that the Weibull model with m = 1.8 gave a better fit of the distribution than the Rayleigh model, although both pass the goodness-of-fit test.
Figure 7.6. Rayleigh Model Versus Weibull Distribution with m = 1.8
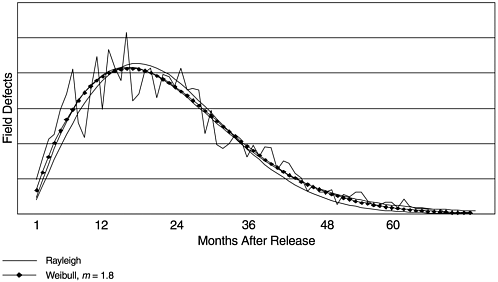
The three cases of Rayleigh underestimation discussed are from different software development organizations, and the time frame spans sixteen years from 1984 to 2000. Although more research is needed, based on the reasons discussed here, we recommend the use of Weibull with m = 2 in Rayleigh applications when estimation accuracy at the tail end is important.
What Is Software Quality?
Software Development Process Models
- Software Development Process Models
- The Waterfall Development Model
- The Prototyping Approach
- The Spiral Model
- The Iterative Development Process Model
- The Object-Oriented Development Process
- The Cleanroom Methodology
- The Defect Prevention Process
- Process Maturity Framework and Quality Standards
Fundamentals of Measurement Theory
- Fundamentals of Measurement Theory
- Definition, Operational Definition, and Measurement
- Level of Measurement
- Some Basic Measures
- Reliability and Validity
- Measurement Errors
- Be Careful with Correlation
- Criteria for Causality
Software Quality Metrics Overview
- Software Quality Metrics Overview
- Product Quality Metrics
- In-Process Quality Metrics
- Metrics for Software Maintenance
- Examples of Metrics Programs
- Collecting Software Engineering Data
Applying the Seven Basic Quality Tools in Software Development
- Applying the Seven Basic Quality Tools in Software Development
- Ishikawas Seven Basic Tools
- Checklist
- Pareto Diagram
- Histogram
- Run Charts
- Scatter Diagram
- Control Chart
- Cause-and-Effect Diagram
- Relations Diagram
Defect Removal Effectiveness
- Defect Removal Effectiveness
- Literature Review
- A Closer Look at Defect Removal Effectiveness
- Defect Removal Effectiveness and Quality Planning
- Cost Effectiveness of Phase Defect Removal
- Defect Removal Effectiveness and Process Maturity Level
The Rayleigh Model
- The Rayleigh Model
- Reliability Models
- The Rayleigh Model
- Basic Assumptions
- Implementation
- Reliability and Predictive Validity
Exponential Distribution and Reliability Growth Models
- Exponential Distribution and Reliability Growth Models
- The Exponential Model
- Reliability Growth Models
- Model Assumptions
- Criteria for Model Evaluation
- Modeling Process
- Test Compression Factor
- Estimating the Distribution of Total Defects over Time
Quality Management Models
- Quality Management Models
- The Rayleigh Model Framework
- Code Integration Pattern
- The PTR Submodel
- The PTR Arrival and Backlog Projection Model
- Reliability Growth Models
- Criteria for Model Evaluation
- In-Process Metrics and Reports
- Orthogonal Defect Classification
In-Process Metrics for Software Testing
- In-Process Metrics for Software Testing
- In-Process Metrics for Software Testing
- In-Process Metrics and Quality Management
- Possible Metrics for Acceptance Testing to Evaluate Vendor-Developed Software
- How Do You Know Your Product Is Good Enough to Ship?
Complexity Metrics and Models
- Complexity Metrics and Models
- Lines of Code
- Halsteads Software Science
- Cyclomatic Complexity
- Syntactic Constructs
- Structure Metrics
- An Example of Module Design Metrics in Practice
Metrics and Lessons Learned for Object-Oriented Projects
- Metrics and Lessons Learned for Object-Oriented Projects
- Object-Oriented Concepts and Constructs
- Design and Complexity Metrics
- Productivity Metrics
- Quality and Quality Management Metrics
- Lessons Learned from OO Projects
Availability Metrics
- Availability Metrics
- 1 Definition and Measurements of System Availability
- Reliability, Availability, and Defect Rate
- Collecting Customer Outage Data for Quality Improvement
Measuring and Analyzing Customer Satisfaction
- Measuring and Analyzing Customer Satisfaction
- Customer Satisfaction Surveys
- Analyzing Satisfaction Data
- Satisfaction with Company
- How Good Is Good Enough
Conducting In-Process Quality Assessments
- Conducting In-Process Quality Assessments
- The Preparation Phase
- The Evaluation Phase
- The Summarization Phase
- Recommendations and Risk Mitigation
Conducting Software Project Assessments
- Conducting Software Project Assessments
- Audit and Assessment
- Software Process Maturity Assessment and Software Project Assessment
- Software Process Assessment Cycle
- A Proposed Software Project Assessment Method
Dos and Donts of Software Process Improvement
- Dos and Donts of Software Process Improvement
- Measuring Process Maturity
- Measuring Process Capability
- Staged versus Continuous Debating Religion
- Measuring Levels Is Not Enough
- Establishing the Alignment Principle
- Take Time Getting Faster
- Keep It Simple or Face Decomplexification
- Measuring the Value of Process Improvement
- Measuring Process Adoption
- Measuring Process Compliance
- Celebrate the Journey, Not Just the Destination
Using Function Point Metrics to Measure Software Process Improvements
- Using Function Point Metrics to Measure Software Process Improvements
- Software Process Improvement Sequences
- Process Improvement Economics
- Measuring Process Improvements at Activity Levels
Concluding Remarks
- Concluding Remarks
- Data Quality Control
- Getting Started with a Software Metrics Program
- Software Quality Engineering Modeling
- Statistical Process Control in Software Development
A Project Assessment Questionnaire
EAN: 2147483647
Pages: 176
