Appendix C. Two-Port Analysis
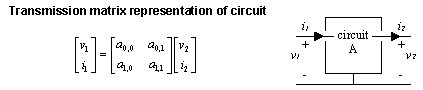
Figure C.1 depicts a generalized two-port circuit. The conventions for voltage and current preferred by this author are indicated. The figure assumes that both input and output ports share a common reference terminal, which is not strictly required for two-port analysis to work, but since the assumption conforms to the general situation in transmission-line analysis, the figure has been drawn that way.
Figure C.1. Any linear, time-invariant , two-port circuit can be represented by a four-element transmission matrix.
Two-port circuits are much studied in the field of electrical engineering, and you will find many references dealing with them. Beware that there is a great variation in the conventions for polarity of input and output currents and voltages, and in the definition of the elements that comprise the four-element matrix used to describe the frequency-response properties of the circuit.
Underlying all of two-port analysis is the assumption that the circuit under study is both linear and time-invariant. This assumption renders possible the use of a frequency-based description of the circuit. Nonlinear circuits do not succumb to linear two-port analysis.
In the figure, the four elements of the transmission matrix A prescribe the actions of the circuit. Each of the four elements of A is itself a function of frequency . The matrix specifies, for any particular frequency, the allowed relationships between the input and output currents and voltages at that frequency .
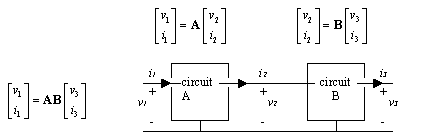
Of all the possible two-port definitions, your author has selected the transmission matrix version of two-port analysis for this book because it simplifies certain calculations often performed for cascaded systems . To explain, suppose two systems represented by two-port matrices A and B are cascaded as shown in Figure C.2. Matrix B converts the output parameters ( v 3 , i 3 ) into ( v 2 , i 2 ), and then matrix A converts ( v 2 , i 2 ) into ( v 1 , i 1 ). The overall two-port description of the system spanning from ( v 1 , i 1 ) to ( v 3 , i 3 ) is therefore given by the matrix product AB . This simple method of chaining together the two-port matrices accounts for the popularity of the transmission-matrix formulation.
Figure C.2. A cascade of circuits may be represented by multiplying their transmission matrices.
Let us derive from the four elements of a transmission matrix A the input impedance and gain of the circuit. The input impedance is calculated first assuming the output circuit ( v 2 , i 2 ) is open -circuited, meaning that i 2 = 0. Under that condition the matrix equations for ( v 1 , i 1 ) simplify to
Equation C.1
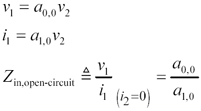
What if the output of the circuit is shorted to ground? In that case v 2 = 0, and the input impedance is again calculated using simplified matrix equations:
Equation C.2
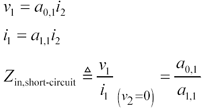
In the case of an open-circuited output, the voltage transfer function is computed from the first line of [C.1].
Equation C.3
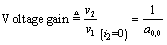
Fundamentals
- Impedance of Linear, Time-Invariant, Lumped-Element Circuits
- Power Ratios
- Rules of Scaling
- The Concept of Resonance
- Extra for Experts: Maximal Linear System Response to a Digital Input
Transmission Line Parameters
- Transmission Line Parameters
- Telegraphers Equations
- Derivation of Telegraphers Equations
- Ideal Transmission Line
- DC Resistance
- DC Conductance
- Skin Effect
- Skin-Effect Inductance
- Modeling Internal Impedance
- Concentric-Ring Skin-Effect Model
- Proximity Effect
- Surface Roughness
- Dielectric Effects
- Impedance in Series with the Return Path
- Slow-Wave Mode On-Chip
Performance Regions
- Performance Regions
- Signal Propagation Model
- Hierarchy of Regions
- Necessary Mathematics: Input Impedance and Transfer Function
- Lumped-Element Region
- RC Region
- LC Region (Constant-Loss Region)
- Skin-Effect Region
- Dielectric Loss Region
- Waveguide Dispersion Region
- Summary of Breakpoints Between Regions
- Equivalence Principle for Transmission Media
- Scaling Copper Transmission Media
- Scaling Multimode Fiber-Optic Cables
- Linear Equalization: Long Backplane Trace Example
- Adaptive Equalization: Accelerant Networks Transceiver
Frequency-Domain Modeling
- Frequency-Domain Modeling
- Going Nonlinear
- Approximations to the Fourier Transform
- Discrete Time Mapping
- Other Limitations of the FFT
- Normalizing the Output of an FFT Routine
- Useful Fourier Transform-Pairs
- Effect of Inadequate Sampling Rate
- Implementation of Frequency-Domain Simulation
- Embellishments
- Checking the Output of Your FFT Routine
Pcb (printed-circuit board) Traces
- Pcb (printed-circuit board) Traces
- Pcb Signal Propagation
- Limits to Attainable Distance
- Pcb Noise and Interference
- Pcb Connectors
- Modeling Vias
- The Future of On-Chip Interconnections
Differential Signaling
- Differential Signaling
- Single-Ended Circuits
- Two-Wire Circuits
- Differential Signaling
- Differential and Common-Mode Voltages and Currents
- Differential and Common-Mode Velocity
- Common-Mode Balance
- Common-Mode Range
- Differential to Common-Mode Conversion
- Differential Impedance
- Pcb Configurations
- Pcb Applications
- Intercabinet Applications
- LVDS Signaling
Generic Building-Cabling Standards
- Generic Building-Cabling Standards
- Generic Cabling Architecture
- SNR Budgeting
- Glossary of Cabling Terms
- Preferred Cable Combinations
- FAQ: Building-Cabling Practices
- Crossover Wiring
- Plenum-Rated Cables
- Laying Cables in an Uncooled Attic Space
- FAQ: Older Cable Types
100-Ohm Balanced Twisted-Pair Cabling
- 100-Ohm Balanced Twisted-Pair Cabling
- UTP Signal Propagation
- UTP Transmission Example: 10BASE-T
- UTP Noise and Interference
- UTP Connectors
- Issues with Screening
- Category-3 UTP at Elevated Temperature
150-Ohm STP-A Cabling
- 150-Ohm STP-A Cabling
- 150- W STP-A Signal Propagation
- 150- W STP-A Noise and Interference
- 150- W STP-A: Skew
- 150- W STP-A: Radiation and Safety
- 150- W STP-A: Comparison with UTP
- 150- W STP-A Connectors
Coaxial Cabling
- Coaxial Cabling
- Coaxial Signal Propagation
- Coaxial Cable Noise and Interference
- Coaxial Cable Connectors
Fiber-Optic Cabling
- Fiber-Optic Cabling
- Making Glass Fiber
- Finished Core Specifications
- Cabling the Fiber
- Wavelengths of Operation
- Multimode Glass Fiber-Optic Cabling
- Single-Mode Fiber-Optic Cabling
Clock Distribution
- Clock Distribution
- Extra Fries, Please
- Arithmetic of Clock Skew
- Clock Repeaters
- Stripline vs. Microstrip Delay
- Importance of Terminating Clock Lines
- Effect of Clock Receiver Thresholds
- Effect of Split Termination
- Intentional Delay Adjustments
- Driving Multiple Loads with Source Termination
- Daisy-Chain Clock Distribution
- The Jitters
- Power Supply Filtering for Clock Sources, Repeaters, and PLL Circuits
- Intentional Clock Modulation
- Reduced-Voltage Signaling
- Controlling Crosstalk on Clock Lines
- Reducing Emissions
Time-Domain Simulation Tools and Methods
- Ringing in a New Era
- Signal Integrity Simulation Process
- The Underlying Simulation Engine
- IBIS (I/O Buffer Information Specification)
- IBIS: History and Future Direction
- IBIS: Issues with Interpolation
- IBIS: Issues with SSO Noise
- Nature of EMC Work
- Power and Ground Resonance
Points to Remember
Appendix A. Building a Signal Integrity Department
Appendix B. Calculation of Loss Slope
Appendix C. Two-Port Analysis
- Appendix C. Two-Port Analysis
- Simple Cases Involving Transmission Lines
- Fully Configured Transmission Line
- Complicated Configurations
Appendix D. Accuracy of Pi Model
Appendix E. erf( )
Notes
EAN: N/A
Pages: 163
