Ideal Transmission Line
An ideal transmission line has these properties:
- No distortion
- No attenuation
Sufficient conditions for building an ideal transmission line are that you have two perfect conductors with zero resistance, uniform cross section, separation much smaller than the wavelength of the signals conveyed, and a perfect (lossless) dielectric. Voltages impressed upon one end of such an ideal transmission line will propagate forever, at constant velocity, without distortion or attenuation.
The propagation velocity , or transmission velocity , of a line is rated in units of m/s. The symbol for propagation velocity is v . This quantity indicates how far your signals will travel in every unit of time. For the case of perfect, zero-resistance conductors surrounded by a perfect vacuum , the propagation velocity equals c , the velocity of light in a vacuum, approximately 2.998 ·10 8 m/s. You may like to remember this constant in units convenient to your work, and with a precision commensurate with your needs, for instance 0.2998 m/ns (.3 m/ns), or 0.2998 mm/ps (.3 mm/ps), or perhaps 0.983 foot/ns (1 foot /ns).
The presence of any magnetic or dielectric materials near the conductors slows the propagation of electrical signals. If the conductors are embedded in a homogeneous dielectric material the velocity of propagation reduces to:
Equation 2.28
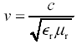
|
where |
[2.28] applies only to ideal, distortionless, lossless lines, |
|
v is the velocity of propagation (m/s), |
|
|
c is the velocity of light in vacuum (m/s), |
|
|
for lossless dielectric materials |
|
|
m r , a purely real quantity, is the relative magnetic permeability of the lossless material surrounding the conductors. |
Figure 2.6. Every TEM structure supports at least two modes.
Most digital applications involve the use of nonmagnetic dielectric insulating materials for which m r = 1; in that case expression [2.28] becomes
Equation 2.29
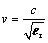
|
where |
[2.29] applies only to ideal, distortionless, lossless lines surrounded by a homogeneous nonmagnetic insulating material . |
If for some reason the insulating material surrounding the conductor is inhomogeneous (for example, a microstrip having dielectric material on one side and air on the other), then the dielectric material still has a slowing effect but not as great as if the material had completely surrounded the conductors.
Propagation delay per unit length is the inverse of velocity. This quantity indicates how much time elapses as your signal propagates some standard distance. If you are working in length-units of meters , the propagation delay of light in a vacuum is 3.336 ·10 “9 s/m.
Expressions [2.28] and [2.29] relate the velocity of propagation to the properties of the dielectric medium surrounding the conductors. The propagation velocity is also related to the quantities R , L , G , and C .
Using the mathematical language developed in the previous section, a lossless line requires R = G = 0. For this special case the formulas for impedance and propagation coefficient reduce to
Equation 2.30
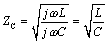
Equation 2.31
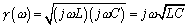
|
where |
the characteristic impedance Z C is a real quantity ( W ) independent of frequency, |
|
L (H/m) and C (F/m) are the per-unit-length values of inductance and capacitance respectively, and |
|
|
w is the frequency of operation (rad/s). |
The real and imaginary parts of g tell you the attenuation in units of nepers/m and phase delay in units of rad/m respectively. The transfer function for a unit length of ideal, distortionless, lossless transmission line is a simple linear-phase delay:
Equation 2.32
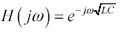
The real part of the propagation coefficient in [2.31] equals zero at all frequencies, indicating zero loss. The imaginary part of the propagation coefficient equals 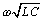 , a simple linear-phase delay. The prescribed delay per unit length equals
, a simple linear-phase delay. The prescribed delay per unit length equals  , and the velocity is the inverse of delay.
, and the velocity is the inverse of delay.
Equation 2.33
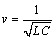
Take careful note of the units in these expressions. If L and C are rated in units of H/ u and F/ u respectively, where u is an arbitrary measure of length, then the propagation delay  appears in units of s/ u , the velocity in units of u /s, and the propagation coefficient in units of (complex) nepers per u .
appears in units of s/ u , the velocity in units of u /s, and the propagation coefficient in units of (complex) nepers per u .
Equating the two derivations of propagation velocity [2.28] and [2.33] reveals an important relationship between the quantities L , C , and the electrical properties of the insulating material.
Equation 2.34
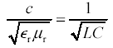
Equation [2.34] prescribes certain limits on your ability to independently modify L or C . No matter what modifications you make to one or the other of these variables , the product remains constant. [11] Equation [2.34] explains a peculiar property of stripline traces: A trace made wider to increase C enjoys a corresponding decrease in L , leaving the propagation velocity unchanged.
[11] Provided that the signal conductors remain uniform in cross section and embedded in a homogeneous dielectric.
Microstrip traces behave differently. Due to their inhomogeneous dielectric, modifications to trace width affect (slightly) the relative proportions of the electric field in the air versus in the dielectric material underneath the trace, and thus have a modest impact on trace velocity.
Datasheets for cables often rate transmission velocity in percent of c . A relative velocity of 66% would indicate a velocity v and delay 1/ v of
Equation 2.35

Example calculation of characteristic impedance and delay:
Measure the capacitance and inductance of RG-58/U coaxial cable, as shown in Figure 2.7, and then compute the delay. First cut off a 10-in. section of RG-58/U coaxial cable. Using a good-quality impedance meter, measure its capacitance. The correct value is 26 pF, which works out to 2.6 pF/in.
Figure 2.7. Measure capacitance with the far end of the line open -circuited and inductance with the far end of the line short-circuited.
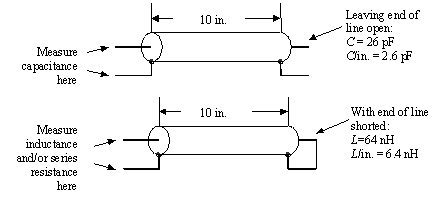
Next short out one end of the same 10-in. section and measure (from the other end) its inductance. [12] Here the correct value is 64 nH, which works out to 6.4 nH/in.
[12] One assumes the measurement of inductance is made at a frequency high enough that the skin effect has confined the flow of current to the surface of the conductors. Otherwise, a slightly higher value of inductance results, which slightly modifies the computed value of delay. If the conductors had zero resistivity, this change in inductance would never be observed , as the current would in no case penetrate the conductors.
Using a very sensitive four-terminal ohmmeter, you may notice that the center conductor of this cable also has a series resistance of 0.009 W , or 0.9 m W /in. Ideal transmission lines have zero resistance, but for our purposes right now the 10-in. segment of RG-58/U is close enough to ideal.
The per-unit-delay is  , precisely the value for RG-58/U listed in the Belden Wire and Cable Master Catalog 885.
, precisely the value for RG-58/U listed in the Belden Wire and Cable Master Catalog 885.
Our test sample of RG-58/U has a characteristic impedance of
Equation 2.36
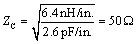
I am often asked why so much current is required to drive a long transmission line. To what good purpose is the current put? The function of the input current is simply this: to charge the parasitic capacitance of the line.
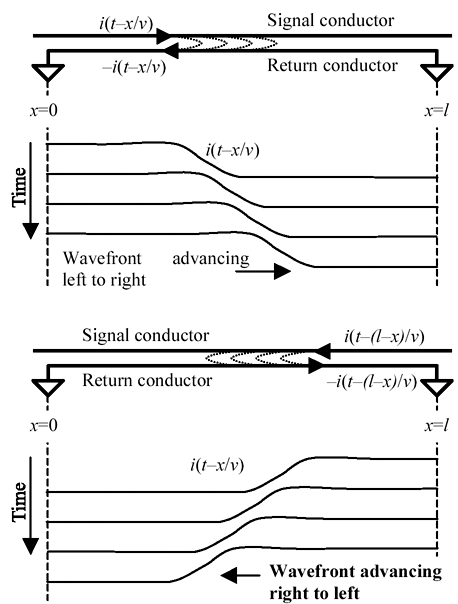
Figure 2.8 diagrams the patterns of voltage and current existing on a transmission line at two distinct snapshots separated in time by t d . Between snapshots, the rising wave front advances by physical distance vt d , where v is the propagation velocity of the transmission line.
Figure 2.8. Return current builds up simultaneously with the signal current as a rising edge propagates through a transmission structure.
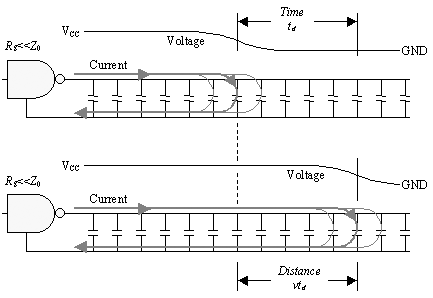
Each snapshot shows current flowing along the signal conductor from the driver to the leading edge of the wave front. Near the leading edge, current pours through the local parasitic capacitance of the line, changing its state, and then moves backwards along the return connection towards the driver. In each snapshot the current is being used to charge the parasitic capacitance of some chunk of line coinciding with the position of the rising edge at that moment.
Note that current flows only through the parasitic capacitance near the rising edge of the travelling waveform because that's where the voltage is changing . Current flows through capacitors only in response to changing voltages.
From the first moment when the driver begins to change state, a pattern immediately develops with current going into the line, charging up the first section of parasitic capacitance, and returning to the driver. As time progresses, the pattern stretches further down the line, but always with the coincidence of outgoing and return current. An understanding of this principle is fundamental to grasping the action of a transmission line. Current always makes a loop. It does not go down the signal conductor, reach the end, and then begin to make its way back. Rather, the outbound and returning paths build up together from the beginning. By the time the signal wave front reaches the end, the line has already established a complete pattern of outgoing and return current all along the structure.
Next let's look at how much current is required to support the movement of the advancing wave front. The figure shows that during interval t d the rising waveform must provide sufficient charge to all the capacitors along a span of length vt d . The change in voltage along this span goes from 0 to V CC . The total amount of capacitance contained within this span is Cvt d . The total amount of charge required is therefore q = V CC Cvt d . To provide this amount of charge within time t d requires a current of I = q / t d = V CC Cv .
Substituting 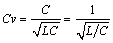 , the expression for I may be rewritten as
, the expression for I may be rewritten as  , which is precisely the amount of current you would expect during the first round trip, assuming a transmission-line characteristic impedance of
, which is precisely the amount of current you would expect during the first round trip, assuming a transmission-line characteristic impedance of 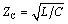 .
.
The above discussion shows that the characteristic impedance 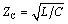 of an ideal transmission line is entirely accounted for by the current required to change the state of the line at the required propagation velocity v . The characteristic impedance of an ideal transmission line remains constant at all frequencies. It has no imaginary part and is not a function of frequency. It is a function only of the physical geometry of the transmission line and the dielectric constant of the insulation.
of an ideal transmission line is entirely accounted for by the current required to change the state of the line at the required propagation velocity v . The characteristic impedance of an ideal transmission line remains constant at all frequencies. It has no imaginary part and is not a function of frequency. It is a function only of the physical geometry of the transmission line and the dielectric constant of the insulation.
Practical values for characteristic impedance commonly range from a few ohms (between the inner and outer shields of triaxial cable) to 300 ohms (in a balanced configuration used for TV antenna connections).
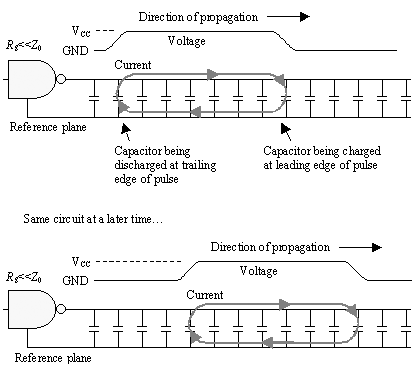
For your amusement (and because I get this question a lot), Figure 2.9 illustrates the patterns of current flow existing at various snapshots in time as a traveling wave pulse flows down a long transmission structure.
Figure 2.9. The current associated with a short-duration pulse creates a pattern reminiscent of a rolling tank tread.
POINTS TO REMEMBER
- A lossless transmission line requires R = G = 0.
- For the special case of a lossless line
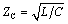 and
and 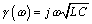 .
.
Fundamentals
- Impedance of Linear, Time-Invariant, Lumped-Element Circuits
- Power Ratios
- Rules of Scaling
- The Concept of Resonance
- Extra for Experts: Maximal Linear System Response to a Digital Input
Transmission Line Parameters
- Transmission Line Parameters
- Telegraphers Equations
- Derivation of Telegraphers Equations
- Ideal Transmission Line
- DC Resistance
- DC Conductance
- Skin Effect
- Skin-Effect Inductance
- Modeling Internal Impedance
- Concentric-Ring Skin-Effect Model
- Proximity Effect
- Surface Roughness
- Dielectric Effects
- Impedance in Series with the Return Path
- Slow-Wave Mode On-Chip
Performance Regions
- Performance Regions
- Signal Propagation Model
- Hierarchy of Regions
- Necessary Mathematics: Input Impedance and Transfer Function
- Lumped-Element Region
- RC Region
- LC Region (Constant-Loss Region)
- Skin-Effect Region
- Dielectric Loss Region
- Waveguide Dispersion Region
- Summary of Breakpoints Between Regions
- Equivalence Principle for Transmission Media
- Scaling Copper Transmission Media
- Scaling Multimode Fiber-Optic Cables
- Linear Equalization: Long Backplane Trace Example
- Adaptive Equalization: Accelerant Networks Transceiver
Frequency-Domain Modeling
- Frequency-Domain Modeling
- Going Nonlinear
- Approximations to the Fourier Transform
- Discrete Time Mapping
- Other Limitations of the FFT
- Normalizing the Output of an FFT Routine
- Useful Fourier Transform-Pairs
- Effect of Inadequate Sampling Rate
- Implementation of Frequency-Domain Simulation
- Embellishments
- Checking the Output of Your FFT Routine
Pcb (printed-circuit board) Traces
- Pcb (printed-circuit board) Traces
- Pcb Signal Propagation
- Limits to Attainable Distance
- Pcb Noise and Interference
- Pcb Connectors
- Modeling Vias
- The Future of On-Chip Interconnections
Differential Signaling
- Differential Signaling
- Single-Ended Circuits
- Two-Wire Circuits
- Differential Signaling
- Differential and Common-Mode Voltages and Currents
- Differential and Common-Mode Velocity
- Common-Mode Balance
- Common-Mode Range
- Differential to Common-Mode Conversion
- Differential Impedance
- Pcb Configurations
- Pcb Applications
- Intercabinet Applications
- LVDS Signaling
Generic Building-Cabling Standards
- Generic Building-Cabling Standards
- Generic Cabling Architecture
- SNR Budgeting
- Glossary of Cabling Terms
- Preferred Cable Combinations
- FAQ: Building-Cabling Practices
- Crossover Wiring
- Plenum-Rated Cables
- Laying Cables in an Uncooled Attic Space
- FAQ: Older Cable Types
100-Ohm Balanced Twisted-Pair Cabling
- 100-Ohm Balanced Twisted-Pair Cabling
- UTP Signal Propagation
- UTP Transmission Example: 10BASE-T
- UTP Noise and Interference
- UTP Connectors
- Issues with Screening
- Category-3 UTP at Elevated Temperature
150-Ohm STP-A Cabling
- 150-Ohm STP-A Cabling
- 150- W STP-A Signal Propagation
- 150- W STP-A Noise and Interference
- 150- W STP-A: Skew
- 150- W STP-A: Radiation and Safety
- 150- W STP-A: Comparison with UTP
- 150- W STP-A Connectors
Coaxial Cabling
- Coaxial Cabling
- Coaxial Signal Propagation
- Coaxial Cable Noise and Interference
- Coaxial Cable Connectors
Fiber-Optic Cabling
- Fiber-Optic Cabling
- Making Glass Fiber
- Finished Core Specifications
- Cabling the Fiber
- Wavelengths of Operation
- Multimode Glass Fiber-Optic Cabling
- Single-Mode Fiber-Optic Cabling
Clock Distribution
- Clock Distribution
- Extra Fries, Please
- Arithmetic of Clock Skew
- Clock Repeaters
- Stripline vs. Microstrip Delay
- Importance of Terminating Clock Lines
- Effect of Clock Receiver Thresholds
- Effect of Split Termination
- Intentional Delay Adjustments
- Driving Multiple Loads with Source Termination
- Daisy-Chain Clock Distribution
- The Jitters
- Power Supply Filtering for Clock Sources, Repeaters, and PLL Circuits
- Intentional Clock Modulation
- Reduced-Voltage Signaling
- Controlling Crosstalk on Clock Lines
- Reducing Emissions
Time-Domain Simulation Tools and Methods
- Ringing in a New Era
- Signal Integrity Simulation Process
- The Underlying Simulation Engine
- IBIS (I/O Buffer Information Specification)
- IBIS: History and Future Direction
- IBIS: Issues with Interpolation
- IBIS: Issues with SSO Noise
- Nature of EMC Work
- Power and Ground Resonance
Points to Remember
Appendix A. Building a Signal Integrity Department
Appendix B. Calculation of Loss Slope
Appendix C. Two-Port Analysis
- Appendix C. Two-Port Analysis
- Simple Cases Involving Transmission Lines
- Fully Configured Transmission Line
- Complicated Configurations
Appendix D. Accuracy of Pi Model
Appendix E. erf( )
Notes
EAN: N/A
Pages: 163
 r is a purely real quantity equal to the relative electric permittivity (a.k.a. dielectric constant) of the material surrounding the conductors, and
r is a purely real quantity equal to the relative electric permittivity (a.k.a. dielectric constant) of the material surrounding the conductors, and