Modeling Internal Impedance
The total per-unit-length series impedance z of any transmission line may be partitioned into external and internal series impedances: z = z e + z i .
The external series impedance z e represents mostly the inductance L e formed by magnetic flux occupying the spaces between the signal conductors (i.e., in dielectric insulating medium).
Equation 2.46

|
where |
L e is the external series inductance (H/m). |
The external series impedance z e also incorporates a small real part representing resistive losses encountered in the space surrounding the conductors (like radiation resistance). The resistive component of z e , I shall ignore under the assumption that conductors normally used for digital applications are designed not to significantly radiate.
Practical conductors posses two additional contributions to their series impedance: L i and R i . The internal inductance L i represents the magnetic flux that penetrates the walls of the conductor (see Figure 2.14). The term R i represents the resistance of the conductor. The internal impedance z i captures both resistive and inductive terms:
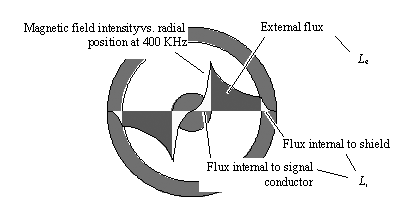
Figure 2.14. In this coaxial configuration a noticeable proportion of the low-frequency magnetic flux lies within the signal conductor and shield.
Equation 2.47

|
where |
R i is the internal series resistance ( W /m), and |
|
L i is the internal series inductance (H/m). |
As you move to higher and higher frequencies the magnetic fields (and associated currents) penetrate the walls of the conductors less and less significantly, thus shrinking the internal inductance and raising the internal resistance. Figure 2.15 captures the changes to internal inductance and resistance that happen within an RG-58/U coaxial cable.
Figure 2.15. Below the onset of the skin effect both L i and R i hold constant.

Below w d (the skin-effect onset frequency), both resistance and inductance hold constant. The internal resistance is determined by the conductivity and cross-sectional area of the conductors, while the internal inductance depends on the conductor geometry. For round conductors, the low frequency value of internal inductance is m /8 p . For other conductor shapes (like square or rectangular conductors), the internal inductance is undoubtedly less; however, the exact value of internal inductance for an arbitrary shape is not easily calculated.
Above w d , the internal resistance R i grows in proportion to the square root of frequency, while the internal inductance L i shrinks at the same rate. This result holds for all good conductors , meaning materials for which ( s >> w e ), a property shared by most metals up to extremely high (i.e., optical) frequencies. In all but the lowest -impedance transmission configurations L e exceeds L i by a substantial factor even at DC, with the difference becoming even more pronounced about w d . Not far above w d , the internal inductance shrinks to insignificance.
Table 2.4 summarizes the asymptotic values of R i and L i for a round conductor , assuming it is located sufficiently far from its return path so k p = 1.
A complete derivation of the distribution of current within a round conductor appears in [19] and [15] . Unfortunately, the derivation may be obtained only at the high mental cost of invoking Bessel functions. These derivations apply to the case of one round conductor exposed to a uniform electric field oriented along the axis of the conductor. The conductor must be made of a "good conductor" material for which s greatly exceeds w e at all frequencies of interest (a good assumption for almost all metals). Under these assumptions, the value of L i due to redistribution of current within the center conductor equals precisely m /8 p . The complete form of the internal impedance z i for a round conductor is
Equation 2.48
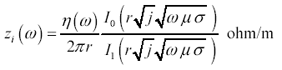
|
where |
h is the intrinsic impedance of a good conducting material, |
|
I and I 1 are modified Bessel functions of order zero and one respectively, |
|
|
w is the frequency of operation (rad/s), |
|
|
m is the magnetic permeability of the conducting material (H/m), |
|
|
s is the conductivity of the conducting material (S/m), and |
|
|
r is the radius of the wire (m). |
|
|
The value of m for nonmagnetic materials is 4 p ·10 “7 (H/m). |
|
|
For annealed copper at room temperature, s = 5.800 ·10 7 (S/m) . |
|
In general, the intrinsic impedance of a material is given by 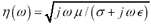 . In a good conductor, however, the term s greatly exceeds j w
. In a good conductor, however, the term s greatly exceeds j w  at all frequencies, so the intrinsic impedance reduces to
at all frequencies, so the intrinsic impedance reduces to 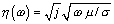 . The intrinsic impedance of a good conductor therefore takes on the phase angle of
. The intrinsic impedance of a good conductor therefore takes on the phase angle of 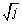 , which precisely equals p /4.
, which precisely equals p /4.
When evaluating [2.48], you need to know that many software implementations of the modified Bessel functions I and I 1 exist for real-valued arguments, but few accept complex arguments. That problem may be solved by resorting to two specially tabulated Bessel functions, ber n ( v ) and bei n ( v ), defined in the following way:
Table 2.4. Round-Wire Values for R i and L i , Assuming k p = 1 and k a = 1
|
w << w d |
w >> w d |
|
|---|---|---|
|
Internal resistance R i ( W /m) |
|
|
|
Internal inductance L i (H/m) |
|
|
|
Internal impedance z i = R i + j w L i ( W /m) |
|
|
|
NOTE ”Where a is the cross-sectional area (m 2 ), p is the perimeter of a cross-section of the signal conductor (m), s is the conductivity (S/m), and m is the permeability (H/m) of the conductor. The operating frequency is w (rad/s). The conductor is assumed smooth and well separated from a large, low-resistance return path. |
||
Equation 2.49
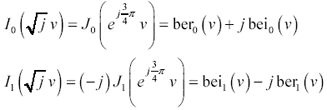
The functions ber n ( v ) and bei n ( v ) are available in MathCad, where they go by the name of the Bessel Kelvin functions. These same functions are tabulated elsewhere [6] , [7] .
Figure 2.16 plots the internal impedance predicted by [2.48]. Please keep in mind that equation [2.48] works only for round wires. Figure 2.16 depicts the real and imaginary parts of the complex internal impedance, R i and j w L i , slightly different from the parameters R i and L i (without the j w ) shown in Figure 2.15. One fascinating aspect of this figure is how, at high frequencies, the real and imaginary parts of complex internal impedance converge to a common value. This convergence reveals a deep connection between the real and imaginary parts of any network function. Any causal , minimum-phase impedance function growing at a flat rate of +10 dB/ decade must have a phase angle of exactly p /4. The phase angle of p /4 bestows upon the function equal real and imaginary parts.
Figure 2.16. Equation [2.48] for round wires predicts both real and imaginary parts of the internal impedance.
2.8.1 Practical Modeling of Internal Impedance
Although the closed-form model [2.48] is mathematically quite beautiful, it isn't widely used for two reasons:
- It is too computationally intensive .
- It works only for round wires, not rectangular.
For most signal-integrity simulations, an approximation will suffice. I'll present two possibilities here. The basic approximation produces the correct asymptotic behavior at DC and at high frequencies, but lacks accuracy in the transition region. The better approximation provides improved accuracy in the transition region. Both approximations use the same parameters:
|
w |
Frequency of operation (rad/s). |
|
R DC |
The total DC series resistance per meter of the transmission line ( W /m), |
|
w |
A particular frequency (rad/s), chosen well above the onset of the skin effect but below the onset of surface roughness and non-TEM modes, and |
|
R |
The real part of the skin-effect impedance at the particular frequency w . ( W /m). R should be set to take into account the proximity effect, if present, although in the following discussion for round-wire problems not in proximity to other conductors, you may assume k p |
Both approximations use the same expression for the high-frequency (AC) series impedance of the wire. Note that this expression comprises equal real and imaginary parts, meaning a phase angle of 45 degrees, which is correct for a causal, minimum-phase network function with a slope of +10 dB/decade.
Equation 2.50

In both cases the real part of z i will be identified as the internal resistance, while the imaginary part of z i will be interpreted as the internal inductance: 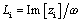 .
.
Here are the two approximations for z i .
Simple approximation:
Equation 2.51
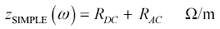
Better approximation:
Equation 2.52
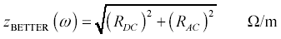
Figure 2.17 compares both approximations to the Bessel-function solution for a round wire. The asymptotic behavior of both functions is good. Both functions produce the correct impedance at very high frequencies, with the correct upward tilt of +10 dB/decade and a phase angle of +45 degrees. They also both produce the correct DC resistance at low frequencies. The difference between them lies in their behavior near the skin-effect onset frequency and in the predicted value of internal inductance.
Figure 2.17. Two decades to either side of the skin-effect onset frequency, the real part of z SIMPLE still errs by 10%.
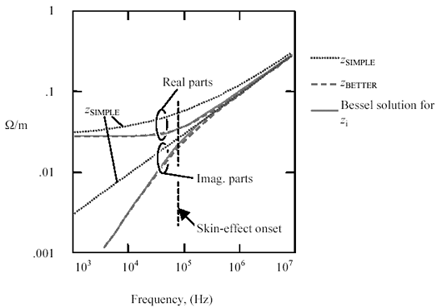
In particular, at w d the real part of z SIMPLE looms far too large, exceeding R DC by 6.02 dB. At that same frequency the real part of z BETTER is only 2.09 dB larger than R DC , much closer to the correct value (according to the Bessel-function solution) of 2.04 dB.
The second problem with z SIMPLE concerns its predicted value of L i at low frequencies. The imaginary part of z SIMPLE should have a positive slope of +20 dB/decade at low frequencies. Instead, it has a slope of only +10 dB/decade, an artifact that effectively predicts infinite inductance at DC.
These shortcomings combine to produce fractional errors in z SIMPLE on the order of 50% at w d , falling off to approximately 10% at frequencies two decades on either side of w d . Don't use z SIMPLE near the transition region. If your simulation operates exclusively at frequencies above w d , then approximation z SIMPLE may be somewhat improved by assuming R DC = 0.
If you require a more accurate approximation, try z BETTER . In the simulation of RG-58/U coaxial cable the peak error in z i induced by the use of z SIMPLE is 56.7%, where the error is expressed as a percentage of z i . The error in z BETTER under the same conditions is only 6.7%. Because the internal impedance z i represents only a part of the overall series impedance z s , calculating the same errors as a fraction of the overall series impedance z s results in values of 25.4% and 1.4% for z SIMPLE and z BETTER , respectively. If you need even better accuracy in the transition region than provided by z BETTER , use a two-dimensional full-wave electromagnetic field solver.
2.8.2 Special Issues Concerning Rectangular Conductors
For rectangular conductors there exist no closed-form solutions for internal inductance. Nor can the internal inductance be evaluated using ordinary quasi-static 2-D calculations, because the phase of the current deep inside the conductor differs substantially from the phase on the surface. This difference in phase introduces new complications into the mathematics of the problem ”complications not handled by commonly available 2-D field simulation software.
Fortunately, the exact value of L i matters little in the computation of many signal-integrity results, because the external inductance L e always exceeds the internal inductance L i for all but the very lowest-impedance configurations. As the frequency rises above w d , the difference becomes even more pronounced so that any error in L i is quickly swamped. The largest simulation errors lie near the skin-effect onset frequency, falling off on either side of the onset. For signal-integrity simulations of transmission lines at reasonable impedances (i.e., L e >> L i ) or at frequencies well above w d , this author uses approximation z BETTER for rectangular conductors.
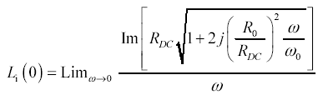
Below the skin-effect onset, the magnitude of the internal inductance L i plays a role in determining the phase delay of the transmission line. For nonround conductors, approximation z BETTER makes some particular assumptions about the low-frequency value of L i . The values of L i implied by the use of approximation z BETTER are found by evaluating Im( z BETTER )/ w in the limit as w 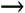 0.
0.
Equation 2.53

The evaluation proceeds by first factoring R DC from under the radical .
Equation 2.54
Take the first two terms in the Taylor's series approximation for 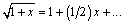
Equation 2.55

Take the imaginary part and simplify the expression.
Equation 2.56
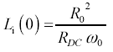
Substitute [2.37] for R DC . Substitute [2.43] for real part of the skin-effect impedance, R , evaluated at frequency w . Assume k a = k r = 1.
Equation 2.57
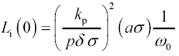
Plug in definition of the skin depth.
Equation 2.58
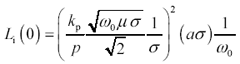
The final result is
Equation 2.59

Table 2.5 lists the low-frequency internal inductance values asserted by approximation z BETTER for various conductor geometries. Please don't make the mistake of assuming these are authoritative values of L i (0) for the listed geometries (except for the round wire, which is exact). These are merely reasonable assumptions made by the approximation Z BETTER .
If you need more accurate models in the vicinity of the skin-effect onset, you should use a 3-D full-wave electromagnetic field solver.
POINTS TO REMEMBER
- Merely adding the DC and AC models of resistance produces substantial errors at frequencies near the onset of the skin effect, and predicts the wrong value of internal inductance.
- The second-order approximation [2.52] better matches both the real and imaginary parts of the skin effect at frequencies near the transition region.
Fundamentals
- Impedance of Linear, Time-Invariant, Lumped-Element Circuits
- Power Ratios
- Rules of Scaling
- The Concept of Resonance
- Extra for Experts: Maximal Linear System Response to a Digital Input
Transmission Line Parameters
- Transmission Line Parameters
- Telegraphers Equations
- Derivation of Telegraphers Equations
- Ideal Transmission Line
- DC Resistance
- DC Conductance
- Skin Effect
- Skin-Effect Inductance
- Modeling Internal Impedance
- Concentric-Ring Skin-Effect Model
- Proximity Effect
- Surface Roughness
- Dielectric Effects
- Impedance in Series with the Return Path
- Slow-Wave Mode On-Chip
Performance Regions
- Performance Regions
- Signal Propagation Model
- Hierarchy of Regions
- Necessary Mathematics: Input Impedance and Transfer Function
- Lumped-Element Region
- RC Region
- LC Region (Constant-Loss Region)
- Skin-Effect Region
- Dielectric Loss Region
- Waveguide Dispersion Region
- Summary of Breakpoints Between Regions
- Equivalence Principle for Transmission Media
- Scaling Copper Transmission Media
- Scaling Multimode Fiber-Optic Cables
- Linear Equalization: Long Backplane Trace Example
- Adaptive Equalization: Accelerant Networks Transceiver
Frequency-Domain Modeling
- Frequency-Domain Modeling
- Going Nonlinear
- Approximations to the Fourier Transform
- Discrete Time Mapping
- Other Limitations of the FFT
- Normalizing the Output of an FFT Routine
- Useful Fourier Transform-Pairs
- Effect of Inadequate Sampling Rate
- Implementation of Frequency-Domain Simulation
- Embellishments
- Checking the Output of Your FFT Routine
Pcb (printed-circuit board) Traces
- Pcb (printed-circuit board) Traces
- Pcb Signal Propagation
- Limits to Attainable Distance
- Pcb Noise and Interference
- Pcb Connectors
- Modeling Vias
- The Future of On-Chip Interconnections
Differential Signaling
- Differential Signaling
- Single-Ended Circuits
- Two-Wire Circuits
- Differential Signaling
- Differential and Common-Mode Voltages and Currents
- Differential and Common-Mode Velocity
- Common-Mode Balance
- Common-Mode Range
- Differential to Common-Mode Conversion
- Differential Impedance
- Pcb Configurations
- Pcb Applications
- Intercabinet Applications
- LVDS Signaling
Generic Building-Cabling Standards
- Generic Building-Cabling Standards
- Generic Cabling Architecture
- SNR Budgeting
- Glossary of Cabling Terms
- Preferred Cable Combinations
- FAQ: Building-Cabling Practices
- Crossover Wiring
- Plenum-Rated Cables
- Laying Cables in an Uncooled Attic Space
- FAQ: Older Cable Types
100-Ohm Balanced Twisted-Pair Cabling
- 100-Ohm Balanced Twisted-Pair Cabling
- UTP Signal Propagation
- UTP Transmission Example: 10BASE-T
- UTP Noise and Interference
- UTP Connectors
- Issues with Screening
- Category-3 UTP at Elevated Temperature
150-Ohm STP-A Cabling
- 150-Ohm STP-A Cabling
- 150- W STP-A Signal Propagation
- 150- W STP-A Noise and Interference
- 150- W STP-A: Skew
- 150- W STP-A: Radiation and Safety
- 150- W STP-A: Comparison with UTP
- 150- W STP-A Connectors
Coaxial Cabling
- Coaxial Cabling
- Coaxial Signal Propagation
- Coaxial Cable Noise and Interference
- Coaxial Cable Connectors
Fiber-Optic Cabling
- Fiber-Optic Cabling
- Making Glass Fiber
- Finished Core Specifications
- Cabling the Fiber
- Wavelengths of Operation
- Multimode Glass Fiber-Optic Cabling
- Single-Mode Fiber-Optic Cabling
Clock Distribution
- Clock Distribution
- Extra Fries, Please
- Arithmetic of Clock Skew
- Clock Repeaters
- Stripline vs. Microstrip Delay
- Importance of Terminating Clock Lines
- Effect of Clock Receiver Thresholds
- Effect of Split Termination
- Intentional Delay Adjustments
- Driving Multiple Loads with Source Termination
- Daisy-Chain Clock Distribution
- The Jitters
- Power Supply Filtering for Clock Sources, Repeaters, and PLL Circuits
- Intentional Clock Modulation
- Reduced-Voltage Signaling
- Controlling Crosstalk on Clock Lines
- Reducing Emissions
Time-Domain Simulation Tools and Methods
- Ringing in a New Era
- Signal Integrity Simulation Process
- The Underlying Simulation Engine
- IBIS (I/O Buffer Information Specification)
- IBIS: History and Future Direction
- IBIS: Issues with Interpolation
- IBIS: Issues with SSO Noise
- Nature of EMC Work
- Power and Ground Resonance
Points to Remember
Appendix A. Building a Signal Integrity Department
Appendix B. Calculation of Loss Slope
Appendix C. Two-Port Analysis
- Appendix C. Two-Port Analysis
- Simple Cases Involving Transmission Lines
- Fully Configured Transmission Line
- Complicated Configurations
Appendix D. Accuracy of Pi Model
Appendix E. erf( )
Notes
EAN: N/A
Pages: 163
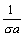
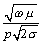
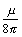

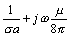
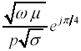
 1. This value may be computed using [2.43] or [2.44].
1. This value may be computed using [2.43] or [2.44].