Stacks and Queues
THE CONCEPT OF STACKS AND QUEUES
There are many applications requiring the use of the data structures stacks and queues. The most striking use of a data structure stack is the runtime stack that a programming language uses to implement a function call and return. Similarly, one of the important uses of a data structure queue is the process queue maintained by the scheduler. Both these data structures are modified versions of the list data structure, so they can be implemented using arrays or linked representation.
STACKS
A stack is simply a list of elements with insertions and deletions permitted at one end—called the stack top. That means that it is possible to remove elements from a stack in reverse order from the insertion of elements into the stack. Thus, a stack data structure exhibits the LIFO (last in first out) property. Push and pop are the operations that are provided for insertion of an element into the stack and the removal of an element from the stack, respectively. Shown in Figure 19.1 are the effects of push and pop operations on the stack.
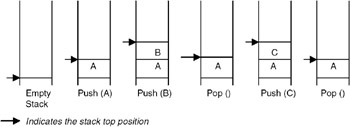
Figure 19.1: Stack operations.
Since a stack is basically a list, it can be implemented by using an array or by using a linked representation.
Array Implementation of a Stack
When an array is used to implement a stack, the push and pop operations are realized by using the operations available on an array. The limitation of an array implementation is that the stack cannot grow and shrink dynamically as per the requirement.
Program
A complete C program to implement a stack using an array appears here:
#include
#define MAX 10 /* The maximum size of the stack */
#include
void push(int stack[], int *top, int value)
{
if(*top < MAX )
{
*top = *top + 1;
stack[*top] = value;
}
else
{
printf("The stack is full can not push a value
");
exit(0);
}
}
void pop(int stack[], int *top, int * value)
{
if(*top >= 0 )
{
*value = stack[*top];
*top = *top - 1;
}
else
{
printf("The stack is empty can not pop a value
");
exit(0);
}
}
void main()
{
int stack[MAX];
int top = -1;
int n,value;
do
{
do
{
printf("Enter the element to be pushed
");
scanf("%d",&value);
push(stack,&top,value);
printf("Enter 1 to continue
");
scanf("%d",&n);
} while(n == 1);
printf("Enter 1 to pop an element
");
scanf("%d",&n);
while( n == 1)
{
pop(stack,&top,&value);
printf("The value poped is %d
",value);
printf("Enter 1 to pop an element
");
scanf("%d",&n);
}
printf("Enter 1 to continue
");
scanf("%d",&n);
} while(n == 1);
}
Example
Enter the element to be pushed
10
Enter 1 to continue
1
Enter the element to be pushed
20
Enter 1 to continue
0
Enter 1 to pop an element
1
The value popped is 20
Enter 1 to pop an element
0
Enter 1 to continue
1
Enter the element to be pushed
40
Enter 1 to continue
1
Enter the element to be pushed
50
Enter 1 to continue
0
Enter 1 to pop an element
1
The value popped is 50
Enter 1 to pop an element
1
The value popped is 40 Enter 1 to pop an element
1
The value popped is 10 Enter 1 to pop an element
0
Enter 1 to continue
0
Implementation of a Stack Using Linked Representation
Initially the list is empty, so the top pointer is NULL. The push function takes a pointer to an existing list as the first parameter and a data value to be pushed as the second parameter, creates a new node by using the data value, and adds it to the top of the existing list. A pop function takes a pointer to an existing list as the first parameter, and a pointer to a data object in which the popped value is to be returned as a second parameter. Thus it retrieves the value of the node pointed to by the top pointer, takes the top point to the next node, and destroys the node that was pointed to by the top.
If this strategy is used for creating a stack with the previously used four data values: 10, 20, 30, and 40, then the stack is created as shown in Figure 19.2.
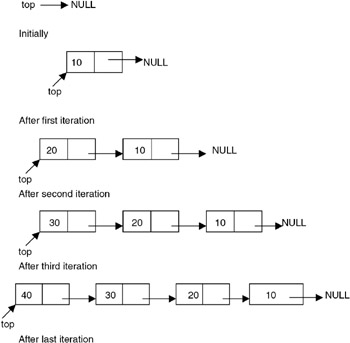
Figure 19.2: Linked stack.
Program
A complete C program for implementation of a stack using the linked list is given here:
# include
# include
struct node
{
int data;
struct node *link;
};
struct node *push(struct node *p, int value)
{
struct node *temp;
temp=(struct node *)malloc(sizeof(struct node));
/* creates new node
using data value
passed as parameter */
if(temp==NULL)
{
printf("No Memory available Error
");
exit(0);
}
temp->data = value;
temp->link = p;
p = temp;
return(p);
}
struct node *pop(struct node *p, int *value)
{
struct node *temp;
if(p==NULL)
{
printf(" The stack is empty can not pop Error
");
exit(0);
}
*value = p->data;
temp = p;
p = p->link;
free(temp);
return(p);
}
void main()
{
struct node *top = NULL;
int n,value;
do
{
do
{
printf("Enter the element to be pushed
");
scanf("%d",&value);
top = push(top,value);
printf("Enter 1 to continue
");
scanf("%d",&n);
} while(n == 1);
printf("Enter 1 to pop an element
");
scanf("%d",&n);
while( n == 1)
{
top = pop(top,&value);
printf("The value poped is %d
",value);
printf("Enter 1 to pop an element
");
scanf("%d",&n);
}
printf("Enter 1 to continue
");
scanf("%d",&n);
} while(n == 1);
}
Example
Input and Output
Enter the element to be pushed
10
Enter 1 to continue
1
Enter the element to be pushed
20
Enter 1 to continue
0
Enter 1 to pop an element
1
The value popped is 20
Enter 1 to pop an element
1
The value poped is 10
Enter 1 to pop an element
0
Enter 1 to continue
1
Enter the element to be pushed
30
Enter 1 to continue
1
Enter the element to be pushed
40
Enter 1 to continue
0
Enter 1 to pop an element
1
The value popped is 40
Enter 1 to pop an element
0
Enter 1 to continue
1
Enter the element to be pushed
50
Enter 1 to continue
0
Enter 1 to pop an element
1
The value popped is 50
Enter 1 to pop an element
1
The value popped is 30
Enter 1 to pop an element
0
Enter 1 to continue
0
APPLICATIONS OF STACKS
Introduction
One of the applications of the stack is in expression evaluation. A complex assignment statement such as a = b + c*d/e–f may be interpreted in many different ways. Therefore, to give a unique meaning, the precedence and associativity rules are used. But still it is difficult to evaluate an expression by computer in its present form, called the infix notation. In infix notation, the binary operator comes in between the operands. A unary operator comes before the operand. To get it evaluated, it is first converted to the postfix form, where the operator comes after the operands. For example, the postfix form for the expression a*(b–c)/d is abc–*d/. A good thing about postfix expressions is that they do not require any precedence rules or parentheses for unique definition. So, evaluation of a postfix expression is possible using a stack-based algorithm.
Program
Convert an infix expression to prefix form.
#include #include #include #define N 80 typedef enum {FALSE, TRUE} bool; #include "stack.h" #include "queue.h" #define NOPS 7 char operators [] = "()^/*+-"; int priorities[] = {4,4,3,2,2,1,1}; char associates[] = " RLLLL"; char t[N]; char *tptr = t; // this is where prefix will be saved. int getIndex( char op ) { /* * returns index of op in operators. */ int i; for( i=0; i
Explanation
- In an infix expression, a binary operator separates its operands (a unary operator precedes its operand). In a postfix expression, the operands of an operator precede the operator. In a prefix expression, the operator precedes its operands. Like postfix, a prefix expression is parenthesis-free, that is, any infix expression can be unambiguously written in its prefix equivalent without the need for parentheses.
- To convert an infix expression to reverse-prefix, it is scanned from right to left. A queue of operands is maintained noting that the order of operands in infix and prefix remains the same. Thus, while scanning the infix expression, whenever an operand is encountered, it is pushed in a queue. If the scanned element is a right parenthesis (‘)’), it is pushed in a stack of operators. If the scanned element is a left parenthesis (‘(‘), the queue of operands is emptied to the prefix output, followed by the popping of all the operators up to, but excluding, a right parenthesis in the operator stack.
- If the scanned element is an arbitrary operator o, then the stack of operators is checked for operators with a greater priority then o. Such operators are popped and written to the prefix output after emptying the operand queue. The operator o is finally pushed to the stack.
- When the scanning of the infix expression is complete, first the operand queue, and then the operator stack, are emptied to the prefix output. Any whitespace in the infix input is ignored. Thus the prefix output can be reversed to get the required prefix expression of the infix input.
Example
If the infix expression is a*b + c/d, then different snapshots of the algorithm, while scanning the expression from right to left, are shown in Table 19.1.
|
STEP |
REMAINING EXPRESSION |
SCANNED ELEMENT |
QUEUE OF OPERANDS |
STACK OF OPERATORS |
PREFIX OUTPUT |
||
|---|---|---|---|---|---|---|---|
|
0 |
a*b+c/d |
nil |
empty |
empty |
nil |
||
|
1 |
a*b+c/ |
d |
d |
empty |
nil |
||
|
2 |
a*b+c |
/ |
d |
/ |
nil |
||
|
3 |
a*b+ |
c |
d c |
/ |
nil |
||
|
4 |
a*b |
+ |
empty |
+ |
dc/ |
||
|
5 |
a* |
b |
b |
+ |
dc/ |
||
|
6 |
a |
* |
b |
* + |
dc/ |
||
|
7 |
nil |
a |
b a |
* + |
dc/ |
||
|
8 |
nil |
nil |
empty |
empty |
dc/ba*+ |
||
The final prefix output that we get is dc/ba*+ whose reverse is +*ab/cd, which is the prefix equivalent of the input infix expression a*b+c*d. Note that all the operands are simply pushed to the queue in steps 1, 3, 5, and 7. In step 2, the operator / is pushed to the empty stack of operators.
In step 4, the operator + is checked against the elements in the stack. Since / (division) has higher priority than + (addition), the queue is emptied to the prefix output (thus we get ‘dc’ as the output) and then the operator / is written (thus we get ‘dc/’ as the output). The operator + is then pushed to the stack. In step 6, the operator * is checked against the stack elements. Since * (multiplication) has a higher priority than + (addition), * is pushed to the stack. Step 8 signifies that all of the infix expression is scanned. Thus, the queue of operands is emptied to the prefix output (to get ‘dc/ba’), followed by the emptying of the stack of operators (to get ‘dc/ba*+’).
Points to remember
- A prefix expression is parenthesis-free.
- To convert an infix expression to the postfix equivalent, it is scanned from right to left. The prefix expression we get is the reverse of the required prefix equivalent.
- Conversion of infix to prefix requires a queue of operands and a stack, as in the conversion of an infix to postfix.
- The order of operands in a prefix expression is the same as that in its infix equivalent.
- If the scanned operator o1 and the operator o2 at the stack top have the same priority, then the associativity of o2 is checked. If o2 is right-associative, it is popped from the stack.
QUEUES
Introduction
A queue is also a list of elements with insertions permitted at one end—called the rear, and deletions permitted from the other end—called the front. This means that the removal of elements from a queue is possible in the same order in which the insertion of elements is made into the queue. Thus, a queue data structure exhibits the FIFO (first in first out) property. insert and delete are the operations that are provided for insertion of elements into the queue and the removal of elements from the queue, respectively. Shown in Figure 19.3 are the effects of insert and delete operations on the queue.
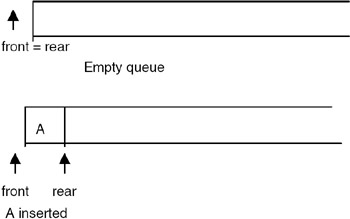
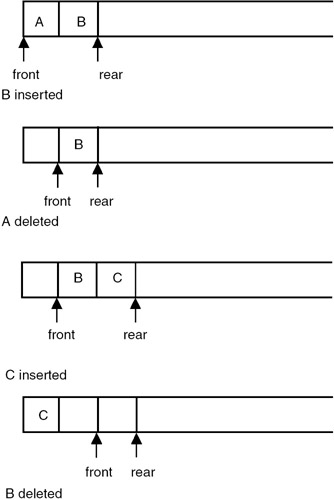Figure 19.3: Operations on a queue.
IMPLEMENTATION OF QUEUES
Introduction
Since a queue is also a list, it can be implemented using an array or it can be implemented using a linked representation.
Array Implementation of a Stack
When an array is used to implement a queue, then the insert and delete operations are realized using the operations available on an array. The limitation of an array implementation is that the queue cannot grow and shrink dynamically as per the requirement.
Program
A complete C program to implement a queue by using an array is shown here:
#include
#define MAX 10 /* The maximum size of the queue */
#include
void insert(int queue[], int *rear, int value)
{
if(*rear < MAX-1)
{
*rear= *rear +1;
queue[*rear] = value;
}
else
{
printf("The queue is full can not insert a value
");
exit(0);
}
}
void delete(int queue[], int *front, int rear, int * value)
{
if(*front == rear)
{
printf("The queue is empty can not delete a value
");
exit(0);
}
*front = *front + 1;
*value = queue[*front];
}
void main()
{
int queue[MAX];
int front,rear;
int n,value;
front=rear=(-1);
do
{
do
{
printf("Enter the element to be inserted
");
scanf("%d",&value);
insert(queue,&rear,value);
printf("Enter 1 to continue
");
scanf("%d",&n);
} while(n == 1);
printf("Enter 1 to delete an element
");
scanf("%d",&n);
while( n == 1)
{
delete(queue,&front,rear,&value);
printf("The value deleted is %d
",value);
printf("Enter 1 to delete an element
");
scanf("%d",&n);
}
printf("Enter 1 to continue
");
scanf("%d",&n);
} while(n == 1);
}
Example
Input and Output
Enter the element to be inserted
10
Enter 1 to continue
1
Enter the element to be inserted
20
Enter 1 to continue
1
Enter the element to be inserted
30
Enter 1 to continue
0
Enter 1 to delete an element
1
The value deleted is 10
Enter 1 to delete an element
1
The value deleted is 20
Enter 1 to delete an element
0
Enter 1 to continue
1
Enter the element to be inserted
40
Enter 1 to continue
1
Enter the element to be inserted
50
Enter 1 to continue
0
Enter 1 to delete an element
1
The value deleted is 30
Enter 1 to delete an element
1
The value deleted is 40
Enter 1 to delete an element
0
Enter 1 to continue
0
CIRCULAR QUEUES
Introduction
The problem with the previous implementation is that the insert function gives a queue-full signal even if a considerable portion is free. This happens because the queue has a tendency to move to the right unless the ‘front’ catches up with the ‘rear’ and both are reset to 0 again (in the delete procedure). To overcome this problem, the elements of the array are required to shift one position left whenever a deletion is made. But this will make the deletion process inefficient. Therefore, an efficient way of overcoming this problem is to consider the array to be circular, as shown in Figure 19.4.
Figure 19.4: Circular queue.
Program
#include
#define MAX 10 /* The maximum size of the queue */
#include
void insert(int queue[], int *rear, int front, int value)
{
*rear= (*rear +1) % MAX;
if(*rear == front)
{
printf("The queue is full can not insert a value
");
exit(0);
}
queue[*rear] = value;
}
void delete(int queue[], int *front, int rear, int * value)
{
if(*front == rear)
{
printf("The queue is empty can not delete a value
");
exit(0);
}
*front = (*front + 1) % MAX;
*value = queue[*front];
}
void main()
{
int queue[MAX];
int front,rear;
int n,value;
front=0; rear=0;
do
{
do
{
printf("Enter the element to be inserted
");
scanf("%d",&value);
insert(queue,&rear,front,value);
printf("Enter 1 to continue
");
scanf("%d",&n);
} while(n == 1);
printf("Enter 1 to delete an element
");
scanf("%d",&n);
while( n == 1)
{
delete(queue,&front,rear,&value);
printf("The value deleted is %d
",value);
printf("Enter 1 to delete an element
");
scanf("%d",&n);
}
printf("Enter 1 to continue
");
scanf("%d",&n);
} while(n == 1);
}
Example
Input and Output
Enter the element to be inserted
10
Enter 1 to continue
1
Enter the element to be inserted
20
Enter 1 to continue
1
Enter the element to be inserted
30
Enter 1 to continue
1
Enter the element to be inserted
40
Enter 1 to continue
1
Enter the element to be inserted
50
Enter 1 to continue
1
Enter the element to be inserted
60
Enter 1 to continue
1
Enter the element to be inserted
70
Enter 1 to continue
1
Enter the element to be inserted
80
Enter 1 to continue
1
Enter the element to be inserted
90
Enter 1 to continue
0
Enter 1 to delete an element
1
The value deleted is 10
Enter 1 to delete an element
1
The value deleted is 20
Enter 1 to delete an element
0
Enter 1 to continue
1
Enter the element to be inserted
100
Enter 1 to continue
1
Enter the element to be inserted
110
Enter 1 to continue
0
Enter 1 to delete an element
1
The value deleted is 30
Enter 1 to delete an element
1
The value deleted is 40
Enter 1 to delete an element
0
Enter 1 to continue
1
Enter the element to be inserted
120
Enter 1 to continue
1
Enter the element to be inserted
130
Enter 1 to continue
0
Enter 1 to delete an element
0
Enter 1 to continue
0
IMPLEMENTATION OF A QUEUE USING LINKED REPRESENTATION
Introduction
Initially, the list is empty, so both the front and rear pointers are NULL. The insert function creates a new node, puts the new data value in it, appends it to an existing list, and makes the rear pointer point to it. A delete function checks whether the queue is empty, and if not, retrieves the data value of the node pointed to by the front, advances the front, and frees the storage of the node whose data value has been retrieved.
If the above strategy is used for creating a queue with four data values —10, 20, 30, and 40, the queue gets created as shown in Figure 19.5.
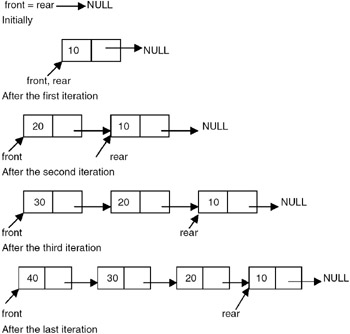
Figure 19.5: Linked queue.
Program
A complete C program for implementation of a stack using the linked list is shown here:
# include
# include
struct node
{
int data;
struct node *link;
};
void insert(struct node **front, struct node **rear, int value)
{
struct node *temp;
temp=(struct node *)malloc(sizeof(struct node));
/* creates new node
using data value
passed as parameter */
if(temp==NULL)
{
printf("No Memory available Error
");
exit(0);
}
temp->data = value;
temp->link=NULL;
if(*rear == NULL)
{
*rear = temp;
*front = *rear;
}
else
{
(*rear)->link = temp;
*rear = temp;
}
}
void delete(struct node **front, struct node **rear, int *value)
{
struct node *temp;
if((*front == *rear) && (*rear == NULL))
{
printf(" The queue is empty cannot delete Error
");
exit(0);
}
*value = (*front)->data;
temp = *front;
*front = (*front)->link;
if(*rear == temp)
*rear = (*rear)->link;
free(temp);
}
void main()
{
struct node *front=NULL,*rear = NULL;
int n,value;
do
{
do
{
printf("Enter the element to be inserted
");
scanf("%d",&value);
insert(&front,&rear,value);
printf("Enter 1 to continue
");
scanf("%d",&n);
} while(n == 1);
printf("Enter 1 to delete an element
");
scanf("%d",&n);
while( n == 1)
{
delete(&front,&rear,&value);
printf("The value deleted is %d
",value);
printf("Enter 1 to delete an element
");
scanf("%d",&n);
}
printf("Enter 1 to continue
");
scanf("%d",&n);
} while(n == 1);
}
Example
Input and Output
Enter the element to be inserted
10
Enter 1 to continue
1
Enter the element to be inserted
20
Enter 1 to continue
1
Enter the element to be inserted
30
Enter 1 to continue
0
Enter 1 to delete an element
1
The value deleted is 10
Enter 1 to delete an element
1
The value deleted is 20
Enter 1 to delete an element
0
Enter 1 to continue
1
Enter the element to be inserted
40
Enter 1 to continue
1
Enter the element to be inserted
50
Enter 1 to continue
0
Enter 1 to delete an element
1
The value deleted is 30
Enter 1 to pop an element
1
The value deleted is 40
Enter 1 to delete an element
1
The value deleted is 50
Enter 1 to delete an element
1
The queue is empty, cannot delete Error
APPLICATIONS OF QUEUES
Introduction
One application of the queue data structure is in the implementation of priority queues required to be maintained by the scheduler of an operating system. It is a queue in which each element has a priority value and the elements are required to be inserted in the queue in decreasing order of priority. This requires a change in the function that is used for insertion of an element into the queue. No change is required in the delete function.
Program
A complete C program implementing a priority queue is shown here:
# include
# include
struct node
{
int data;
int priority;
struct node *link;
};
void insert(struct node **front, struct node **rear, int value, int priority)
{
struct node *temp,*temp1;
temp=(struct node *)malloc(sizeof(struct node));
/* creates new node using data value
passed as parameter */
if(temp==NULL)
{
printf("No Memory available Error
");
exit(0);
}
temp->data = value;
temp->priority = priority;
temp->link=NULL;
if(*rear == NULL) /* This is the first node */
{
*rear = temp;
*front = *rear;
}
else
{
if((*front)->priority < priority)
/* the element to be inserted has
highest priority hence should
be the first element*/
{
temp->link = *front;
*front = temp;
}
else
if( (*rear)->priority > priority)
/* the element to be inserted has
lowest priority hence should
be the last element*/
{
(*rear)->link = temp;
*rear = temp;
}
else
{
temp1 = *front;
while((temp1->link)->priority >= priority)
/* find the position and insert the new element */
temp1=temp1->link;
temp->link = temp1->link;
temp1->link = temp;
}
}
void delete(struct node **front, struct node **rear, int *value, int *priority)
{
struct node *temp;
if((*front == *rear) && (*rear == NULL))
{
printf(" The queue is empty cannot delete Error
");
exit(0);
}
*value = (*front)->data;
*priority = (*front)->priority;
temp = *front;
*front = (*front)->link;
if(*rear == temp)
*rear = (*rear)->link;
free(temp);
}
void main()
{
struct node *front=NULL,*rear = NULL;
int n,value, priority;
do
{
do
{
printf("Enter the element to be inserted and its priority
");
scanf("%d %d",&value,&priority);
insert(&front,&rear,value,priority);
printf("Enter 1 to continue
");
scanf("%d",&n);
} while(n == 1);
printf("Enter 1 to delete an element
");
scanf("%d",&n);
while( n == 1)
{
delete(&front,&rear,&value,&priority);
printf("The value deleted is %d and its priority is %d
",
value,priority);
printf("Enter 1 to delete an element
");
scanf("%d",&n);
}
printf("Enter 1 to delete an element
");
scanf("%d",&n);
} while( n == 1)
}
Example
Input and Output
Enter the element to be inserted and its priority
10 90
Enter 1 to continue
1
Enter the element to be inserted and its priority
5 8
Enter 1 to continue
1
Enter the element to be inserted and its priority
11 60
Enter 1 to continue
1
Enter the element to be inserted and its priority
12 75
Enter 1 to continue
1
Enter the element to be inserted and its priority
13 10
Enter 1 to continue
1
Enter the element to be inserted and its priority
14 6
Enter 1 to continue
0
Enter 1 to delete an element
1
The value deleted is 10 and its priority is 90
Enter 1 to delete an element
1
The value deleted is 12 and its priority is 75
Enter 1 to delete an element
1
The value deleted is 11 and its priority is 60 Enter 1 to delete an element
1
The value deleted is 13 and its priority is 10 Enter 1 to delete an element
1
The value deleted is 5 and its priority is 8
Enter 1 to delete an element
1
The value deleted is 14 and its priority is 6
Enter 1 to delete an element
1
The queue is empty cannot delete Error
Points to Remember
- A stack is basically a list with insertions and deletions permitted from only one end, called the stack-top, so it is a data structure that exhibits the LIFO property.
- The operations that are permitted to manipulate a stack are push and pop.
- One of the important applications of a stack is in the implementation of recursion in the programming language.
- A queue is also a list with insertions permitted from one end, called rear, and deletions permitted from the other end, called front. So it is a data structure that exhibits the FIFO property.
- The operations that are permitted on a queue are insert and delete.
- A circular queue is a queue in which the element next to the last element is the first element.
- When the size of the stack/queue is known beforehand, the array implementation can be used and is more efficient.
- When the size of the stack/queue is not known beforehand, then the linked representation is used. It provides more flexibility.
Exercises
- Write a C program to implement a stack of characters.
- Write a C program to implement a double-ended queue, which is a queue in which insertions and deletions may be performed at either end. Use a linked representation.
Part I - C Language
- Introduction to the C Language
- Data Types
- C Operators
- Control Structures
- The printf Function
- Address and Pointers
- The scanf Function
- Preprocessing
- Arrays
- Function
- Storage of Variables
- Memory Allocation
- Recursion
- Strings
- Structures
- Union
- Files
Part II - Data Structures
Part III - Advanced Problems in Data Structures
EAN: 2147483647
Pages: 232
