Problems in Graphs | Part III - Advanced Problems in Data Structures

Table of contents:

PROBLEM THE DFS METHOD FOR GRAPH TRAVERSAL

Write a function dfs(v) to traverse a graph in a depth-first manner starting from vertex v. Use this function to find connected components in the graph. Modify dfs() to produce a list of newly visited vertices. The graph is represented as an adjacency matrix.

Program

#include #define MAXVERTICES 20 #define MAXEDGES 20 typedef enum {FALSE, TRUE, TRISTATE} bool; struct graph { int matrix[MAXVERTICES][MAXEDGES]; int vertices, edges; }graph; void buildINC( int edges[][MAXEDGES], int nedges ) { /* * fills graph.matrix with information from edges. * graph.edges = nedges. * graph.vertices is maxEntry in edges. */ int i, j; graph.vertices = -1; graph.edges = nedges; // init matrix to FALSE. for( i=0; i graph.vertices ) graph.vertices = edges[i][j]; } graph.vertices++; // no of vertices = maxvertes + 1; } void printINC() { /* * prints graph. */ int i, j; for( i=0; i=0; -i ) if( visited[ adjv[i] ] == FALSE ) dfs( adjv[i], visited ); } void printSetTristate( int *visited ) { /* * prints all vertices of visited which are TRISTATE. * and set them to TRUE. */ int i; for( i=0; i

Explanation

The graph is represented as an incidence matrix. The rows correspond to each vertex and the columns correspond to each edge in the graph. An entry matrix[i][j] is TRUE if edge j contains vertex i, otherwise it is FALSE. For example, if the graph is as follows;

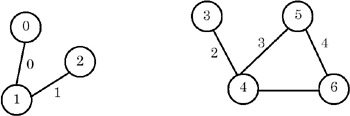
and the edges are numbered as shown, then the incidence matrix for the graph is as shown here:

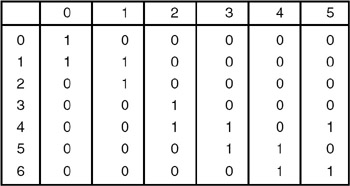
The rows of the incidence matrix are vertices and the columns are edges.
dfs(v) is implemented recursively. A Boolean vector visited[] is maintained, whose all entries are initially FALSE. dfs(v) marks v as visited by making visited[v] = TRUE. It then finds all the adjacent nodes of v and starts dfs() from those nodes which have not yet been visited.
compINC() is a function that finds all the connected components of a graph. It maintains a local copy of the vector visited[] and passes it as a parameter to dfs(v). compINC() passes that vertex as a parameter to dfs(), which is not yet visited. Thus each invoking of dfs() finds one connected component of the graph.
In order to modify dfs() to produce a list of newly visited vertices, we tag the vertices visited using dfs() as TRISTATE. In compINC(), all these TRISTATE vertices will form one connected component. This status is then converted to TRUE. The next invocation of dfs() returns another set of vertices tagged as TRISTATE, which forms another connected component, and so on.

For example, in this graph, first all vertices are tagged as FALSE. After invoking dfs(0), the vertices tagged as TRISTATE are {0, 1, 2}. These are output and their tags are changed from TRISTATE to TRUE. The next invoking of dfs(3) tags vertices {3, 4, 5, 6} as TRISTATE. These are then output and their tags are changed from TRISTATE to TRUE. Since there is no vertex remaining whose tag is FALSE, the algorithm stops.

Points to Remember

All the reachable vertices can be traversed from a source vertex by using the depth-first search.
The data representation (graph in this case) should be such that it should make algorithms operating on the data efficient.
Note how a simple recursive procedure solves the problem of finding all the reachable vertices from a vertex.
Note the use of descriptive words such as FALSE, TRUE, and TRISTATE, rather than integers 0, 1, and 2. It makes the program easily understandable.

PROBLEM CONNECTED COMPONENTS IN A GRAPH

Write a function dfs(v) to traverse a graph in a depth-first manner starting from vertex v. Use this function to find connected components in the graph. Modify dfs() to produce a list of the newly visited vertices. The graph is represented as adjacency lists.

Program

#include #define MAXVERTICES 20 #define MAXEDGES 20 typedef enum {FALSE, TRUE, TRISTATE} bool; typedef struct node node; struct node { int dst; node *next; }; void printGraph( node *graph[], int nvert ) { /* * prints the graph. */ int i, j; for( i=0; inext ) printf( "[%d] ", ptr->dst ); printf( " " ); } } void insertEdge( node **ptr, int dst ) { /* * insert a new node at the start. */ node *newnode = (node *)malloc( sizeof(node) ); newnode->dst = dst; newnode->next = *ptr; *ptr = newnode; } void buildGraph( node *graph[], int edges[2][MAXEDGES], int nedges ) { /* * fills graph as adjacency list from array edges. */ int i; for( i=0; inext ) if( visited[ ptr->dst ] == FALSE ) dfs( ptr->dst, visited, graph ); } void printSetTristate( int *visited, int nvert ) { /* * prints all vertices of visited which are TRISTATE. * and set them to TRUE. */ int i; for( i=0; i

Explanation

The graph is represented as adjacency lists. The graph contains an array of n pointers where n is the number of vertices in the graph. Each entry i in the array contains a list of vertices to which i is connected. For example, if the graph is as follows:

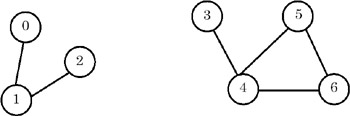
then the adjacency lists for the graph are as shown here:

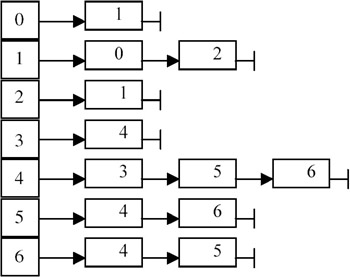
Each node in list i contains a vertex to which i is connected.
dfs(v) is implemented recursively. A Boolean vector visited[] is maintained, whose all entries are initially FALSE. dfs(v) marks v as visited by making visited[v] = TRUE. It then finds all the adjacent nodes of v and starts dfs() from those nodes which have not yet been visited.

For example, if dfs(v) is called with v == 0, it marks 0 and then it traverses the adjacency list graph[0] and calls dfs(1). This marks 1 and traverses the adjacency list graph[1]. But since 0 is already marked, dfs(2) is called. It marks 2 and starts traversal of graph[2]. But since 1 is marked, it returns. All the previous invocations return as there are no nodes being considered in the lists. Thus, the marked vertices are {0, 1, 2}.
compINC() is a function that finds all the connected components of a graph. It maintains a local copy of the vector visited[] and passes it as a parameter to dfs(v). compINC() passes that vertex as a parameter to dfs() which has not yet been visited. Thus each invoking of dfs() finds one connected component of the graph.
In order to modify dfs() to produce a list of newly visited vertices, we tag the vertices visited by using dfs() as TRISTATE. In compINC(), all these TRISTATE vertices will form one connected component. This status is then converted to TRUE. The next invocation of dfs() returns another set of vertices tagged as TRISTATE, which forms another connected component, and so on.

For example, in this graph, first all vertices are tagged as FALSE. After invoking dfs(0), the vertices tagged as TRISTATE are {0, 1, 2}. These are output and their tags are changed from TRISTATE to TRUE. The next invocation of dfs(3) tags vertices {3, 4, 5, 6} as TRISTATE. These are then output and their tags are changed from TRISTATE to TRUE. Since there is no vertex remaining whose tag is FALSE, the algorithm stops.

Points to Remember

All the reachable vertices can be traversed from a source vertex by using the depth-first search.
The data representation (a graph, in this case) should be such that it makes algorithms operating on the data efficient. Being represented as adjacency lists, we could easily traverse the list to get the vertices adjacent to a particular vertex.
Note how a simple recursive procedure solves the problem of finding all the reachable vertices from a vertex.
Note the use of descriptive words such as FALSE, TRUE, and TRISTATE, rather than integers 0, 1, and 2. It makes the program easily understandable.

PROBLEM MINIMUM SPANNING TREE

Write a program to find a minimum spanning tree in a graph.

Program

#include #define MAXVERTICES 10 #define MAXEDGES 20 typedef enum {FALSE, TRUE} bool; int getNVert(int edges[][3], int nedges) { /* * returns no of vertices = maxvertex + 1; */ int nvert = -1; int j; for( j=0; j nvert ) nvert = edges[j][0]; if( edges[j][1] > nvert ) nvert = edges[j][1]; } return ++nvert; // no of vertices = maxvertex + 1; } bool isPresent(int edges[][3], int nedges, int v) { /* * checks whether v has been included in the spanning tree. * thus we see whether there is an edge incident on v which has * a negative cost. negative cost signifies that the edge has been * included in the spanning tree. */ int j; for(j=0; j edges[j][2]) { tv1 = edges[i][0]; tv2 = edges[i][1]; tcost = edges[i][2]; edges[i][0] = edges[j][0]; edges[i][1] = edges[j][1]; edges[i][2] = edges[j][2]; edges[j][0] = tv1; edges[j][1] = tv2; edges[j][2] = tcost; } for(j=0; j

Program Description

A tree consisting solely of edges in a graph G and including all vertices in G is called a spanning tree. A minimum spanning tree of a weighted graph is the spanning tree with the minimum total cost of its edges. Example:
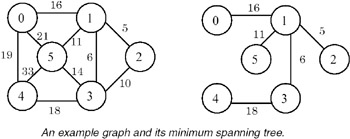
The graph is represented as an array of edges. Each entry in the array is a triplet representing an edge consisting of source vertex, destination vertex, and the cost associated with the edge. The method used in finding a minimum spanning tree is that given by Kruskal. In this approach, a minimum spanning tree T is built edge by edge. Edges are considered for inclusion in T in a non- decreasing order of their costs. An edge is included if it does not form a cycle with the edges already in T. Since graph G is connected, and has n> 0 vertices, exactly n–1 edges will be selected for inclusion in T.

Kruskal's algorithm is as follows:

T={}; // empty set.
while T contains less than n-1 edges and E not empty do
 choose an edge (v, w) from E of lowest cost.
 delete (v, w) from E.
 if (v, w) does not create a cycle in T
 add (v, w) to T.
 else
 discard (v, w).
endwhile.
if T contains less than n-1 edges
 print("no spanning tree exists for this graph.");

In order for the choice of the lowest cost edge from E to become efficient, we sort the edge array over the cost of the edge. To check whether an edge (v, w) forms a cycle, we simply need to check whether both v and w appear in any of the previously added edges in T. We assume that all the costs are positive and we make them negative to signify that the edge has been included in T.

Example:
For the example graph, the run of the algorithm is as follows:

step	edge	cost	action	spanning-tree

0	—	—	—	{}
1	(1, 2)	5	accept	{(1, 2)}
2	(1, 3)	6	accept	{(1, 2), (1, 3)}
3	(2, 3)	10	reject	{(1, 2), (1, 3)}
4	(1, 5)	11	accept	{(1, 2), (1, 3), (1, 5)}
5	(3, 5)	14	reject	{(1, 2), (1, 3), (1, 5)}
6	(0, 1)	16	accept	{(1, 2), (1, 3), (1, 5), (0, 1)}
7	(3, 4)	18	accept	{(1, 2), (1, 3), (1, 5), (0, 1), (3, 4)}

Points to Remember

A minimum spanning tree of a weighted graph G is a tree that consists of edges solely from the edges of G, which covers all the vertices in G, and which has the minimum combined cost of its edges.
The complexity of Kruskal's method used for finding the minimum spanning tree of a graph G is O(e loge), where e is the number of edges in G.
Note that the union and find algorithms for set representation can be used to check for cycle and inclusion of an edge in a set.
There can be multiple minimum spanning trees in a graph.

PROBLEM TOPOLOGICAL SORT

Write a program to find the topological order of a digraph G represented as adjacency lists.

Program

#include 

#define N 11 // no of total vertices in the graph.

typedef enum {FALSE, TRUE} bool;
typedef struct node node;

struct node {
 int count; // for arraynodes : in-degree.
 // for listnodes : vertex no this vertex is connected to.
 // if this node is out of graph : -1.
 // if this has 0 indegree then it occurs in zerolist.
 node *next;
};
node graph[N];
node *zerolist;

void addToZerolist( int v ) {
 /*
 * adds v to zerolist as v has 0 predecessors.
 */
 node *ptr = (node *)malloc( sizeof(node) );
 ptr->count = v;
 ptr->next = zerolist;
 zerolist = ptr;
}

void buildGraph( int a[][2], int edges ) {
 /*
 * fills global graph with input given in a.
 * a[i][0] is src vertex and a[i][1] is dst vertex.
 */
 int i;

 // init graph.
 for( i=0; icount = a[i][1];
 ptr->next = graph[ a[i][0] ].next;
 graph[ a[i][0] ].next = ptr;
 // increase indegree of dst.
 graph[ a[i][1] ].count++;
 }

 // now create list of zero predecessors.
 zerolist = NULL; // list of vertices having 0 predecessors.
 for( i=0; inext )
 printf( "%d ", ptr->count );
 printf( "
" );
 }
 printf( "zerolist: " );
 for( ptr=zerolist; ptr; ptr=ptr->next )
 printf( "%d ", ptr->count );
 printf( "
" );
}

int getZeroVertex() {
 /*
 * returns the vertex with zero predecessors.
 * if no such vertex then returns -1.
 */
 int v;
 node *ptr;

 if( zerolist == NULL )
 return -1;
 ptr = zerolist;
 v = ptr->count;
 zerolist = zerolist->next;
 free(ptr);

 return v;
}

void removeVertex( int v ) {
 /*
 * deletes vertex v and its outgoing edges from global graph.
 */
 node *ptr;
 graph[v].count = -1;
 // free the list graph[v].next.
 for( ptr=graph[v].next; ptr; ptr=ptr->next ) {
 if( graph[ ptr->count ].count > 0 ) // normal nodes.
 graph[ ptr->count ].count-;
if( graph[ ptr->count ].count == 0 ) // this is NOT else of above if.
 addToZerolist( ptr->count );
 }
}

void topsort( int nvert ) {
 /*
 * finds recursively topological order of global graph.
 * nvert vertices of graph are needed to be ordered.
 */
 int v;

 if( nvert > 0 ) {
 v = getZeroVertex();
 if( v == -1 ) { // no such vertex.
 fprintf( stderr, "graph contains a cycle.
" );
 return;
 }
 printf( "%d.
", v );
 removeVertex(v);
 topsort( nvert-1 );
 }
}

int main() {
 int a[][2] = {
 {0,1},
 {0,3},
 {0,2},
 {1,4},
 {2,4},
 {2,5},
 {3,4},
 {3,5}
 };
 buildGraph( a, 8 );
 printGraph();
 topsort(N);
}

Explanation

A linear ordering of vertices of a digraph G, with the property that if i is a predecessor of j, then i precedes j in the linear ordering, is called a topological order of G.
The digraph G is maintained as adjacency lists. In this representation, G is an array graph[0…n–1], where each element graph[i] is a linked list of vertices to which vertex i is connected, and n is the number of vertices in G.

We also maintain a zerolist, which is a list of vertices that have zero predecessors. The necessity for this list will be clear from an algorithm for a topological sort, as follows:

 topsort(n) {
 if( n > 0 ) {
 if every vertex has a predecessor then
 error( "graph contains a cycle." ).
 pick a vertex v that has no predecessors. //
getZeroVertex()
 output v.
 delete v and all the edges leading out of v in the graph. // removeVertex()
 topsort(n-1).
 }
}

The algorithm topsort() is tail-recursive. From zerolist, it removes a vertex v containing zero predecessors, and outputs it. This vertex v either has no predecessors in G, or all its predecessors have already been output. Thus all the vertices in zerolist are candidates for the next output. After v is output, all the vertices to which v points may become the candidates for the next output. Thus we remove all the edges starting from v and rerun topsort() over the remaining vertices.
Example: Let the digraph be as shown here.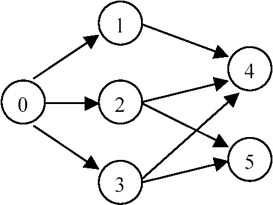

click to expand

Step	Zerolist	Output

0	{0}	nil
1	{1, 2, 3}	0
2	{2, 3}	1
3	{3}	2
4	{4,5}	3
5	{5}	4
6	{}	5

Points to Remember

A linear ordering of vertices of a digraph G, with the property that if i is a predecessor of j, then i precedes j in the linear ordering, is called the topological order of G.
The complexity of topological order is O(n+e) where n is the number of vertices and e is the number of edges in the digraph.
Removal of an edge results in a decrease in the predecessor count of the destination vertex. If this count reaches 0, the vertex should be inserted in the zerolist.
By maintaining a list of vertices with zero predecessors, the computing time of the algorithm decreases.

PROBLEM FINDING THE SHORTEST PATH BY USING AN ADJACENCY MATRIX

Given a digraph represented as an adjacency matrix, find the shortest path from a vertex v to all the other vertices in the graph.

Program

#include #define MAXINT 99999 #define MAXVERTICES 10 typedef enum {FALSE, TRUE} bool; void print( int cost[][MAXVERTICES], int nvert ) { /* * prints cost matrix. */ int i, j; for( i=0; i

Explanation

The digraph is represented as an adjacency matrix. The size of the matrix is N×N where N is the number of vertices in the digraph. An entry matrix[i][j] specifies the cost of the directed edge from vertex i to vertex j. If such an edge does not exist, then the cost is set to MAXINT. All diagonal entries of the matrix matrix[i][i] are set to 0.
The function sssp(v, cost, dist, nvert ) implements the single-source- shortest-path algorithm to find the shortest path from a vertex v in a digraph that is represented as an adjacency matrix cost. nvert is the number of vertices in the digraph and dist is the vector that will finally contain the output. Thus an entry dist[i] will be the minimum distance of vertex i from vertex v.

The function uses a vector s[] of Boolean to represent the status of each vertex: whether processed or not. It is initialized to FALSE. s[v] is marked, meaning it is processed. dist[v] is set to 0. Then the function chooses a vertex u that is yet to be processed and which is at a minimum distance from v. Vertex u is marked as processed. It then processes vector dist[], which may get updated because of the addition of u. The function checks whether dist[u]+cost[u][w] < dist[w] for each yet-to-be-processed node w in the digraph. If it is, then dist[w] is updated as dist[u]+cost[u][w]. When all the vertices are processed, dist[] contains the required result. Example:

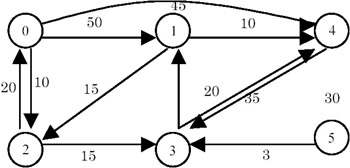
click to expand

Let v=0. Then, different steps in the run of the algorithm are as follows:

M signifies MAXINT, which means that the vertex cannot be reached from v.


step	u	dist





0	nil	0 50 10 M 45 M

1	2	0 50 10 35 45 M

2	3	0 45 10 35 45 M

3	1	0 45 10 35 45 M

4	4	0 45 10 35 45 M

5	5	0 45 10 35 45 M

Points to Remember

The complexity of the sssp() is O(N^2) where N is the number of vertices in the digraph.
The constant of proportionality of the complexity of choose() may be improved by using a list of yet-to-be-processed vertices.
Representing the digraph as an adjacency matrix makes the retrieval of the cost of an edge O(1).

PROBLEM FINDING THE SHORTEST PATH BY USING AN ADJACENCY LIST

Rewrite the function sssp() for finding the shortest path, such that the digraph is represented by its adjacency lists instead of the adjacency matrix. Also, instead of maintaining set S of vertices to which the shortest paths have already been found, the set V(G)–S is represented by using a linked list where V(G) is the set of vertices in digraph G.

Program

#include #define MAXINT 99999 #define MAXVERTICES 10 typedef struct node node; typedef struct setnode setnode; typedef enum {FALSE, TRUE} bool; struct node { int dst; int cost; node *next; }; struct setnode { int v; setnode *next; }; void printGraph( node *cost[], int nvert ) { /* * prints the graph. */ int i, j; for( i=0; inext ) printf( "[%d,%d] ", ptr->dst, ptr->cost ); printf( " " ); } } void insertEdge( node **ptr, int dst, int cost ) { /* * insert a new node at the start. */ node *newnode = (node *)malloc( sizeof(node) ); newnode->dst = dst; newnode->cost = cost; newnode->next = *ptr; *ptr = newnode; } void buildGraph( node *cost[], int costnew[][3], int nedges ) { /* * fills cost as adjacency list from array costnew. */ int i; for( i=0; inext; ptr; ptr=ptr->next ) if( dist[ptr->v] <= mindist ) u=ptr->v, mindist=dist[ptr->v]; return u; } int getCost( node **cost, int src, int dst ) { /* * return cost of edge from src to dst. */ node *ptr; for( ptr=cost[src]; ptr; ptr=ptr->next ) if( ptr->dst == dst ) return ptr->cost; return MAXINT; } void removeFromSet( setnode *s, int v ) { /* * remove vertex v from set s. */ setnode *prev, *ptr; for( prev=s, ptr=prev->next; ptr; prev=ptr, ptr=ptr->next ) if( ptr->v == v ) { prev->next = ptr->next; free(ptr); return; } // v does NOT exist in the set. } void insertIntoSet( setnode *s, int v ) { /* * add vertex v to the set s. */ setnode *ptr = (setnode *)malloc( sizeof(setnode) ); ptr->v = v; ptr->next = s->next; s->next = ptr; } bool isInSet( setnode *s, int v ) { /* * returns TRUE if vertex v is in set s. */ setnode *ptr; for( ptr=s->next; ptr; ptr=ptr->next ) if( ptr->v == v ) return TRUE; return FALSE; } void sssp( int v, node **cost, int dist[], int nvert ) { /* * finds shortest path from v to all other vertices. * cost is the cost adjacency list. * dist is the vector in which output will be written. * nvert is no of vertices in the graph. */ setnode s; // list of vertices yet to be considered. int i, u, num, w; node *ptr; for( i=0; inext ) dist[ptr->dst] = ptr->cost; removeFromSet( &s, v ); dist[v] = 0; num = 1; while( num < nvert-1 ) { u = choose( dist, &s ); removeFromSet( &s, u ); num++; for( w=0; w

Explanation

Cost is maintained as an array containing adjacency lists for each vertex in the digraph. The function buildGraph() fills this array. An adjacency list for a vertex is a linked list where each node contains the vertex, the cost of the corresponding edge, and a pointer to the next node.

For example, consider the following graph:

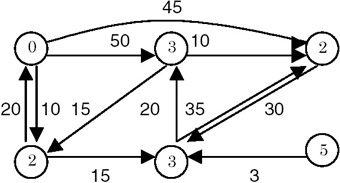
The adjacency lists are maintained as follows:

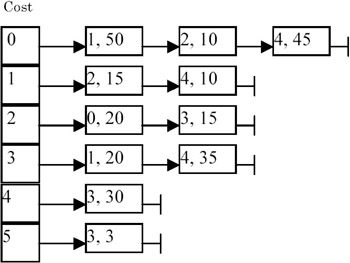
Note that each node contains a pair of integers, (vertex, cost).
The function sssp() remains nearly the same except getting the cost of an edge and accesses the set S. The cost of an edge can be retrieved using the function getCost(). It needs O(n) traversal of the adjacency list corresponding to the source vertex of the edge, where n is the number of nodes in the list. In the cost matrix-based algorithm, this was O(1). Removal of a vertex (removeFromSet()) from the list requires O(n) time. This time was also constant earlier as we flagged the vertex as FALSE. Furthermore, earlier we could check the status of a vertex to be TRUE or FALSE using s[i], but now the function isInSet() needs to traverse the list s to see whether the node has been processed or NOT. This makes it O(n). However, the function choose(), which was earlier O(n), now becomes O(1), as we need to remove only the first element from the list s.
The overall complexity of sssp() increases from O(n^2) to O(n^3) as getCost() and isInSet() become O(n), where n is the number of vertices in the digraph.

Points to Remember

Note how the change in the data structures affected the algorithm efficiency.
In order to make choose() O(1), we had to make removeFromSet() and isInSet() O(n). This trade-off should be studied carefully before implementation.
The change from an adjacency matrix to adjacency lists may reduce some space, but it increases complexity of the function getCost().

PROBLEM THE M SHORTEST PATH

Write a function mshortest( cost, src, dst, m ) that finds m shortest paths 7(if any exist) from src to dst in a digraph represented by its cost adjacency matrix cost.

Program

#include #define M 8 #define MAXVERTICES 10 #define MAXINT 99999 typedef struct node node; typedef struct ansnode ansnode; typedef enum {FALSE, TRUE} bool; struct node { int src; // for head node: this is cost of the edges in the list. int dst; int dummy; // used for temporarily saving the cost of this edge. node *next; }; struct ansnode { node path; node inedges, exedges; }; ansnode answers[M]; int indexans; // no of paths generated so far: >=0 & <= M. void init() { /* * some initialization. */ int i; for( i=0; ipath.src=0; // this is combined cost of the edges in this list. a->path.next = NULL; a->inedges.next = a->exedges.next = NULL; } indexans = 0; } void pushFront( node *edges, int src, int dst ) { /* * adds a new node containing (src,dst) at start of edges. */ node *ptr = (node *)malloc( sizeof(node) ); ptr->src=src; ptr->dst = dst; ptr->next = edges->next; edges->next = ptr; } void pushBack( node *edges, int src, int dst ) { /* * adds a new node containing (src,dst) at end of edges. */ node *ptr; for( ptr=edges; ptr->next; ptr=ptr->next ) ; // (src,dst) should be inserted after ptr; pushFront( ptr, src, dst ); // another hack! } void popFront( node *edges, int *src, int *dst ) { /* * remove a node from start of edges. */ node *ptr = edges->next; if( ptr == NULL ) { *src=*dst = -1; return; } *src=ptr->src; *dst = ptr->dst; edges->next = ptr->next; free(ptr); } int choose( int dist[], bool s[], int nvert ) { /* * returns vertex u such that: * dist[u] = min{ dist[w] } where s[w] == FALSE. */ int i; int u=-1; int mindist = MAXINT; for( i=0; inext; ptr; ptr=ptr->next ) printf( "(%d,%d) ", ptr->src, ptr->dst ); printf( " " ); } node *revList( node *list ) { /* * returns reverse of list: modifies list. */ node *ptr=list->next, *temp, *prev=NULL; for( ; ptr; prev=ptr, ptr=temp ) { temp = ptr->next; ptr->next = prev; } list->next = prev; return list; } int getInsertIndex( node *answer, int start ) { /* * returns index in answers where answer can be inserted. * uses binsrch. */ int mid, end=indexans-1; int midcost=-1, anscost=answer->src; while( start <= end ) { mid = (start+end)/2; midcost = answers[mid].path.src; if( midcost == anscost ) return mid; else if( midcost < anscost ) start = mid+1; else end = mid-1; } if( midcost == -1 ) return start; if( midcost < anscost ) return mid+1; else return mid; } void shiftInsert( int index ) { /* * shifts answers[index..indexans-1] by one down. */ int i; for( i=index; i= MAXINT. */ int index; if( answer->src >= MAXINT ) // path length is infinite. return; index = getInsertIndex( answer, start ); shiftInsert( index ); answers[index].path = *answer; answers[index].inedges = *inedges; answers[index].exedges = *exedges; printf( "______%d cost=%d. ", index, answers[index].path.src ); printList( "____________inedges: ", inedges ); printList( "____________exedges: ", exedges ); indexans++; } node *copied( node *edges ) { /* * return a copy of the list of edges. */ node *ret = (node *)malloc( sizeof(node) ); node *retptr = ret; node *ptr; ret->src=edges->src; ret->next = NULL; for( ptr=edges->next; ptr; ptr=ptr->next ) { retptr->next = (node *)malloc( sizeof(node) ); retptr = retptr->next; retptr->src=ptr->src; retptr->dst = ptr->dst; retptr->next = NULL; } return ret; } void findDstSrc( node *edges, int *dst1, int *src2, int dst ) { /* * returns the first src and last dst of the path ptr. */ node *ptr = edges->next; if( ptr == NULL ) { *dst1 = *src2 = dst; return; } *dst1 = ptr->src; for( ; ptr->next; ptr=ptr->next ) ; *src2 = ptr->dst; } void attachPaths( node *path1, node *inedges, node *path2 ) { /* * path1 = path2+inedges+path1; */ node *ptr; for( ptr=inedges; ptr->next; ptr=ptr->next ) ; ptr->next = path1->next; if( path2 != NULL ) { for( ptr=path2; ptr->next; ptr=ptr->next ) ; ptr->next = inedges->next; path1->next = path2->next; path1->src += path2->src; } else path1->next = inedges->next; path1->src += inedges->src; } node *advanceByInc( node *path, node *inedges ) { /* * return a ptr to the first edge in path which is not in inedges. * simply traverse no of nodes in path equal to that in inedges and return * the next pointer. */ node *ptrpath, *ptrin; for( ptrpath=path->next, ptrin=inedges->next; ptrin; ptrpath=ptrpath->next, ptrin=ptrin->next ) ; return ptrpath; } node *sssp( int cost[][MAXVERTICES], int v, int finalv, int nvert ) { /* * finds shortest path from v to all other vertices and thus to finalv. * cost is the cost matrix. * nvert is no of vertices in the graph. * returns the shortest path. */ bool s[MAXVERTICES]; int i, u, num, w; int spath[MAXVERTICES]; int dist[MAXVERTICES]; node *newpath = (node *)malloc( sizeof(node) ); int src, dst; printf( "solving sssp(%d,%d). ", v, finalv ); newpath->next = NULL; for( i=0; isrc=dist[finalv]; // cost of this path. printf( ". " ); return newpath; } void solveshortest( int index, int cost[][MAXVERTICES], int src, int dst, int nvert ) { /* * driver for sssp(). * sets constraints for the new path. The constraints are * inclusion and exclusion of some edges. * exclusion is done by temporarily making entry cost[i][j] equal to 0 * and then restoring it after sssp(). * inclusion of some path is carried out by calling sssp() twice with the included * path removed. The two paths and the inclusion list together contain the new * shortest path. * the global array of answers is updated as new paths are being calculated. */ node *path = &answers[index].path; node *inedges = &answers[index].inedges; node *exedges = &answers[index].exedges; node *ptr; for( ptr=exedges->next; ptr; ptr=ptr->next ) {// for each exclusion edge. ptr->dummy = cost[ptr->src][ptr->dst]; // saving. cost[ptr->src][ptr->dst] = MAXINT; } ptr = advanceByInc( path, inedges ); for( ; ptr; ptr=ptr->next ) { // for each edge. int dummy1, dummy2; int dst1, src2; node *path1, *path2=NULL; printList( "path: ", path ); printList( "inedges: ", inedges ); printList( "exedges: ", exedges ); // exclusion edges. printf( "exedge=(%d,%d). ", ptr->src, ptr->dst ); pushFront( exedges, ptr->src, ptr->dst ); exedges->next->dummy = cost[ptr->src][ptr->dst]; // saving. cost[ptr->src][ptr->dst] = MAXINT; // temporarily removed. // inclusion edges. findDstSrc( inedges, &dst1, &src2, dst ); printf( "inedges: dst1=%d, src2=%d. ", dst1, src2 ); path1 = sssp( cost, src, dst1, nvert ); if( src2 != dst ) path2 = sssp( cost, src2, dst, nvert ); attachPaths( path1, revList(copied(inedges)), path2 ); printList( "attachpath: ", path1 ); insertAnswer( path1, copied(inedges), copied(exedges), index+1 ); // now restore the cost matrix. cost[ptr->src][ptr->dst] = exedges->next->dummy; // remove the exclusion edge. popFront( exedges, &dummy1, &dummy2 ); // update inclusion list with that edge. pushFront( inedges, dummy1, dummy2 ); inedges->src += cost[dummy1][dummy2]; } for( ptr=exedges->next; ptr; ptr=ptr->next ) // for each exclusion edge. cost[ptr->src][ptr->dst] = ptr->dummy; } void mshortest( int cost[][MAXVERTICES], int src, int dst, int nvert ) { /* * finds m shortest paths between src and dst. */ int i=0; node *inedges = (node *)malloc( sizeof(node) ); node *exedges = (node *)malloc( sizeof(node) ); node *newpath = sssp( cost, src, dst, nvert ); inedges->src=exedges->src=0; inedges->next = exedges->next = NULL; insertAnswer( newpath, inedges, exedges, i ); while( i

Explanation

The digraph G is maintained as its cost adjacency matrix. cost[i][i] = 0 and cost[i][j] = MAXINT for i != j, and if there is no edge from i to j.
We assume that every edge has a positive cost. Let p1 = v0, v1, …, vk be the shortest path from src to dst. If P is the set of all simple src-to-dst paths in G, then it is easy to see that every path in P-{p1} differs from p1 in exactly one of the following k ways.
2. It contains the edges (v1, v2), …, (vk–1, vk) but not (v0, v1).
4. It contains the edges (v2, v3), …, (vk–1, vk) but not (v1, v2).
  - … …
  - (k) It does not contain the edge (vk–1, vk).
Thus we see that if we put constraints on a shortest path as for the aforementioned k conditions, then we get more next-shortest paths satisfying different constraints. These constraints either require certain edges to be included or excluded from the original shortest path as just given.
The algorithm mshortest() is as follows:
```
Q = {(shortest src-to-dst-path, phi)} // phi denotes an empty set.
for i = 1 to m do // generate m shortest paths.
```
Let (p,C) be the tuple in Q such that path p is of minimal length with set of constraints c.
Output path p.
Delete path p from Q.
Determine the shortest paths in G under the constraints C and the additional constraints imposed for the new path being generated as described previously.
Add these shortest paths together with their constraints to Q.
Q is a set of (p, C) pairs where p is the shortest path generated after imposing constraints C. Initially, we find the shortest path from src to dst under no constraints. We then generate m paths in a loop. Inside the loop, we select from Q that (p, C) pair that has the minimum path length. After outputting, we remove the pair from Q. We then find the next shortest paths after imposing the constraints on C and additional constraints by removing an edge from the exclusion-list of edges, and adding that edge to the inclusion list. We also add the next edge of the path to the exclusion list. Thus we form a new set of constraints. We add the shortest paths generated along with the new constraints to the set Q and reiterate.
Use the function sssp() to find a single-source shortest path. Make minor modifications to the function to follow the constraints and exclusion of certain edges. Exclusion is carried out by temporarily removing that edge's cost from the cost matrix and restoring the cost after running sssp() over cost. Inclusion of consecutive edges is carried out by calling sssp() twice, once for the path between the first vertex of the shortest path and before the first vertex in the inclusion list, and then for the path between the last vertex of the included path and the last vertex of the shortest path.

For example, if the shortest path is v0 v1 v2 v3 v5, and the inclusion list is (v2 v3), then sssp() is called for the path v0 v1 v2, and then for the path v3 v5. The new shortest path generated is returned by sssp(). This new path, along with its constraints and cost, is added to a global array[M] of answers sorted on the cost of the path. A binary search is used to get the index (getInsertIndex()) where the new path should be added. Insertion into the array at position i requires shifting of the elements from i forward by one position (shiftInsert()).

Example:

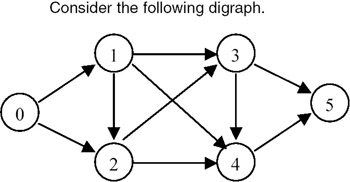
click to expand

The shortest paths generated for the above graph for M == 8 are shown here:

shortest path	cost	included edges	excluded edges	new path

v0 v2 v4 v5	8	none	none.
		none	(v4 v5)	v0 v2 v3 v5 = 9
		(v4 v5)	(v2 v4)	v0 v1 v4 v5 = 12
		(v2 v4) (v4 v5)	(v0 v2)	v0 v1 v2 v4 v5 = 14
v0 v2 v3 v5	9	none	(v4 v5).
		none	(v3 v5) (v4 v5)	infinity
		(v3 v5)	(v2 v3) (v4 v5)	v0 v1 v3 v5 = 13
		(v2 v3) (v3 v5)	(v0 v2) (v4 v5)	v0 v1 v2 v3 v5 = 15
v0 v1 v4 v5	12	(v4 v5)	(v2 v4).
		(v4 v5)	(v1 v4) (v2 v4)	v0 v2 v3 v4 v5 = 16
		(v1 v4) (v4 v5)	(v0 v1) (v2 v4)	infinity
v0 v1 v3 v5	13	(v3 v5)	(v2 v3) (v4 v5)
		(v3 v5)	(v1 v3) (v2 v3) (v4 v5)	infinity
		(v1 v3) (v3 v5)	(v0 v1) (v2 v3) (v4 v5)	infinity
v0 v1 v2 v4 v5	14	(v2 v4) (v4 v5)	(v0 v2)
		(v2 v4) (v4 v5)	(v1 v2) (v0 v2)	infinity
		(v1 v2) (v2 v4) (v4 v5)	(v0 v1) (v0 v2)	nfinity
v0 v1 v2 v3 v5	15	(v2 v3) (v3 v5)		(v0 v2) (v4 v5)
		(v2 v3) (v3 v5)	(v1 v2) (v0 v2) (v4 v5)	infinity
		(v1 v2) (v2 v3) (v3 v5)	(v0 v1) (v0 v2) (v4 v5)	infinity
v0 v2 v3 v4 v5	16	(v4 v5)	(v1 v4) (v2 v4)
		(v4 v5)	(v3 v4) (v1 v4) (v2 v4)	infinity
		(v3 v4) (v4 v5)	(v2 v3) (v1 v4) (v2 v4)	v0 v1 v3 v4 v5 = 20
		(v2 v3) (v3 v4) (v4 v5)	(v0 v2) (v1 v4) (v2 v4)	v0 v1 v2 v3 v4 v5 = 22

Points to Remember

The complexity of mshortest() is O(mn^3), where m is the number of shortest paths generated, and n is the number of vertices in the digraph.
Note how we reused the single-source-shortest-path algorithm with some modifications in mshortest(). This not only eased programming but also simplified the analysis.
Maintaining a reverse list of edges helps in updating the exclusion and inclusion lists easily.

PROBLEM THE ALL COST SHORTEST PATH

Write a function allCosts() to find the shortest path between any two vertices in a digraph.

Program

#include #define MAXINT 99999 #define MAXVERTICES 10 typedef enum {FALSE, TRUE} bool; void print( int cost[][MAXVERTICES], int nvert ) { /* * prints the cost matrix. */ int i, j; for( i=0; i

Explanation

One way to solve the all-costs shortest path problem is to apply the algorithm of shortest path sssp() n times for each vertex in the digraph G. The complexity would be O(n^3). For the all-costs problem, we can obtain a conceptually simpler algorithm that will work even if some edges in G have negative weights, as long as G has no cycles with negative lengths. The computing time will still be O(n^3), although the constant factor will be smaller.
The digraph G is represented as a cost adjacency matrix with cost[i][i] = 0 and cost[i][j] = MAXINT, in case edge , i != j is not in G.
We define Ak[i][j] to be the shortest path from i to j going through no intermediate vertex of index greater than k. Then, An[i][j] will be the cost of the shortest i to j path in G, since G contains no vertex with an index greater than n. A0[i][j] is cost[i][j].
The basic idea in the algorithm is to successively generate matrices A0, A1, …, An. If we have already generated A(k–1), then we may generate Ak by realizing that for any pair of vertices i, j either:
- the shortest path from i to j going through no vertex with index greater than k does not go through the vertex with index k, and so its cost is A(k−1)[i][j]; or
- the shortest such path does go through vertex k. Such a path consists of a path from i to k and another one from k to j. These paths must be the shortest paths from i to k and from k to j going through no vertex with index greater than k–1, and so their costs are A(k–1)[i][k] and A(k–1)[k][j].
Note that this is true only if G has no cycle with negative length containing vertex k. If this is not true, then the shortest i to j path going through no vertices of index greater than k may make several cycles from k to k, and thus have a length substantially less than A(k–1)[i][k]+A(k–1)[k][j]. So, we have the following formulas:
```
Ak[i][j] = min{ A(k-1)[i][j], A(k-1)[i][k]+A(k-1)[k][j] },
k > 0
```
and
```
A0[i][j] = cost[i][j]
```
Example: Let the graph be as shown here.

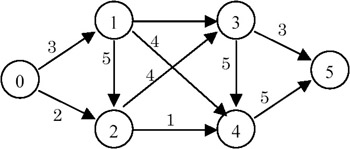
Here, n = 6. The values of Ak, 0<=k<6 are shown next. M signifies MAXINT.

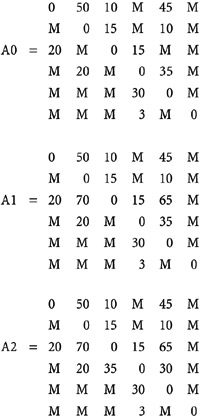
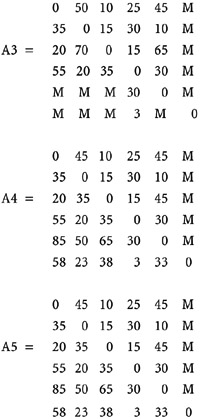
An entry in A5[i][j] gives the minimum path length from vertex i to j.

Points to Remember

The complexity of the algorithm allCosts() is O(n^3).
Different options should be considered before implementation, as we did for this problem. This can result not only in getting an efficient algorithm but also in effectively handling special cases.
See how the problem of size k is recursively defined in terms of a problem of size k–1.

Part I - C Language

Part II - Data Structures

Part III - Advanced Problems in Data Structures