Scaling Copper Transmission Media

Lengthening a transmission line increases its delay while reducing its bandwidth. These two properties are inextricably interrelated. Longer almost always means slower .

Let me pause here to explain that I am writing to you about the optimal use of transmission lines ” specifically , the use of properly terminated transmission lines with drivers that put out clean, fast, full- sized signals and receivers that do not excessively load the far-end terminus of the line. In that case the behavior of the transmission line is governed by its propagation coefficient [3.13]. This coefficient prescribes the attenuation at each frequency in units of dB per meter (or nepers per meter). The overall attenuation of such a physical link scales linearly with distance.

For example, suppose you have one transmission line that has an attenuation of 3 dB at 100 MHz. A second line of twice the length (but otherwise the same) would have precisely 6 dB of attenuation at 100 MHz. Doubling the length doubles the attenuation.

Any exaggeration of the attenuation (by lengthening or any other method) must necessarily lower the 3-dB point. This happens because the attenuation function for real-world transmission lines is always monotonic and decreasing . Increasing the length always reduces the bandwidth .

For robust performance on unequalized receivers with binary data, one normally requires that the 3-dB bandwidth of the transmission media exceed 70% of the bit rate; in this case, increasing the length reduces not only the bandwidth but also the maximum rate of digital transmission that can occur over that transmission system.

If you know the slope of the attenuation function, you can predict the precise relation between the maximum communication rate and distance. Here nature helps us in a profound way: Almost all practical transmission lines have about the same shape to their attenuation function. Most transmission lines used for high-speed digital work display a smooth, rounded knee in their attenuation function, with a profile something like this:

Equation 3.149

 

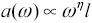
where	a is the attenuation in decibels,
	the constant of proportionality depends on the materials and geometry of the cabling,
	w is the frequency of operation, rad/s,
	h is a slowly varying constant between 1/2 and 1, and
	l is the length of the transmission line, m.

A value of h = 1/2 is typical for transmission lines that are limited primarily by the skin effect. Good examples of skin-effect-limited media would include any of the transmission lines in Figure 3.1 taken over the frequency range from 10 to 1000 MHz.

In the skin-effect-limited range the w 1/2 dependence creates an interesting property of scaling: Doubling the length but cutting the frequency by 1/4 produces precisely the same attenuation. In the time domain,

for skin-effect-limited media, doubling the length while slowing down to 1/4 the bit rate produces the same eye pattern .

Horrible, isn't it! The penalty for doubling the line length is a reduction in bandwidth by a factor of four.

Turn that around the other way and you see the other side: Cutting the length in half speeds up the system by a factor of four. This is what made 10BASE-T Ethernet so popular. At one time, prevailing wisdom suggested that telephone-style unshielded twisted-pair cabling had an inherent bandwidth of only 3KHz to 4 KHz. This reasoning was based on an assumption of length, namely, that every system had to be able to operate at distances sufficient to reach the nearest telephone central office, which could be as much as 5000 meters distant . Once people in the LAN business recognized that interoffice LAN communications needed only to go 100 meters, the bandwidth assumption could be boosted by a factor of (5000/100) 2 , resulting in easily sufficient bandwidth to operate at 10 Mbps.

For many high-speed systems the skin effect is the most significant bandwidth-limiting factor. At extremes of frequency, however, the skin effect is superceded by dielectric loss. In the dielectric-loss-limited region the constant h asymptotically approaches a value of 1. In the dielectric-limited region the relation between speed and distance becomes merely inverse, not inverse-squared.

For dielectric-effect limited media, doubling the length while slowing down to 1/2 the bit rate produces the same eye pattern .

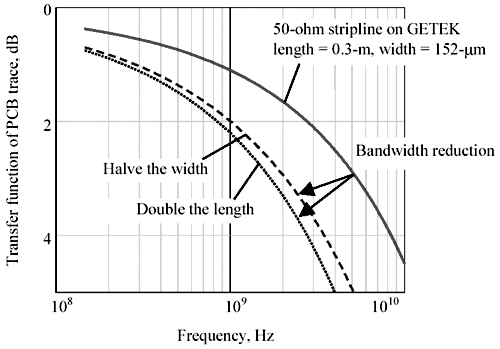
Fortunately for high-speed digital designers, the bandwidth of a typical pcb trace is pretty incredible. Figure 3.42 illustrates the performance of a 152- m m (6-mil) stripline trace implemented on Getek. The trace is 0.3-m long. The 3-dB attenuation point for this trace occurs at 5 GHz.

Figure 3.42. Either doubling the line length or halving the line width cuts bandwidth by a big factor.

If this sort of performance is not enough for your application, let me explain how to get even higher bandwidth. These ideas build on a simple approximation for transmission-line attenuation:

Equation 3.150

 

where	a is the attenuation in decibels,
	w is the frequency of operation, rad/s,
	l is the length of the transmission line in meters,
	w is the frequency at which AC line parameters are specified, rad/s,
	R is the AC resistance of the line at frequency w ,
	Z is the characteristic impedance of the line at frequency w ,
	v is the velocity of propagation at frequency w , m/s, and
	tan q is loss tangent of the dielectric material at frequency w .

This expression contains many terms; there should therefore exist many ways to reduce the attenuation, thus increasing the 3-dB bandwidth.

1. Use more copper. If you want higher bandwidth, try using wider traces (for cables, use bigger signal conductors). At the same time you make the trace wider, also raise it up further away from the nearest solid plane. This change results in a new geometry with the same impedance as the original, but less resistance R . The resistance R varies inversely with trace width.

   NOTE: Above 1 GHz the dielectric losses become rapidly more significant than skin-effect losses. Monkeying around with skin-effect loss in a system that is dominated by dielectric problems makes progressively less and less sense as you go to frequencies far above w q .

2. Don't go as far. In the skin-effect zone the bandwidth varies inversely with the square length; in the dielectric zone it's an inverse relationship. Either way, longer traces have less bandwidth. If you must go a long way, consider using repeaters.
3. Use a higher-impedance trace. Moving your signal conductor farther from its nearest return path (without increasing its trace width, or diameter) increases the Z while leaving R mostly unchanged. This adjustment lowers the ratio R / Z , lowering the skin-effect attenuation, thus raising the bandwidth. Unfortunately, this method has the side effect of rendering the trace more susceptible (percentage-wise) to lumped capacitive loads.
4. Do something so the attenuation doesn't matter. Fixed equalization can extend the operating distance by at least 50%. This approach is used in the popular 10BASE-T Ethernet standard at 10 Mb/s over category-3 unshielded twisted-pair wiring (see Section 8.2, "UTP Transmission Example: 10BASE-T"). Fixed equalization may be incorporated into the driver, the receiver, or a combination of both. Adaptive equalization is a more powerful technique, although more difficult to design. It can in some cases more than double the operating distance. An adaptive equalization approach is used in many 100BASE-X Ethernet chips at 100 Mb/s over category-5 unshielded twisted-pair wiring. In systems with very low levels of background noise, and where the complexity of the receiver is not an objection, multilevel coding can provide even greater benefits. The 1000 Mb/s Ethernet standard for category-5 unshielded twisted-pair wiring (1000BASE-T) combines adaptive digital equalization, multilevel coding, and adaptive digital cancellation of near-end crosstalk to obtain a signaling rate of 250 Mb/s per pair on 100-m lengths of category-5 unshielded twisted-pair cabling.
5. Use a better dielectric material. The lower the loss tangent of the material, the less dielectric loss your signals will endure. Less dielectric loss translates to higher bandwidth. A lower dielectric constant, even with the same loss tangent, also helps because that increases the propagation velocity v , lowering dielectric losses.

As technology advances, more options become available. You can look at recent LAN standards to get a glimpse of what may someday become commonplace in ordinary digital logic families. For example, fixed equalization (10BaseT), adaptive equalization (100BaseTX), and multilevel coding with digital adaptive filtering and near-end crosstalk cancellation (1000BaseT) are fast becoming mass-market realities.

Many designs have not yet reached the point at which trace bandwidth becomes a serious limitation, but just you wait. When typical trace widths go down to 0.002 in. and typical clocks reach 1 GHz, you'll be there.

POINT TO REMEMBER

• Five ways to improve the performance of a copper transmission channel: use more copper, don't go as far, use a higher characteristic impedance, add equalization, or use a better dielectric material.