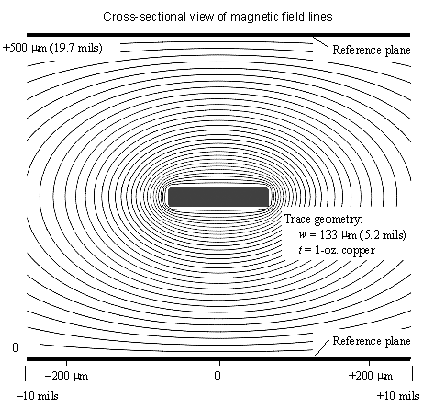
Pcb Signal Propagation

5.1.1 Characteristic Impedance and Delay

At this point in time, all major pcb CAD packages incorporate 2-D field solvers. These tools are extremely effective at calculating transmission-line impedance and delay, so much so that a listing of the old transmission-line impedance approximations would be of little use to the average reader. The values computed for impedance and delay correspond to the variables Z and v in the signal propagation model of Chapter 3.

If you don't already have a 2-D field solver, get one. If you absolutely cannot afford an automated tool, at least get a copy of Wadell [41] . His book lists all the closed-form approximation formulas for impedance and propagation delay of transmission-line configurations that were known as of the time of publication, including microstrips, striplines, some coplanar structures, and various differential arrangements. Failing that, this author modestly recommends the formula sets included in the appendices of [51] .

In a practical sense, what you need to know about pcb-trace impedance is that it varies approximately with the square root of trace height, inversely with the square root of width, and inversely with the square root of the effective dielectric constant. These variations are not exact, but indicate generally the sensitivity of trace impedance to the parameters of width and height. The trace thickness is a secondary parameter.

For striplines, the effective dielectric constant (and thus the delay) is entirely determined by the dielectric constant of the surrounding substrate material. For microstrips, the effective dielectric is somewhat less (see 5.1.3.1, "Estimating the Effective Dielectric Constant for a Microstrip"). Examples are given in Table 5.1.

Because parameters for skin-effect resistance and dielectric loss are less broadly disseminated, I shall endeavor to provide some guidance on those matters.

POINT TO REMEMBER

• If you don't already have a 2-D field solver, get one.

 

5.1.2 Resistive Effects

5.1.2.1 DC Resistance of Pcb Trace

The formula for the nominal DC resistance of a rectangular pcb trace is given in [2.41] (Section 2.4, "DC Resistance").

POINT TO REMEMBER

• A 1/2-oz copper pcb trace with 100- m m (3.9 mil) width has a DC resistance of 9.6 W /m. The DC resistance scales inversely with the width and inversely with the copper plating weight.

 

5.1.2.2 AC Resistance of Pcb Trace

The proximity effect for pcb traces takes hold at rather low frequencies on the order of a few megahertz . Below that frequency the magnetic forces due to changing currents in the traces are too small to influence the patterns of current flow. Low-frequency current in a pcb trace therefore follows the path of least resistance , filling the cross-sectional area of the trace, flowing uniformly throughout the signal conductor. That same current, as it returns to its source through the power-and-ground planes, tends to spread out in a wide, flat sheet, occupying as much of the surface area of the planes as possible on its way back to the source. That is the least resistive path through the planes.

Above w LC (a few Megahertz for most pcb traces) the magnetic forces surrounding a trace become quite significant, so much so that they change the patterns of current flow. The current is forced into a new distribution dependent not on the trace resistance, but on the trace inductance. This new distribution follows the path of least inductance , which is by definition that distribution of current that minimizes the total stored magnetic field energy surrounding the trace. Since the path of least inductance differs by definition from the path of least resistance, you would expect effective trace resistance to be increased when current is forced to flow in this high-frequency mode.

The magnetic fields constrain the high-frequency current in two ways. First, the current is confined to a shallow band of depth d around the perimeter of a conductor, increasing the apparent resistance of the trace. This increase in apparent resistance is called the skin effect.

Next , the magnetic fields distribute the current around the perimeter of the conductor in a non-uniform manner (the proximity effect). The relative increase in the apparent resistance of the conductor due to this non- uniformity , above and beyond what you would expect from the action of the skin effect alone, is represented by the proximity factor k p .

The proximity effect draws signal current towards the side of a microstrip facing the reference plane, or that side of a stripline that faces the nearest reference plane. It simultaneously concentrates the returning signal current on the reference plane, forming it into a narrow band that flows on the plane, staying mostly underneath the signal trace.

The increase in resistance of a typical high-speed digital signal conductor due to the proximity effect (above and beyond simple consideration of the skin depth and trace circumference assuming a uniform current distribution) typically ranges from 25% to 50%. This fraction remains fixed at all frequencies high enough for the effect to have taken hold (typically somewhere in the vicinity of w LC ).

Another similar- sized increase in resistive dissipation occurs due to the nonuniform distribution of current on the reference plane. At DC, you can assume that current spreads widely in all directions, so the DC reference-plane resistance should be (nearly) zero. At high frequencies, however, the returning signal current in the planes flows most heavily just underneath your trace, with wide tails of residual current falling off (at least) quadratically as you move away from the trace on either side. The current in this reference-plane distribution, because it remains well concentrated in a narrow band underneath the signal conductor, dissipates a noticeable amount of power, typically on the order of 25% to 50% of the signal-trace dissipation. This fraction remains fixed at all frequencies high enough for the effect to have taken hold.

The proximity factor takes into account the additional resistance due to redistribution of current on both the signal conductor and the reference planes.

Table 5.1 lists values of the AC resistance R and proximity factor k p for typical trace geometries used in high-speed digital designs. The value of R already incorporates k p ; I'm just showing the k p in case you want to use it to work out other similar configurations later and so you can see how gradually it changes with trace geometry.

In Table 5.1, parameter w is the trace width, h the height of the bottom surface of the trace above the lower reference plane, and b (striplines only) the separation between the planes (Figure 5.2). The microstrips listed in Table 5.1 assume 1-oz copper (including plating) with a conformal coating (soldermask) consisting of a 12.7- m m (0.5-mil) layer having a dielectric constant of 3.3. The stripline examples assume 1/2-oz bare copper. The resistance data was developed using a method-of-moments magnetic field simulator with 120 segments equally spaced around each pcb trace, with the current linearly interpolated across each segment, and three points at each corner rounded to fit a circular arc. The author estimates the accuracy of the data generated by this simulator at approximately +/ 2%.

Figure 5.2. Printed-circuit trace configurations are defined by parameters w , t , h , and b .

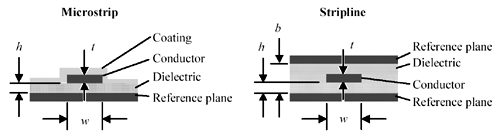
Table 5.1 assumes a dielectric constant of 4.3. If you are working with a different dielectric constant, you should know that what matters most for determining the proximity factor is the ratio w / h . The ratio t / h , assuming the trace is thin compared to its width, is of secondary importance. Traces with similar ratios of w / h inherit similar values of k p regardless of the dielectric constant.

Table 5.1 does not take into account either surface roughness or the inevitable random variations in trace width that occur in real boards .

Table 5.1. AC Resistance and Skin Effect Loss at 1 GHz for Selected Single-Ended Microstrips and Striplines

h mil	w mil	b mil	R AC W /in.	R AC W /m	k p	a r dB/in.	a r dB/m	Z W	re
50-ohm microstrips, 1-oz copper with soldermask
10	17.9	n/a	0.420	16.5	1.953	.036	1.44	50	3.24
9	16.0	n/a	0.460	18.1	1.928	.040	1.57	50	3.24
8	14.0	n/a	0.513	20.2	1.903	.045	1.75	50	3.24
7	12.1	n/a	0.578	22.7	1.878	.050	1.98	50	3.24
6	10.2	n/a	0.663	26.1	1.851	.058	2.27	50	3.25
5	8.3	n/a	0.780	30.7	1.820	.068	2.67	50	3.25
60-ohm microstrips, 1-oz copper with soldermask
10	12.5	n/a	0.531	20.9	1.776	.038	1.51	60	3.16
9	11.1	n/a	0.583	23.0	1.754	.042	1.66	60	3.16
8	9.7	n/a	0.648	25.5	1.731	.047	1.85	60	3.16
7	8.3	n/a	0.730	28.8	1.704	.053	2.08	60	3.16
6	6.9	n/a	0.839	33.0	1.675	.061	2.39	60	3.16
5	5.6	n/a	0.981	38.6	1.650	.071	2.80	60	3.16
70-ohm microstrips, 1-oz copper with soldermask
10	8.8	n/a	0.665	26.2	1.631	.041	1.62	70	3.10
9	7.8	n/a	0.728	28.7	1.609	.045	1.78	70	3.10
8	6.7	n/a	0.813	32.0	1.584	.050	1.99	70	3.10
7	5.8	n/a	0.905	35.6	1.566	.056	2.21	70	3.10
6	4.8	n/a	1.036	40.8	1.542	.064	2.53	70	3.10
5	3.8	n/a	1.215	47.8	1.516	.075	2.97	70	3.10
50-ohm striplines, 1/2-oz bare copper
5	3.5	10	1.498	59.0	1.513	.013	5.12	50	4.30
5	5.1	15	1.144	45.0	1.597	.099	3.91	50	4.30
7	5.8	15	1.014	39.9	1.586	.088	3.47	50	4.30
5	5.7	20	1.074	42.3	1.655	.093	3.67	50	4.30
7	7.2	20	0.865	34.0	1.646	.075	2.96	50	4.30
10	8.0	20	0.782	30.8	1.637	.068	2.67	50	4.30
5	6.2	30	1.033	40.7	1.714	.090	3.53	50	4.30
7	8.5	30	0.782	30.8	1.732	.068	2.67	50	4.30
10	11.1	30	0.609	24.0	1.729	.053	2.08	50	4.30
15	12.7	30	0.533	21.0	1.722	.046	1.82	50	4.30
NOTESAC parameters R AC , a r , Z , re , and FR-4 dielectric r = 4.30 are all specified at 1 GHz. The microstrip examples assume copper traces of 1-oz thickness (including plating) with s = 5.9810 7 S/m plus a conformal coating (soldermask) consisting of a 12.7 m m (0.5-mil) layer having a dielectric constant of 3.3. The stripline examples assume copper traces of 1/2-oz thickness with no plating.

The other columns listed in Table 5.1 are

• a r resistive trace loss (dB/m 1 GHz)
• Z real part of characteristic impedance ( W at 1 GHz)
• re dielectric constant (real part of effective relative electric permittivity) at 1 GHz

The propagation velocity v (m/s) and delay t p (s/m) are found from re , where 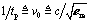and c = 2.99810 8 m/s. The DC resistance constant k a is unity for all the single-ended pcb trace examples in Table 5.1.

Modern 2-D electromagnetic field solvers automatically calculate the proximity effect when reporting skin-effect resistance.

POINTS TO REMEMBER

• Low-frequency current in a pcb trace therefore follows the path of least resistance , filling the cross-sectional area of the trace.
• The skin effect confines high-frequency current to a shallow band of depth d around the perimeter of a conductor.
• The proximity effect draws signal current towards the side of a microstrip facing the reference plane, or that side of a stripline that faces the nearest reference plane.
• The increase in resistance of a typical high-speed digital signal conductor due to the proximity effect (above and beyond simple consideration of the skin depth and trace circumference assuming a uniform current distribution) typically ranges from 25% to 50%.
• Another similar-sized increase in resistive dissipation occurs due to the nonuniform distribution of current on the reference plane.
• Traces with similar ratios of w / h inherit similar values of k p regardless of the dielectric constant.

 

5.1.2.3 Calculation of Perimeter of Pcb Trace

When using [2.43], [2.44], or [2.63] to estimate the total series resistance R AC of the conductor, taking into account both skin effect and proximity effect, the perimeter of the signal conductor is defined

Equation 5.1

 

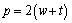
where	p is the perimeter of the conductor (m), and
	w and t are the width and thickness of the signal conductor respectively (m).

5.1.2.4 Very Low Impedance Pcb Trace

In the limit as the trace height h approaches zero (and the impedance descends towards zero), the trace concentrates all its current on the reference-plane facing side of the trace, with none on the reverse side. This doubling of the current density on one side doubles the apparent resistance. In addition, the trace suffers from an identical distribution of current on the reference plane, doubling the result again, for a total of k p 4.0.

5.1.2.5 Calculation of Skin-Effect Loss Coefficient for Pcb Trace

The skin-effect loss in units of nepers per meter is given by [3.114]:

Equation 5.2

 

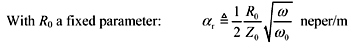
where	R is the skin-effect resistance ( W /m) at the particular frequency w .
NOTE:	This formula applies only at frequencies above the onset of the skin effect.

If the line resistance R ( w ) is specified as a function of frequency, the resistive loss coefficient in units of nepers per meter equals,

Equation 5.3

 

For microstrips, Pucel et al. [45] (and [52] , which is reproduced in [41] ) provide empirical closed-form approximations for the calculation of a r . A spot-check comparison of values from Pucel's closed-form expressions with the values listed for resistive loss in Table 5.1 reveals a corroboration error of about 2%.

5.1.2.6 Popsicle-Stick Analysis

Article first published in EDN Magazine , March 7, 2002

You can simulate the magnetic field surrounding a pc-board stripline using a rubber sheet and a Popsicle stick. First, stretch the rubber sheet over a rectangular frame. Then square off the end of the Popsicle stick and push it into the rubber (Figure 5.3). Your simulation shows the magnetic-field potential surrounding the pc-board trace.

Figure 5.3. A rubber sheet simulates the magnetic field structure surrounding a stripline.

A close look at the precise forces bearing on the end of the stick teaches you a lot about stripline behavior. First, note that the force required to support the rubber sheet is not uniform at all points at the end of the stick. Because the stick is flat across its end face and because the rubber sheet is assumably lightweight, the forces acting on the stick are practically zero everywhere except around the edges of its end face. As a result, you don't really need any meat in the center of the stick; a hollow stick would do just as well.

Next, check the distribution of force around the edges of the end face. It's not uniform either. With a round, hollow stick, you might expect a uniform distribution of force where the edges of the stick meet the rubber, but when a rectangular stick presses against the rubber, the corners bear a disproportionate share of the weight. You know this if you have ever erected a big tarp for a picnic shelter. Once you put the corner posts in place and stretch the tarp so it is taut, your work is nearly complete. The corners do most of the work of holding up the tarp, and all you must do to complete the job is provide minor supports every so often to keep the sides and middle from sagging (or leave them to sag). In Figure 5.3, the wire frame lines near the tip of the protrusion show the same effectthe sheet is stretched hardest at the corners.

The greatest concentrations of current prevail on the inside-facing surfaces of opposing conductors.

 

Now to the point of this article, which is the correspondence between the rubber-sheet world and the electrical world. The flat end of the stick represents the cross section of a pc trace, the rectangular frame represents reference planes above and below the trace, and the protrusion of the rubber sheet mimics the magnetic potential. The slope of the rubber sheet at any point indicates the magnetic-field intensity. Contour rings drawn on the rubber sheet at constant heights above the frame show familiar "magnetic lines of force" typically used to depict magnetic fields (Figure 5.4).

Figure 5.4. The magnetic field is most intense near the ends, and especially the corners, of a stripline trace.

A direct correspondence exists between the forces acting on the end of the Popsicle stick, which induce curvature in the rubber sheet, and the density of electrical currents flowing in a pc-trace of a similar cross-section profile. These currents likewise induce curvature in the magnetic potential. Where the rubber sheet is flat (no curvature), there is no force, and in the electrical world, there is no current. Where the rubber sheet is most tightly curved (at the corners), the force acting on the stick and also the density of current are greatest.

From this simple analogy you may conclude that high-frequency current flows only around the periphery of a trace, not in the middle. Such is the case at frequencies that are sufficiently high that the skin depth shrinks to much less than the conductor thickness, a condition required for the analogy to hold. Some other conclusions that flow easily from Popsicle-stick analysis include the following:

1. The density of current near the corners of a trace profile, such as the forces acting near the corners of a Popsicle stick, exceeds the density of current elsewhere. Because traces tend to be thin and wide, a concentration at the corners has the same general effect as a concentration on either side of the trace. This effect is called edge-current concentration , the mathematics of which are predicted by rubber-sheet analysis.
2. If you make a differential pair by placing a signal conductor and a return conductor in close proximity, with the signal stick pressing up on the rubber sheet while the return conductor presses down (Figure 5.5), the greatest concentrations of current will prevail on the inside-facing surfaces of the two conductors where the magnetic potential traverses from peak to valley in the least distance (Figure 5.6). The concentration of current at the inside-facing edges is called the proximity effect .

   Figure 5.5. The magnetic potential surrounding a differential stripline is elevated at one conductor and depressed at the other.

   

   Figure 5.6. (Detail from Fig. 5.5)A steeper slope prevails on the side facing the other conductor.

   

3. If a stripline trace is offset towards one reference plane, the slope of the rubber sheet on that side (and thus the force) must necessarily increase, indicating a larger concentration of current on the side of the trace facing the reference conductor than on the opposing side. This effect increases the apparent resistance of a signal trace above the value predicted, assuming a uniform distribution of current around the periphery of the conductor.

I know people who have spent years studying the mathematics behind these three conclusions but still don't understand why they happen. You've just grasped the whole subject in a few minutes, and you got to enjoy a Popsicle!

POINT TO REMEMBER

• You can simulate the magnetic field surrounding a pc-board stripline using a rubber sheet and a Popsicle stick.

 

5.1.2.7 Nickel-Plated Traces

High Speed Digital Design Online Newsletter , Vol 5, Issue 6

Paul Greene writes

I am an engineer with Rexcan Circuits, a pcb manufacturer in Ontario. We are evaluating various processes for the use of immersion gold. We are depositing approximately .00012 in. nickel followed by .000005 in. gold over the copper pads. I am investigating the effect of two alternate procedures:

1. Coating all the traces/pads with nickel and then applying soldermask, versus
2. Applying soldermask over the traces first and then coating only the pads with nickel and gold.

We have been advised that due to the changes to the skin effect caused by the Ni/Au on the traces, we could be building in a problem for high-frequency RF designs. Can you find time to comment? I have run some characteristic impedance tests at around 65 Ohms using a TDR tester and not seen much difference. Is nickel a real problem?

I hope you don't mind my contacting you, but your Web page has lots of good stuff in this area!

Reply

Thanks for your interest in High-Speed Digital Design . I've received a number of letters since writing " Steel -Plated Power Planes," pointing out that nickel is magnetic too, and a well-established chemistry exists for plating it onto copper. That's an interesting point. Of course the magnetic permeability of nickel is nowhere near that of steel, so you won't get nearly as dramatic an effect, but it might be worth investigating.

Regarding your specific question, I've often wondered about the same issue. I presume you are familiar with the concept of the skin effect and how current at high frequencies flows only on the outer surface (skin) of your conductor, not in the middle. Because of the high magnetic permeability of nickel, the skin-effect resistance on the nickel-plated side of your conductor will be considerably higher than that on the bare-copper side ( core side).

You might be tempted to think that this will be okay because even if one side of the trace is messed up because of the nickel plating, you've still got a good copper surface on the bottom of the trace. The bottom-side surface acts in parallel with the nickel-plated side, so even if the nickel-plated resistance were infinite, the overall resistance of the configuration you might think would be no more than twice as bad as an all-copper trace. Unfortunately, that is a very poor analogy. At high frequencies the current distributes itself around the periphery of your trace in a pattern that minimizes the total inductance of the trace configuration without regard to the skin resistance of the trace . That is, if you change the skin-effect resistance on one side (by plating), then in the limit at very high frequencies you hardly change the distribution of current around the periphery of trace at all.

That action is contrary to the way current behaves at DC. At DC, current distributes itself to minimize the total dissipated power. For example, imagine two resistors R t and R b in parallel, both with resistance 2 W . The overall (parallel) resistance is 1 W . If you double the value of R t (changing its value to 4 W ), the DC resistance of the parallel combination becomes (4 W 2 W )/(4 W +2 W ) = (4/3) W . Driven with a constant DC current, you get less current in R t , but more in R b , in a combination that minimizes the total dissipation. No matter how high you make the value of R t , the resistance of the parallel combination never gets bigger than 2 W .

At high frequencies, the same effect does not prevail. At high frequencies, the current distributes itself in a way that minimizes the overall inductance (this minimizes the energy stored in the magnetic field surrounding the circuit). In a pcb trace, this means the ratio of currents on the top and bottom of the trace are fixed by the inductance and will not respond to modest changes in the surface resistivity of the two surfaces.

Going back to the example of resistances R t and R b , suppose R t represents the resistance of the top surface of your microstrip trace and R b the bottom surface, both with resistance equal to 2 W . In response to a DC current of 1A, each resistor initially dissipates 0.5 W, for a total dissipation of 1 W. If you double the resistance of the top surface without changing the distribution of current, the power dissipated in R t doubles while the power in R b remains at 0.5 W. The total dissipation jumps to 1.5 W. You could look at this and say that the effective resistance of the combination went up by 50% (to 1.5 times the original value).

If you multiply the resistivity of the top surface in the present example by 10, the effective resistance goes up to (0.5) 10 + (0.5) = 5.5. Continued increases in surface resistivity of the top side make almost unlimited increases in the overall effective resistance.

Let's calculate how bad the effect can get for a nickel-plated microstrip.

• The resistivity of nickel exceeds that of copper by a factor of k = 4.5.
• The relative magnetic permeability of nickel at 1 GHz is in the range of 5 to 20 (take u r = 10 as a nominal value).
• The increase in surface resistance of nickel at 1 GHz (above and beyond that of copper at 1 GHz) equals the square root of k u r , which works out to about 6.7.
• The current density on the top side of a 50-ohm FR-4 pure-copper microstrip contributes about 1/3 the total dissipation. If you increase that 1/3 of the dissipation by a factor of 6.7, then I would expect an overall increase in resistive trace loss by a factor of (1/3) 6.7 + (2/3) = 2.9, roughly tripling the resistive trace loss.
• The effective length at which you may use a high-speed pcb trace varies almost inversely with resistive trace loss.

At frequencies on the order of 1 GHz, the nickel-plating cuts in third the effective useful length of your traces .

I checked the skin depth of nickel at 1 GHz (see equation [2.42]) and found it's about 1.4 m m (0.055 mil), much thinner than your nickel plating. If you could make the nickel plating as thin as the gold, it won't raise the trace resistance, but I bet it doesn't work as a barrier layer if it's that thin.

In a TDR waveform, any series resistance present in a conductor causes an upward tilt to observed waveform. You can think of this as the trace showing slightly less impedance at first (high frequencies), then gradually transitioning to a larger value of impedance as time goes by (lower frequencies). The amount of tilt is related to the amount of series resistance. I predict your nickel-plated traces will show a greater upward tilt than your bare-copper traces. That is one way you can determine the extent of the effect (ultimately, this test measures the magnetic permeability, and thus the purity, of your nickel).

If you look carefully at the TDR step edge that returns from the far end of a long (perhaps 10-in.) line, you should see a noticeable degradation in the risetime. This degradation will be worse on the nickel-plated traces than on the bare copper traces.

The effect of nickel plating is real and commonly understood in the microwave community.

POINT TO REMEMBER

• At frequencies on the order of 1 GHz, nickel-plating the top surface of a microstrip cuts in third the effective useful length of the trace.

 

5.1.3 Dielectric Effects

Microwave designers worry a lot about dielectric loss. The dielectric-loss problem is particularly acute when constructing high-Q circuits intended to ring without signal amplitude loss for many cycles. As a result, microwave designers often choose ceramic substrates, like alumina, that have excellent dielectric loss properties in the gigahertz regime . Digital designers typically avoid high-Q circuit topologies and so are not nearly as sensitive to dielectric loss.

For FR-4 digital circuit board applications at operating frequencies below 1 GHz (corresponding to the highest frequency of interest in the rising and falling edge spectra of a system with rise and fall times of 500 ps), at distances up to 10 inches, you may safely ignore dielectric losses. At longer distances or at higher speeds, dielectric losses can become quite significant.

POINTS TO REMEMBER

• For FR-4 digital circuit board applications with risetimes of 500 ps or slower, at distances up to 10 inches, you may ignore dielectric losses.
• At longer distances or at higher speeds, dielectric losses can become quite significant.

 

5.1.3.1 Estimating the Effective Dielectric Constant for a Microstrip

A stripline trace contains all (or most of) its electric fields within the dielectric cavity formed between two solid conducting reference planes. The dielectric properties of stripline traces therefore depend only on the dielectric constant and loss tangent of the pcb material.

Microstrips, on the other hand, contain only part of their electric field within the dielectric layer. The remainder spews up into the air. The microstrip configuration therefore constitutes a type of mixture dielectric with properties intermediate between the properties of the dielectric substrate and air. The effective permittivity for a microstrip depends on the geometry of the trace and the proportion of total field energy stored in each of the two regions .

Many empirical closed-form approximations exist for the calculation of effective permittivity. The book by Gupta [39] provides numerous references for such approximations. The particular form of Gupta's equations reported here comes from a paper by I. J. Bahl and R. Garg [50] .

Equation 5.4

 

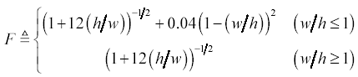
Equation 5.5

 

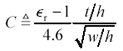
Equation 5.6

 

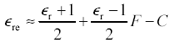
where	w , h , and t are the width, height, and thickness respectively of a pcb microstrip (m),
	r represents the real part of the relative electric permittivity (dielectric constant) of the substrate material,
	re represents the real part of the effective relative electric permittivity (also called effective dielectric constant) of the complete transmission configuration,
	C and F are empirically derived constants, and
	no limits to accuracy or applicability were supplied with this equation.

A spot-check comparison of values from Bahl and Garg's closed-form expression with the values for effective dielectric constant listed in Table 5.1 reveals a corroboration error of about 3%.

For striplines, re = r .

POINT TO REMEMBER

• A microstrip has dielectric properties intermediate between the properties of the dielectric substrate and air.

 

5.1.3.2 Propagation Velocity

From the effective dielectric constant re , you may determine the propagation velocity.

Equation 5.7

 

where	c is the velocity of light in vacuum , 2.99810 8 m/s,
	re is the effective relative electric permittivity (also called effective dielectric constant) of the complete transmission configuration, and
	v is the velocity of propagation (m/s).

Examples showing the variation in re (and thus trace delay) for various microstrip trace geometries appear in Sections 5.1.3.6, "Passivation and Soldermask," 12.4, "Stripline vs. Microstrip Delay," and 6.10.1, "Differential (Microstrip) Trace Impedance." The effective relative permittivity for a stripline always equals the relative permittivity of the substrate material.

5.1.3.3 Calculating the Effective Loss Tangent for a Microstrip

For striplines, the loss tangent of the transmission configuration equals the loss tangent of the substrate material.

For microstrips, you may determine the effective loss tangent of the transmission configuration given three pieces of information:

tan q	The loss tangent of the substrate material,
r	The real part of the relative electric permittivity (also called dielectric constant) of the substrate material, and
re	The real part of the effective relative electric permittivity (also called effective dielectric constant) of the complete transmission configuration.

Assume you know tan q and r , but not re . Here are several ways to glean re .

• From knowledge of the effective propagation velocity, presumably given by a 2-D electromagnetic field solver, you may invert equation [5.7],
• From the direct output of a 2-D electromagnetic field solver,
• By interpolation from the values of re listed in Table 5.1, or
• By the closed-form approximation [5.6].

Once all three parameters are known, the effective loss tangent of the microstrip configuration is determined (see [2.87]):

Equation 5.8

 

where	r is the real part of the relative electric permittivity (also called dielectric constant) of the substrate material,
	re is the real part of the effective relative electric permittivity (also called effective dielectric constant) of the transmission configuration,
	tan q is the loss tangent of the substrate material, and
	tan q e is the effective loss tangent of the transmission configuration.

Microstrips do have a small advantage over striplines in regards to the loss tangent, which, due to the partial propagation in air, is somewhat less than what would be experienced by a stripline. For example, using values from Table 5.1, tan q e for a 50-ohm microstrip implemented in FR-4 ( k = 4.3) is approximately 90% of the native tan q of the underlying substrate.

5.1.3.4 Dielectric Properties of Laminate Materials (Core and Prepreg)

Core and prepreg laminate materials are now available in a staggering array of types and variations. A core laminate is a piece of insulating material with copper sheet bonded to both sides, ready for etching. A prepreg laminate is a sheet of insulating material, often in a partly cured state, that is inserted between etched cores to build up a finished multilayer pcb. The prepreg sheet, once heated and pressed in the stacking operation, cures into a material very similar to the insulation used in the cores.

Table 5.2 lists generic properties of selected materials used in pcb construction. Please remember that these are gross ballpark numbers for materials in pure form. All manufacturers add fillers to their resin mixture to improve properties such as toughness, foil adhesion, pot life, and so forth. The filler materials modify the dielectric and mechanical properties. The purpose of the table is to indicate in a general way the magnitude of the improvement to be had from switching between various materials.

In most high-speed digital products, the core or prepreg laminate comprises a fabric of fine threads embedded in a solidified resin. The threads may be made of glass, quartz, Kevlar (a trademark of DuPont), or some other durable material. Names associated with those materials are e-glass, s-glass, quartz, and aramid (Kevlar) fibers. The fabric imparts a great deal of mechanical stability to the finished core but creates a fundamentally inhomogeneous material with an uneven surface.

Table 5.2. Properties of Selected Materials in Pure Form

Material	r 1 MHz	tan q 1 MHz	Specific gravity g/cm 3	Source
Natural materials
Hard vacuum	1.0000
Air	1.0005		0.0012	at STP, CRC Handbook
Water	80		0.998	at 20 C, CRC Handbook
Pcb resins
Epoxy (as used in FR-4)	3.8	0.049	1.54	r is extrapolated from Harper [36] , p. 8.46; tan q and specific gravity inferred from Park/Nelco specification of N4000-2 laminate
Cyanate ester	3.	0.023	1.29	r is extrapolated from Harper [36] , p. 8.45; tan q and specific gravity inferred from Park/Nelco specification of N8000 laminate at 1 GHz; values as low as 0.005 have been reported for tan q by IBM [37]
Polyimide	3.3	0.029	1.33	r comes from www.zeusinc.com , a manufacturer of polyimide resin; tan q inferred from Park/Nelco specification of N7000 laminate at 1 GHz; specific gravity from www.maropolymer.com
PTFE	2.1	< .0002	2.14 to 2.20	www.mdmetric.com , a manufacturer of PTFE resin
Pcb fibers
e-glass	5.8	.0011	2.54	Harper [36] , p. 8.26
s-glass	4.52	.0026	2.49	Harper [36] , p. 8.26
Quartz	3.5	.0002	2.20	Harper [36] , p. 8.26
Aramid (Kevlar)	4.0	.001	1.40	Harper [36] , p. 8.26
Other substrates
Alumina				T. C. Edwards [38]
99.5%	10.1	0.0001 to 0.0002
96%	9.6	0.0006
85%	8.5	0.0015
Si (high resistivity)	11.9	0.001 to 0.01		T. C. Edwards [38]
GaAs	12.85	0.0006		T. C. Edwards [38]
Single-crystal sapphire	9.4, 11.6 [1]	0.00004 to 0.00007		T. C. Edwards [38]
Fused quartz	3.8	0.0001		T. C. Edwards [38]

[1] NOTE (1)Sapphire is an anisotropic medium and so has different dielectric constants in different directions.

The resin fills the spaces between fibers, forming a sturdy matrix with a smooth surface for supporting traces, vias, and other pcb structures. Popular resin systems include various epoxies, cyanate ester, polyimides, and polytetrafluoroethylene (PTFE, also known by the trade name Teflon).

Fiber materials are selected on the basis of strength, coefficient of thermal expansion, dielectric constant and loss, hardness (which affects the lifetime of your drill bit), and cost.

Resin systems are selected on the basis of strength, glass transition temperature T g , dielectric constant and loss, and cost. T g is the temperature near which a resin begins to soften and become gooey, and its mechanical properties undergo substantial change. For example, above T g most pcb resins undergo substantial z-axis expansion. A human wouldn't particularly notice the expansion, but since it exceeds the thermal expansion of copper, it can easily rip apart pcb vias. The pcb resin materials in Table 5.2 are listed in order of increasing T g , ranging from ordinary FR-4 epoxies in the range of 125 C to 150 C to BT/epoxy (not listed) at 185 C, cyanate ester at 245 C, and polyimide at 285 C [42] [44] . The PTFE material doesn't have a glass transition temperature, it just melts, but only at very high temperatures (so high that it makes a great cooking surface).

There are other categories of laminates, including ceramic structures used in multichip modules and some space applications. Ceramics are mechanically stable and can have an exceptionally low dielectric-loss tangent combined with a high dielectric constant. These properties make ceramics ideal for flip-chip mounting of microwave circuits. Microwave engineers like the high dielectric constant of alumina ( r 10) because it shrinks the size of the printed structures they use to produce