Appendix D. Accuracy of Pi Model

The transfer function H for a transmission line may be expressed in terms of the Taylor-series approximation for the exponential function.

Equation D.1

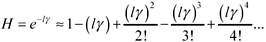
where	g is the propagation coefficient for the transmission line (complex nepers/m), and
	l is the length of the line (m).

The inverse of this function is similarly defined for negative exponents:

Equation D.2

 

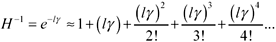
Taking only the first four terms of each expression, you can derive approximate formulas for the forms of H used in the calculation of system gain (Appendix C).

Equation D.3

 

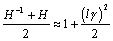
Equation D.4

 

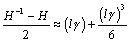
Now substitute approximations [D.3] and [D.4] into the expression for the gain of a fully configured transmission system [C.17].

Equation D.5

 

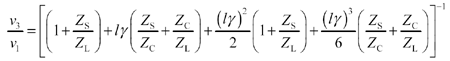
The next calculations compare [D.5] with the expression for the gain of a pi-model circuit in Section 3.4.2, Figure 3.4. The two-port transmission matrix for the pi-model circuit, fully configured with source and load impedances Z S and Z L respectively, is a composite of five two-port mini-models. The first (leftmost) matrix represents the series-connected source impedance. The next three represent the components in the pi-model. The last matrix represents the shunt-connected load impedance.

Equation D.6

 

The expression for the circuit gain follows :

Equation D.7

 

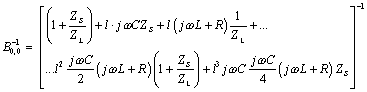
Next use the definitions of 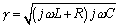and to derive the following substitutions:

Equation D.8

 

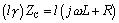
Equation D.9

 

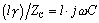
Plugging these new substitutions back into [D.7] leads to the following expression for the gain of the pi-model circuit.

Equation D.10

 

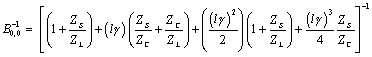
Comparing [D.10] with [D.5] reveals a perfect match of all zero-, first-, and second-order terms, with the lowest -order difference showing up in the third-order part of the expression. Assuming a small value of the propagation coefficient l g < 1/4, and thereby an overall gain somewhere near unity, you might reasonably conclude that the modeling error should not exceed the difference between [D.5] and [D.10]

Equation D.11

 

Further assuming the ratios Z S /(2 Z C ) and Z C / Z L to each be less than 3.8, the resulting pi-model error (measured as a function of frequency) should remain less than 1%.

As the coefficient l g grows, so grows the error in proportion to (at least) the third power of l g . At a value of l g < 1/2, you should expect a modeling accuracy no better than 1 part in 10.