Driving Multiple Loads with Source Termination

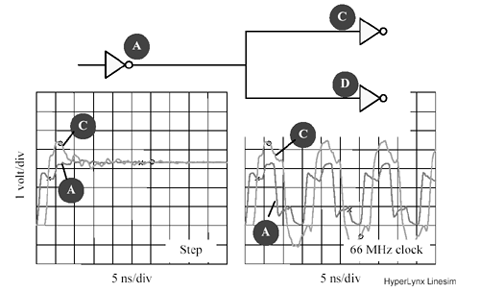
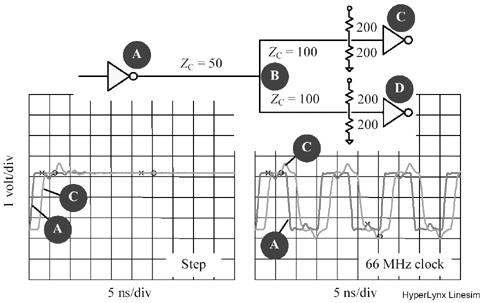
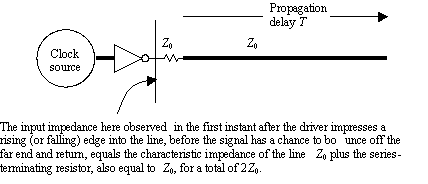
Figure 12.33 shows that in the first instant after the driver impresses a rising (or falling) edge into a source- terminated configuration, before the signal has a chance to bounce off the far end and return, the input impedance equals twice the characteristic impedance of the line. Not only that, the drive current requirement drops to zero after 2 T seconds, lowering the average power drain. These facts may tempt you to assume that a single gate designed to drive a single end-terminated configuration should be able to drive multiple (at least) source-terminated lines. That assumption is incorrect.

A careful examination of initial conditions, however, reveals that the peak drive current i PEAK for the source- and end-terminated lines are the same. For example, in Figure 12.33 the i PEAK required to initiate a full- sized rising edge into an impedance of 2 Z is V CC /2 Z .

Figure 12.33. The drive current required to initiate a full-sized rising edge at the end of the line is therefore V CC /2 Z .

An end-terminated example, assuming the end terminator is symmetrically split , may be analyzed using the Thevenin equivalent circuit of Figure 12.23. In the Thevenin equivalent circuit, because the battery is biased at the midpoint , the driver need only provide enough current to change the voltage at the input to R T by half of V CC in either direction. The i PEAK required is thus (1/2;)V CC / Z , precisely the same peak current required by the series terminator.

If your driver cannot pump out the required amount of current, then your initial rising edge at the receiver won't be full sized. Note that in the series-terminated case the driver does not have to meet V OH at the stipulated peak current, but you must know with some degree of precision what voltage your driver is guaranteed to produce when sourcing i PEAK . Given the voltage produced at the required i PEAK , the external series-terminating resistor is then sized to produce a voltage drop precisely equal to the difference between the driver output voltage at current i PEAK and the initial required voltage on the line, which is half of V CC . If the resistor is sized properly, the voltage-doubling effect at the unterminated far end of the line will ultimately bring the initial rising edge of the received signal up to exactly full value.

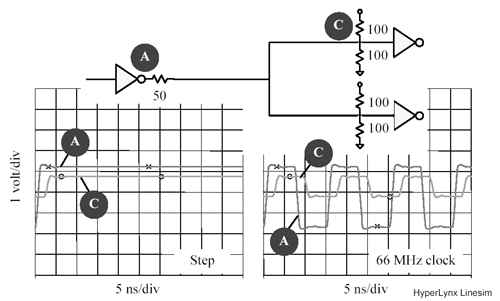
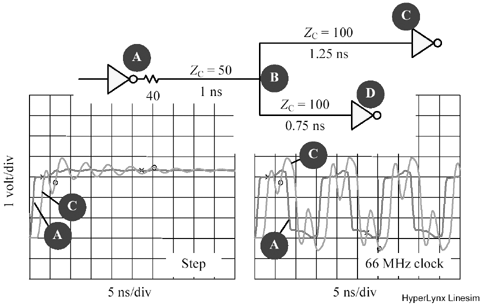
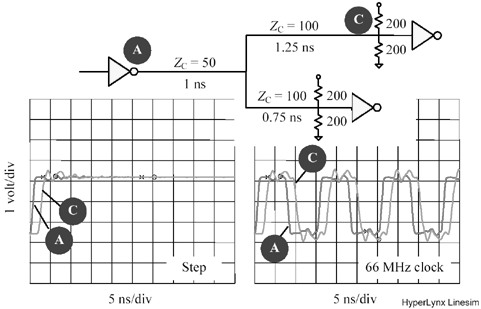
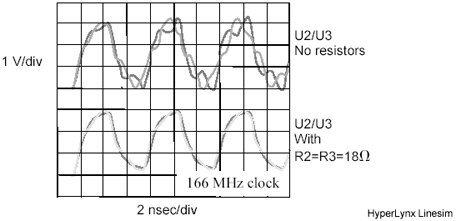
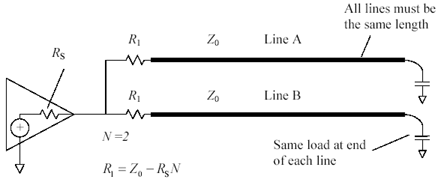
Some driver circuits can easily source enough current to drive two source-terminated lines. Is it possible to drive two or more source-terminated lines from such a driver? Yes, but only under the limited conditions diagramed in Figure 12.34.

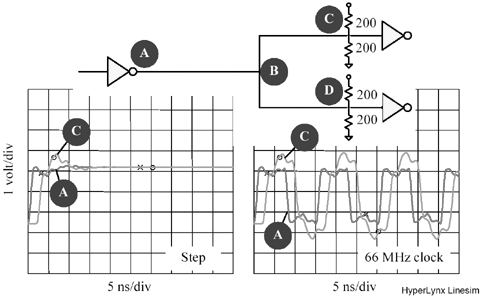
Figure 12.34. A single driver can drive multiple source-terminated loads only under restricted conditions.

The trick to understanding this figure is to realize that the lines are coupled together into a jointly resonant structure. You cannot properly analyze just one line without seeing what happens to all the lines. The coupling happens because of the finite output impedance of the driver.

If the driver output impedance R S were zero (it never is), there would be no cross-coupling between lines, and you could simply use a separate series-terminating resistor of value R 1 = Z on each line. Unfortunately, the reality of finite driver impedance forces us to contemplate joint resonance . The paragraphs below show how to jointly analyze the system.

Skipping ahead to the answer, multiple source termination with a nonzero driver impedance works only if the lines are equally long and the loads at each end are balanced . The source-termination resistors must equal

Equation 12.6

 

where	R S = output resistance of driver, W ,
	Z = transmission line characteristic impedance, W ,
	R 1 = value of resistance added to each trace, and
	N = number of driven lines.

When driving one line ( N = 1), [12.6] matches the total source impedance ( R S + R 1 ) to the characteristic impedance Z . This is a normal source termination. When driving multiple lines, [12.6] prescribes smaller source-terminating resistors. With N too large, [12.6] goes negative, implying that no practical solution exists.

Let's analyze the lines in Figure 12.34 one at a time to see what happens. In Figure 12.34, a pulse travels down line A toward the load. This pulse reflects off the far end of line A, returning to the driver. In the usual application of source termination, the source termination matches the characteristic impedance of the line, eliminating the reflection at the driver. In Figure 12.34, however, the effective source impedance is not matched; it is set slightly lower than the characteristic impedance of the line. The returning pulse on line A therefore bounces off the driver, producing a negative reflection. So far, the negative reflection looks like a problem.

Another effect occurs at the same time. As current from the returning pulse on line A surges into the driver chip and through R S , it generates a voltage at the driver output pin. This voltage couples into line B. The polarity of the crosstalk pulse coupled onto line B is positive.

So far, the consequences of the returning reflected pulse on line A seem to include a negative reflection on line A and a positive crosstalk pulse on line B.

Now imagine what happens if the returning signals reflected off the far ends of lines A and B arrive at the same time. Each signal will induce on its own line a negative reflection and on the other line a positive amount of crosstalk. If you choose the resistor values carefully (according to [12.6]), you can get the negative reflection and positive crosstalk to cancel exactly. The result is a perfectly damped system.

The conditions under which perfect cancellation may be achieved are very restrictive :

• The lines must be equally long (this guarantees the reflected pulses will arrive at the same time).
• The loads must be balanced (this guarantees the reflected pulses will have the same shape).
• The resistors must be calculated according to [12.6].

Equation [12.6] sets the source-terminating resistance so that line A experiences a negative reflection pulse exactly compensated for by the positive crosstalk pulse from line B. Equation [12.6] works with any number of lines, as long as they are equal in length and identically loaded.

Perfect balance rarely occurs in practice. If the lines are not perfectly balanced, the reflections and crosstalk from each line will not cancel. Incomplete cancellation makes the system ring.

POINT TO REMEMBER

• A single driver can service two or more source-terminated lines only under limited conditions.

 

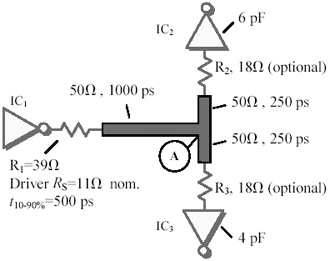
12.9.1 To Tee or Not To Tee

Article first published in EDN Magazine , February 2, 1998

The net topology shown in Figure 12.35 cannot be terminated satisfactorily. What I mean is, you can't simultaneously achieve these four objectives:

Figure 12.35. This topology, if all three branches are long compared to the signal rise (or fall) time, cannot be terminated satisfactorily.

• A crisp first incident wave,
• Of full size,
• With no residual reflections,
• That meets the demands of good circuit-design practice.

You can satisfy any combination of three, but not all four, of the above requirements.

[Ed. Note ”The following simulations were generated by HyperLynx software. The driver in each case is a simple 3.3-V CMOS model, with 10- W output impedances in both HI and LOW states, 6-nH package inductance (BGA), and a 1-ns rise/fall time (10% to 90%). All traces are 50- W configurations. Voltages shown are at the driver and receiver locations. Both receivers are the same, with a 3-pF input capacitance . A step-response waveform is shown on the left, and the first three cycles of a 66-MHz clock waveform on the right.]

The ground rules for this discussion are that all three branches of the circuit in Figure 12.35 are long compared to the length of a rising edge. In the simulations, the signal delay on each branch (1 ns) equals the signal rise and fall time (also 1 ns). Such a net, if left unterminated, displays nasty transmission-line characteristics like overshoot, undershoot, and ringing (Figure 12.36).

Figure 12.36. If left unterminated, the structure displays overshoot, undershoot, and ringing.

A slower driver improves the ratio of line delay to risetime, resulting in a better-damped waveform. For example, a 15-ns driver is slow enough to damp out the ringing and reflections, whether you terminate the line or not (Figure 12.37). Unfortunately, this approach gives up on the first criteria ”the response here is so slow, it won't work at 66 MHz.

Figure 12.37. A slower driver produces a better-damped waveform, but it's too slow to work at 66MHz.

Attenuation can sometimes help. For example, a combination of a 50- W series termination at A plus 50- W end terminations at both the receivers will damp all reflection modes (Figure 12.38). Unfortunately, this approach shrinks the received signal to only 1/3 of normal size. With specialized receivers, this architecture can work wonders. With ordinary single-ended logic receivers, the diminutive received signal is useless.

Figure 12.38. Appropriately-placed attenuating networks can damp all the oscillatory modes at the expense of shrinking the received signal to only 1/3 of normal size.

A weak termination will calm, but not totally cure, the ringing behavior. In Figure 12.39, weak terminations (100- W each) placed at each receiver improve the amplitude of the first incident wave, but after a while the reflections trapped between the low-impedance driver at A and the mismatch at junction B cause the received signal to overshoot, crest, and rattle about. It's not perfect, but at least in the steady-state condition the signal does eventually reach full amplitude.

Figure 12.39. A weak termination can help reduce, but totally cure, overshoot and ringing.

If you are willing to employ a sneaky trick, you can satisfy the first three conditions (Figure 12.40). This tricky circuit implements segment AB as a 50- W line while implementing segments BC and BD as 100- W lines (it takes really skinny microstrips to get this to work, but it's possible). When the signal from A hits junction B , it sees two 100- W loads in parallel, which is a good match for the 50- W segment AB . No reflections result. The signal at B cleaves perfectly, with half the current flowing down each path . One-hundred-ohm end-terminations at each receiver now perfectly terminate the whole net.

Figure 12.40. A sneaky adjustment of the characteristic impedance on each segment renders this net terminable.

Figure 12.40 looks pretty good, but it's not perfect yet. The little blip 4 ns into the step response at each receiver is caused by the parasitic capacitances of the receivers (set to 3-pF each for this simulation). This parasitic capacitance interferes with the action of the end termination, causing a reflection that eventually returns to haunt the received waveform. If you convert the topology into a source-terminated configuration, and if the line lengths are identical , even that tiny effect goes away. To implement this idea, set trace impedance AB to 50 W and traces BC and BD to 100 W . Apply a single 40- W series resistor at point A . The value of the resistor is calibrated so that its 40- W resistance plus the natural 10-ohm output impedance of driver equals the 50- W impedance of line (Figure 12.41). For this topology to work, segments BC and BD must be the same length.

Figure 12.41. The mixed-impedance idea combined with a source termination delivers almost perfect signals to the endpoints.

Figure 12.41 delivers the best-looking waveforms, but let me show you what goes wrong with source-termination if the trace lengths are not the same or if the loads are imbalanced . Using the same setup as in Figure 12.41, stretch the length of segment BC to 1.25 ns and shrink segment BD to 0.75 ns. That's a difference of only 0.500 ns, or 1/2 of a risetime, but it's enough to totally destroy the signal quality. In Figure 12.42 one of the two resulting received signals is shown. This system is pretty sensitive to delay, isn't it! The same general type of deterioration happens if you implement unbalanced gate capacitances.

Figure 12.42. The performance of this hairball network is sensitive to the balance between the line lengths leading to C and D.

Any time you connect up a hairball network like Figure 12.42, you should always check the performance assuming one gate is at its maximum input capacitance and line length while the other is at its minimum. Simulate with a risetime as fast as you anticipate seeing from any chip over the useful production life of the product.

An end-terminated topology, even using a weak end termination, is not quite so sensitive to delay as the source-terminated topology. This advantage accrues to the end-terminated topology because the end-termination impedances appear at the receivers in a position where they help prevent the signal from bouncing back and forth between C and D . In Figure 12.43 I retain the unbalanced line lengths (0.75 and 1.25 ns from BC and BD respectively), but revert to a 100- W termination at each endpoint and a direct hook-up (no resistor) at the driver.

Figure 12.43. The weak-end-terminator approach is not quite as sensitive to line-length imbalance.

Do any of these techniques constitute good design practice? That depends on your company's internal design procedures. Most companies do not have a good way to document, track, and enforce tricky high-speed design rules. For example, if you write a little thesis on your schematic about a high-speed design trick you've used, it's unlikely that your layout people will ever see it. It's not their job to read your schematic. It's their job to hook up the net list with the part footprints in their database and the standard design rules enforced in their shop at the time of layout. Even if you participate in the layout so it comes out perfectly, the next time your design is revised, it will get screwed up.

Unless you work with an integrated CAD system that automatically keeps track of tricky constraints, you should avoid the tee. Tricks like the tee circuit are too dangerous for practical use. A different approach, like splitting driver A into a pair of low-skew drivers with an independent point-to-point link to each load would remove the tricky constraints. A dual-driver topology is the kind of design that will work now and in the future when some kid who inherits your design tries to figure out what you did.

POINTS TO REMEMBER

• A slow driver can damp ringing, but it may need to be too slow for your circuit.
• Appropriately placed attenuating networks can damp all the oscillatory modes at the expense of shrinking the received signal.
• A weak termination can help reduce, but totally cure, overshoot and ringing.
• Test all combinations of maximum and minimum load capacitance and line length.
• Eventually, someone will inherit your hairball design and try to figure out what you did. Keep it simple.

 

12.9.2 Driving Two Loads

Article first published in EDN Magazine , July 19, 2001

The split-tee configuration (Figure 12.44, omitting R 2 and R 3 ) conveniently drives two CMOS receivers from one output. If you keep the stub traces connecting receivers IC 2 and IC 3 sufficiently short, the agglomeration of stubs and receivers at the end of the line acts as a single lumped-element capacitive load. Any reflections that bounce off this combination load return to the driver where source-terminating resistor R 1 extinguishes them. The receivers therefore see only one event in response to each step change at the driver. The heavy capacitance at the end of the line may affect the risetime of that event, but the result is monotonic with no lingering residual reflections.

Figure 12.44. The split-tee configuration drives two CMOS receivers from one output.

Sounds good, but how short must you keep the stubs? That decision depends on the risetime of the driver and the degree of balance between the load impedances. In general, I advocate limiting the stub delay to 1/6 the risetime, which usually works, but I always simulate it to make sure. The circuit also works with longer stubs, but as you stretch the limit, the circuit becomes increasingly susceptible to imbalance between the loads. Figure 12.45 illustrates the effect of such an imbalance.

Figure 12.45. Hidden within the split-tee is an unconstrained resonance.

Ignoring R 2 and R 3 for the moment, imagine you suddenly inject a positive step at IC 2 and a simultaneous negative step at IC 3 . The signal from IC 2 heads south toward IC 3 , while the signal at IC 3 heads north toward IC 2 . These two signals propagate toward each other, simultaneously crossing at point A . At this point, the voltages from the two signals, being opposite , perfectly cancel. No current couples onto the main trace at A . The two signals continue on their way, slamming into opposite ends of the stub traces, reflecting, and bouncing back and forth between IC 2 and IC 3 . I call this scenario an unconstrained resonance.

The mode is unconstrained because the terminator at IC 1 has no opportunity to damp these oscillations. As long as the system is perfectly balanced, the two opposite signals from IC 2 and IC 3 always perfectly cancel, coupling zero current onto the main trace. Resistor R 1 sees nothing. If the loads at IC 2 and IC 3 are perfectly reactive, the reflections may continue for many cycles. This circuit works like a child's seesaw. Imagine two kids furiously working the plank up and down. Standing at the fulcrum, you can't stop them. You have to stand near one end where the plank is moving to have any significant effect.

Hidden within every split-tee network is an unconstrained resonance.

 

Given zero coupling between the desired signal-propagation mode (current through R 1 ) and the IC 2 “IC 3 resonance, your signals should theoretically never excite the IC 2 “IC 3 resonance, so it should cause no problems. Unfortunately, zero coupling requires perfect balance between the load capacitances at IC 2 and IC 3 .

The circuit in Figure 12.44 is not perfectly balanced. Receiver IC 2 contributes 6 pF of loading, whereas receiver IC 3 contributes only 4 pF. The reflections between IC 2 and IC 3 therefore don't perfectly cancel. Coupling does occur between the current in R 1 and the IC 2 “IC 3 resonance, and the resulting received signals exhibit the horrible ringing shown in Figure 12.45 (the top traces assume R 2 = R 3 = 0). As you can see, the resonant mode occurs at about 500 MHz, corresponding to the third harmonic of the 166-MHz clock. As the clock starts, the heavy third overtone builds to ridiculous levels, causing nonmonotonic behavior and possibly double-clocking in the receivers.

To defeat the resonance, I've added 18- W resistors in series with each receiver. That's just enough in this example to knock down the Q of the highly resonant IC 2 “IC 3 mode, eliminating the wiggles in the output signal without unnecessarily degrading the received risetime (the bottom trace assume R 2 = R 3 = 18 W ).

Any time you build a split-tee, always simulate the circuit with a maximal degree of imbalance. For CMOS loads, that scenario means using the maximum load capacitance at one receiver and the minimum (sometimes zero) at the other. Look at the step response to see whether an observable resonance exists. If it does, simulate the circuit with a clock waveform at that resonant frequency (or 1/3 or 1/5 of that amount). Small series resistors in series with each gate input can sometimes extend the length at which the split-tee safely functions.

H-pattern distributions exhibit similar sensitivity to imbalance. The more symmetrical you make your layout and loading, the further you can stretch the lengths of the H-branches.

POINT TO REMEMBER

• Hidden within every split-tee network is an unconstrained resonance.