Two-Wire Circuits
Two-wire signaling cures many noise problems at the cost of a second signal trace. As shown in Figure 6.4, a two-wire transmitter sends current on two wires: a first wire, which carries the main signal, and a second wire, which is provided for the flow of returning signal current. As drawn, the currents on the two wires will be equal and opposite , but the voltages will not be. This architecture provides three important benefits.
Figure 6.4. Two-wire transmission provides a signal wire and return wire for each signal.
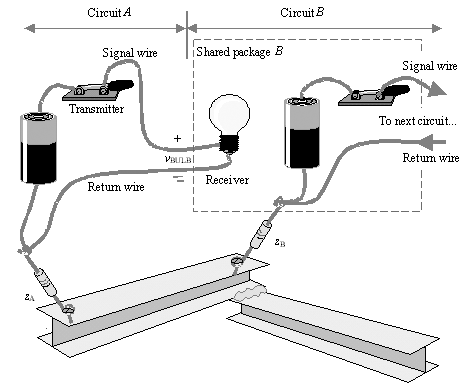
First, it frees the receiver from requiring a global reference voltage. [46] In effect, the second wire serves as a reference for the first. The receiver need merely look at the difference between the two incoming wires. Two-wire signaling renders a system immune to disturbances in distribution of global reference voltages, provided the disturbances do not exceed the power-supply noise tolerance of the logic family or the common-mode input range of the receivers.
[46] The reference voltage for TTL, most high-speed CMOS, and ECL is ground; for PECL (positively- biased ECL), it is the power voltage.
Second, the two-wire architecture eliminates shared-impedance coupling between a receiver and transmitter in the same package. In Figure 6.4, returning associated with transmitter B flows through the return wire back to the battery at B without traversing z B , and therefore without disturbing the receiver . By eliminating the shared-impedance coupling between circuits A and B , two-wire signaling conquers ground bounce locally generated within the package.
Third, two-wire signaling counteracts any type of interfering noise that affects both wires equally. A good example would be the ground shifts encountered in a high-speed connector. When two systems are mated by a connector, the net flow of signal current between the systems returns to its source through the ground (or power) pins of the connector. As it does so, tiny voltages are induced across the inductance of the connector's ground (or power) pins. These tiny voltages appear as a difference between the ground (or power) voltage on one side of the connector and the ground (or power) voltage on the other side. This problem is called a ground shift , and it is yet another form of common impedance coupling. Two-wire signaling fixes this problem.
These three benefits do not depend on the use of any changing voltage on the second wire. As shown in Figure 6.4, the return wire merely carries the local reference voltage (ground, in this case) from the transmitter to the receiver, where it may be observed . This simple circuit renders the system immune to local disturbances in the power and ground voltages, ground bounce generated within a package, and ground bounce generated within a connector. That's pretty good.
The performance of a two-wire signaling circuit hinges on the assumption that no current flows through impedances z A and z B . Under this assumption the receiver at B can directly observe (on the return wire) the local reference voltage at transmitter A , and the next receiver C can observe the local reference voltage at transmitter B . Any currents flowing through z A or z B change the references voltages on the return wires, interfering with reception . The two-wire circuit must be arranged so that it limits the current through z A and z B to innocuous levels.
Unfortunately, in a high-speed system all wires couple to the surrounding chassis and other metallic objects, whether you want them to or not. In Figure 6.4 you can model this coupling as a collection of parasitic lumped-element connections connected from each wire to the reference beam. Current transmitted on the signal wire therefore has a choice of returning pathways . It can return to the source along the return wire (the intended path ), or it can flow through the parasitic connection to the reference beam and from there return to the transmitter through impedance z A . The current that flows through the parasitic pathway is called stray returning signal current . At high speeds the stray returning signal current is often significant enough to impair the effectiveness of a two-wire signaling system.
Does this impairment defeat the utility of two-wire signaling for high-speed circuits? Not necessarily , provided that you pick a particular, unique signal for the second wire. The second wire must carry a signal equal in amplitude to the first, but opposite in polarity (an antipodal , or complementary , signal). If you do that, everything still works.
POINTS TO REMEMBER
- Two-wire signaling renders a system immune to disturbances in distribution of global reference voltages.
- Two-wire signaling counteracts any type of interfering noise that affects both wires equally.
- Two-wire signaling counteracts ground bounce (also called simultaneous switching noise) within a receiver.
- Two-wire signaling counteracts ground shifts in connectors.
- Two-wire signaling works when there is no significant stray returning signal current.
Fundamentals
- Impedance of Linear, Time-Invariant, Lumped-Element Circuits
- Power Ratios
- Rules of Scaling
- The Concept of Resonance
- Extra for Experts: Maximal Linear System Response to a Digital Input
Transmission Line Parameters
- Transmission Line Parameters
- Telegraphers Equations
- Derivation of Telegraphers Equations
- Ideal Transmission Line
- DC Resistance
- DC Conductance
- Skin Effect
- Skin-Effect Inductance
- Modeling Internal Impedance
- Concentric-Ring Skin-Effect Model
- Proximity Effect
- Surface Roughness
- Dielectric Effects
- Impedance in Series with the Return Path
- Slow-Wave Mode On-Chip
Performance Regions
- Performance Regions
- Signal Propagation Model
- Hierarchy of Regions
- Necessary Mathematics: Input Impedance and Transfer Function
- Lumped-Element Region
- RC Region
- LC Region (Constant-Loss Region)
- Skin-Effect Region
- Dielectric Loss Region
- Waveguide Dispersion Region
- Summary of Breakpoints Between Regions
- Equivalence Principle for Transmission Media
- Scaling Copper Transmission Media
- Scaling Multimode Fiber-Optic Cables
- Linear Equalization: Long Backplane Trace Example
- Adaptive Equalization: Accelerant Networks Transceiver
Frequency-Domain Modeling
- Frequency-Domain Modeling
- Going Nonlinear
- Approximations to the Fourier Transform
- Discrete Time Mapping
- Other Limitations of the FFT
- Normalizing the Output of an FFT Routine
- Useful Fourier Transform-Pairs
- Effect of Inadequate Sampling Rate
- Implementation of Frequency-Domain Simulation
- Embellishments
- Checking the Output of Your FFT Routine
Pcb (printed-circuit board) Traces
- Pcb (printed-circuit board) Traces
- Pcb Signal Propagation
- Limits to Attainable Distance
- Pcb Noise and Interference
- Pcb Connectors
- Modeling Vias
- The Future of On-Chip Interconnections
Differential Signaling
- Differential Signaling
- Single-Ended Circuits
- Two-Wire Circuits
- Differential Signaling
- Differential and Common-Mode Voltages and Currents
- Differential and Common-Mode Velocity
- Common-Mode Balance
- Common-Mode Range
- Differential to Common-Mode Conversion
- Differential Impedance
- Pcb Configurations
- Pcb Applications
- Intercabinet Applications
- LVDS Signaling
Generic Building-Cabling Standards
- Generic Building-Cabling Standards
- Generic Cabling Architecture
- SNR Budgeting
- Glossary of Cabling Terms
- Preferred Cable Combinations
- FAQ: Building-Cabling Practices
- Crossover Wiring
- Plenum-Rated Cables
- Laying Cables in an Uncooled Attic Space
- FAQ: Older Cable Types
100-Ohm Balanced Twisted-Pair Cabling
- 100-Ohm Balanced Twisted-Pair Cabling
- UTP Signal Propagation
- UTP Transmission Example: 10BASE-T
- UTP Noise and Interference
- UTP Connectors
- Issues with Screening
- Category-3 UTP at Elevated Temperature
150-Ohm STP-A Cabling
- 150-Ohm STP-A Cabling
- 150- W STP-A Signal Propagation
- 150- W STP-A Noise and Interference
- 150- W STP-A: Skew
- 150- W STP-A: Radiation and Safety
- 150- W STP-A: Comparison with UTP
- 150- W STP-A Connectors
Coaxial Cabling
- Coaxial Cabling
- Coaxial Signal Propagation
- Coaxial Cable Noise and Interference
- Coaxial Cable Connectors
Fiber-Optic Cabling
- Fiber-Optic Cabling
- Making Glass Fiber
- Finished Core Specifications
- Cabling the Fiber
- Wavelengths of Operation
- Multimode Glass Fiber-Optic Cabling
- Single-Mode Fiber-Optic Cabling
Clock Distribution
- Clock Distribution
- Extra Fries, Please
- Arithmetic of Clock Skew
- Clock Repeaters
- Stripline vs. Microstrip Delay
- Importance of Terminating Clock Lines
- Effect of Clock Receiver Thresholds
- Effect of Split Termination
- Intentional Delay Adjustments
- Driving Multiple Loads with Source Termination
- Daisy-Chain Clock Distribution
- The Jitters
- Power Supply Filtering for Clock Sources, Repeaters, and PLL Circuits
- Intentional Clock Modulation
- Reduced-Voltage Signaling
- Controlling Crosstalk on Clock Lines
- Reducing Emissions
Time-Domain Simulation Tools and Methods
- Ringing in a New Era
- Signal Integrity Simulation Process
- The Underlying Simulation Engine
- IBIS (I/O Buffer Information Specification)
- IBIS: History and Future Direction
- IBIS: Issues with Interpolation
- IBIS: Issues with SSO Noise
- Nature of EMC Work
- Power and Ground Resonance
Points to Remember
Appendix A. Building a Signal Integrity Department
Appendix B. Calculation of Loss Slope
Appendix C. Two-Port Analysis
- Appendix C. Two-Port Analysis
- Simple Cases Involving Transmission Lines
- Fully Configured Transmission Line
- Complicated Configurations
Appendix D. Accuracy of Pi Model
Appendix E. erf( )
Notes
EAN: N/A
Pages: 163
- The Second Wave ERP Market: An Australian Viewpoint
- Distributed Data Warehouse for Geo-spatial Services
- Healthcare Information: From Administrative to Practice Databases
- Relevance and Micro-Relevance for the Professional as Determinants of IT-Diffusion and IT-Use in Healthcare
- Development of Interactive Web Sites to Enhance Police/Community Relations
