Derivation of Telegraphers Equations
Derivation of Telegrapher s Equations
The telegrapher's discrete equivalent circuit model for a continuous transmission line appears in Figure 2.3. This model breaks the transmission line into a cascade of small segments or blocks of a standard length. Each model comprises a series impedance z and a shunt admittance y .
Figure 2.3. Series impedance z consists of resistor R in combination with inductor L ; shunt admittance y consists of conductance G in parallel with capacitor C.
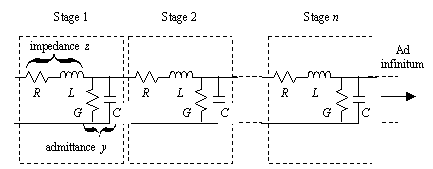
The series impedance z consists of a resistor R in combination with an inductor L . The shunt admittance y consists of a conductance G in parallel with a capacitor C . Each of the values R , L , G , and C represent the cumulative amount of resistance, inductance, capacitance , or conductance measured per unit length in the transmission line, where the standard of measurement conforms to the size of the blocks in Figure 2.3. The standard length is traditionally set in units related to the size of the transmission structure. For example, in pcb problems the standard length might be inches or mm, whereas in a power-transmission problem the standard length would more likely be miles or km. Provided that you maintain the same units consistently throughout your calculations, the standard unit of length becomes irrelevant in the final formulas for impedance and transmission loss. For the sake of concreteness this book employs a unit length of one meter.
The telegrapher's equations may be derived from the cascaded lumped-element equivalent circuit model. I like deriving the equations this way because ladder circuits are fairly easy to analyze and don't require the use of partial differential equations. The two transmission-line quantities of most importance that may be gleaned from the telegrapher's equations are the input impedance Z C and transfer coefficient g (gamma).
2.2.1 Definition of Characteristic Impedance Z C
Let the symbol Z C represent the characteristic impedance of a transmission line. Characteristic impedance is defined mathematically as the ratio of voltage to current experienced by a signal traveling in one direction along a transmission line. At every point within such a traveling waveform the incremental amounts of voltage v and current i caused by that waveform bear the same relationship to one another, v / i = Z C . The quantity Z C is a function of frequency.
In this book the variable Z is interpreted as a single-valued constant showing the value of characteristic impedance at some particular frequency w (as in the expression Z = 50 W ). The variable Z C is reserved as an expression for the characteristic impedance as a function of frequency, usually but not always shown as Z C ( w ).
The characteristic impedance Z C of a transmission line does not in general equal its input impedance Z in . The difficulty with relating Z C to Z in is that transmission lines support (at least) two modes of signal flow. These modes include a signal moving to the right and a signal moving to the left. Both modes co-exist, superimposed on top of each other. Within the traveling components of each individual mode the voltage and current always bear the proper relationship, but where the modes cross the ratio of total voltage to total current can take on any value.
What you need to remember about Z in and Z C are three facts:
- Lacking any intentional (or reflected) signals emanating from the far end of a transmission line (i.e., when there is only one mode of signal flow), Z in equals Z C .
- If reflections are present, the correlation between Z in and Z C evaporates.
- Only under special circumstances where there are no reflections can you infer Z C from measurements of Z in .
The typical procedure for measuring characteristic impedance uses a time-domain reflectometer (TDR). The TDR setup injects a rising or falling edge of known open -circuit amplitude v and known source impedance Z S into the transmission line under test while observing the signal coupled into the input of the transmission line (Figure 2.4). Provided that the rise (or fall) time of the measuring apparatus completes well before one round-trip delay of the transmission line, the observed signal will achieve some steady-state value a prior to the arrival of the first reflections from the far end of the line. The ratio of a to v indicates the input impedance of the structure, which under the circumstances stated should equal the characteristic impedance of the transmission line.
Equation 2.1
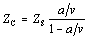
|
where |
a is the steady-state step amplitude of the measured signal ( V ), |
|
v is the open-circuit voltage of the step source ( V ), |
|
|
Z S is the output impedance of the step source ( W ), and |
|
|
Z C is the characteristic impedance of the transmission line ( W ). |
Figure 2.4. A simple TDR experiment observes the transmission line while injecting a step of known amplitude and source impedance.
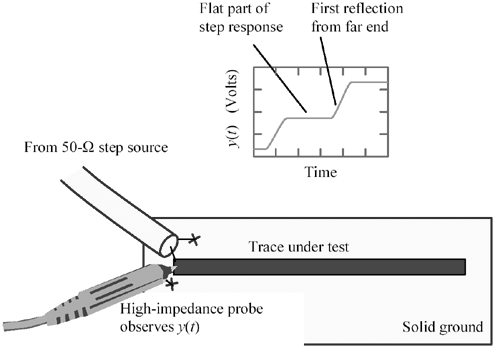
Professional-quality TDR instruments conduct their observations from a point near the source end of the 50- W cable, but the principle remains the same.
When injecting a step into a line of finite length, the front end of the line initially experiences only one mode of signal transmission (excepting any static initial conditions), so the line temporarily displays an input impedance equal to Z C . After one round-trip delay, reflections may arrive from the far end. The reflections and the resulting measured input impedance will then depend on the configuration of the load at the far end of the line ”hence your measurement of Z C must be completed prior to the arrival of the first reflection.
POINT TO REMEMBER
- The telegrapher's equations are derived from a cascaded lumped-element equivalent circuit model.
2.2.2 Changes in Characteristic Impedance
This brief discussion of characteristic impedance has so far glossed over an important point, namely, that the characteristic impedance Z C may change as a function of frequency. In that case the measured step-response waveform will not display a perfectly flat top, and you must get into the business of deciding where along a sloping waveform to pick the one true point from which to calculate the characteristic impedance. You should know that there is no good way to determine such a point. Your only recourse is to loosely relate the characteristic impedance at frequency w (rad/s) to the step-response amplitude averaged over an interval of time equal to 1/ w .
Fortunately, in typical digital transmission situations on pcbs the impedance changes fairly slowly over the relevant frequency range. An adequate measurement of characteristic impedance may usually be made using a step source with a rise time comparable to the rise time of the circuits that will be used in your actual system and taking the step amplitude at a point two or three rise times away from the step edge.
Thin-film structures and flex-circuits with very fine traces may posses sufficient series resistance to cause the characteristic impedance to vary noticeably with frequency (see Section 3.6.3, "Influence of Series Resistance on TDR Measurements"). Also, long or high-resistance transmission lines operated in the RC mode show a noticeable variation of characteristic impedance with freqeuncy (see Section 3.5, "RC Region").
POINT TO REMEMBER
- In typical digital transmission situations on pcbs the characteristic impedance changes fairly slowly over the relevant frequency range.
2.2.3 Calculation of Impedance Z c From Parameters R, L, G, And C
The lumped-element derivation for Z C begins by clumping together the series impedance and shunt admittance of each block into the summary terms z and y respectively. Both quantities vary with frequency.
Equation 2.2
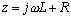
Equation 2.3
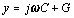
Consider first the input impedance of an infinite chain of cascaded blocks (Figure 2.3). Common sense tells you that adding one more block to the front of the infinite chain won't change the input impedance 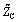 of the whole structure. You can use this principle to deduce
of the whole structure. You can use this principle to deduce 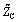 . The tilde over the symbol Z exists to remind you that the following discussion concerns the input impedance of an infinite chain of discrete blocks, a slightly different concept than the characteristic impedance of a continuous transmission line.
. The tilde over the symbol Z exists to remind you that the following discussion concerns the input impedance of an infinite chain of discrete blocks, a slightly different concept than the characteristic impedance of a continuous transmission line.
Mathematically, the addition of a new block to the front end of the chain comprises two steps, first combining a shunt admittance y in parallel with 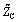 and then supplementing that result by adding series impedance z . The result should, according to our common-sense logic, reproduce
and then supplementing that result by adding series impedance z . The result should, according to our common-sense logic, reproduce 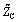 .
.
Equation 2.4
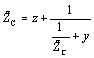
Multiply both sides by  .
.
Equation 2.5
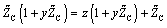
Cancel out the two linear 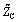 terms.
terms.
Equation 2.6
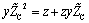
Divide both sides by y and then take the square root of both sides.
Equation 2.7
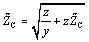
Equation [2.7] expresses the input impedance of an infinite chain of discrete lumped-element blocks. Of course, a cascade of lumped-element circuit blocks only approximates the behavior of a continuous transmission line, but the approximation works better and better as the size (length) of each block shrinks and the number of blocks increases . In practical situations the discrete model works well when the delay of each block shrinks to less than the rise or fall time of the signals involved. In the limit as the block size approaches zero, the discrete model becomes perfect.
Splitting each block from Figure 2.3 into a cascade of n blocks changes the values of R , L , G , and C within each block to new values R/n , L/n , G/n , and C/n , respectively. These changes modify z and y to produce new values z/n and y/n . Substituting the new values into [2.7] and taking the limit as n approaches infinity produces an equation for the input impedance of a continuous transmission line.
Equation 2.8
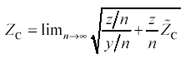
In the limit the right-hand term under the radical plummets to insignificance, leaving you with a fixed expression for Z C .
Equation 2.9
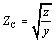
This expression may become more recognizable if you substitute [2.2] and [2.3] for z and y :
Equation 2.10
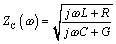
In general the value of Z C varies significantly with frequency. You may notice that by setting time constant L / R exactly equal to C / G , both impedance and line loss remain constant at all frequencies. Such an arrangement is called a "constant loss" configuration. This special case is rarely attempted in practice. In practical modern transmission lines the G term hovers near zero while R changes noticeably with frequency, rendering any convergence of L / R and C / G virtually impossible .
As you go to higher and higher frequencies, however, the terms R and G may eventually be neglected as they are overwhelmed by j w L and j w C respectively, leading to a steady plateau in impedance. The fine balance between the inductive impedance j w L and the capacitive admittance j w C holds the impedance constant at high frequencies. This constant-impedance plateau greatly aids the design of high-speed digital circuits, as it makes possible the termination of transmission lines with a single resistor. [8] The value of characteristic impedance at the plateau is called Z .
[8] Exceptions to this rule include most on-chip interconnects, for which the term R looms so great that practical operating frequencies may never reach the constant-impedance plateau. Fortunately, these lines operate in a dispersive mode that rarely requires termination.
Equation 2.11
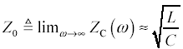
I should make some careful remarks about the usage of the limit in [2.11]. Given the form of the expression [2.10], the limit is appropriate. In real-world applications, however, at very high frequencies the simple model of [2.10] no longer applies, as the circuit becomes overwhelmed by multiple non-TEM modes of propagation, also known as waveguide modes. Therefore, the variable Z must be interpreted here as a single-valued constant (as in the expression Z = 50 W ) only when evaluated at some frequency w that lies above the LC and skin-effect mode onset frequencies (so that R and G are negligible in [2.10]), but below the onset of multiple waveguide modes of operation. Within this region the characteristic impedance is relatively flat with frequency, and it makes sense to talk about a single value of characteristic impedance Z . Wherever you see the expression Z , remember it is an approximation that applies only within a limited range of frequencies.
The variable Z C is reserved as an expression for the characteristic impedance as a function of frequency, usually but not always shown as Z C ( w ).
POINT TO REMEMBER
- At frequencies above the LC and skin-effect mode onset, but below the onset of multiple waveguide modes of operation, the characteristic impedance is relatively flat and
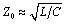
2.2.4 Definition of Propagation Coefficient g
Signals propagating along a transmission structure are attenuated by a certain factor H as they pass through each unit length of the line. [9] The attenuation factor H in each section is the same. The signal amplitude therefore decays exponentially with distance.
[9] This analysis assumes the line operates in a linear, time-invariant fashion, which most structures do for all reasonable digital signal amplitudes.
The per-unit-length attenuation factor H is called the propagation function of a transmission line. It varies with frequency. Let the symbol H ( w ) represent the curve of attenuation versus frequency w in a unit-length segment, and the symbol H ( w , l ), the same curve in a line of length l . H ( w , l ) relates exponentially to H ( w ).
Equation 2.12

Equation [2.12] works for integral as well as fractional l .
Since the response is exponential, why not take a look at the complex logarithm of H ( w )? From the complex logarithm, you can always reconstruct the original value:
Equation 2.13
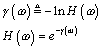
The negative sign in the definition of g appears in anticipation of working with attenuating functions, so that the real part of g remains positive. [10] The (negative) natural logarithm of the per-unit-length propagation function H is given the name propagation coefficient . Its units are complex nepers per meter. The term neper means natural logarithm of the magnitude. The advantage of working with logarithms is that the logarithmic response scales linearly with l , simplifying certain of our calculations.
[10] Transmission lines generally attenuate their signals unless you are using an amplifying transmission media like a maser, laser, or Erbium-doped optical amplifier .
Equation 2.14
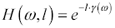
The logarithmic substitution is further broken down by defining a and b as the real and imaginary parts of g .
Equation 2.15
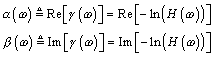
Separating the real and imaginary parts of the natural logarithm emphasizes their independent nature. Coefficient a specifies the attenuation induced by H , and b , the phase delay . Restated in terms of the propagation coefficient, the real part of g controls the magnitude of H , and the imaginary part controls the phase (see [2.16]).
The variable a (real part of g ) is expressed in units of nepers per unit length. An attenuation of one neper per unit length ( a = 1) equals “8.6858896 dB of gain per unit length. This amount of attenuation scales a signal by 1/ e as it passes through each unit length of transmission line.
The variable b (imaginary part of g ) is expressed in units of radians per unit length. A phase delay of one radian per unit length ( b = 1) equals “57.295779 degrees of phase shift per unit length. After 2 p lengths of line, a signal with this amount of phase delay is rotated back to its original phase.
Parameters a , b , and g all vary with frequency. When these variables appear without their frequency arguments, you are expected to remember that a variation with frequency is still implied .
Sometimes it is convenient to work with a or b individually.
Equation 2.16
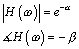
Combining [2.14] and [2.15] you may now express the complete one-way transfer function H ( w , l ) of a line of length l as a function of its complex logarithm.
Equation 2.17
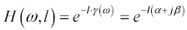
POINTS TO REMEMBER
- Signals propagating on a transmission line decay exponentially with distance.
- The per-unit-length attenuation factor H ( w ) is called the propagation function of a transmission line.
- The propagation coefficient g ( w ) is defined as the (negative of the) natural logarithm of H ( w ).
- The propagation coefficient g ( w ) may be broken down into its real and imaginary parts ( a and b ).
- The real part of g ( w ) defines the attenuation per unit length of a transmission structure in nepers per unit length.
- The imaginary part g ( w ) defines the phase shift per unit length of a transmission structure in radians per unit length.
2.2.5 Calculation of Propagation Coefficient g from Parameters R , L , G , and C
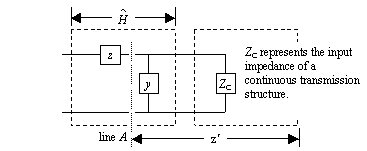
Figure 2.5 adds one unit- sized discrete transmission block to the head of a long, continuous transmission line with input impedance Z C . Defining z' as the impedance looking to the right of line A , the resistor-divider theorem computes the transmission coefficient 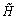 .
.
Figure 2.5. Define z' as the impedance of everything to the right of line A .
Equation 2.18
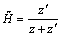
The term z' equals the parallel combination of admittance y and impedance Z C , where the impedance Z C is defined in the limit of small block size by [2.9]. Making this substitution into [2.18],
Equation 2.19
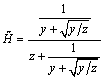
Multiply top and bottom by 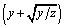 .
.
Equation 2.20
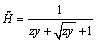
Equation [2.20] expresses the transfer function of one discrete block of unit size. As before, an individual discrete block only approximates the behavior of a continuous transmission line, so I will again take a limit as I split the single unit-sized block into a succession of n blocks, each of length 1/ n . This change modifies z and y in [2.20] to produce new values z/n and y/n . The combined response of the cascade of n blocks equals the response of an individual block of size 1/ n raised to the n th power.
Equation 2.21
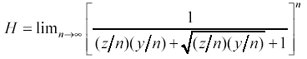
Simplify this expression by inverting the fraction, negating the exponent, and dividing out the common term n from part of the denominator.
Equation 2.22

Next you need a well-known mathematical fact [25] .
Equation 2.23
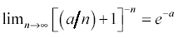
In equation [2.22] the expression 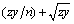 plays the role of a in [2.23]. The final form of the result takes the limit as n approaches infinity, forcing the first part of the expression zy/n towards zero, leaving only
plays the role of a in [2.23]. The final form of the result takes the limit as n approaches infinity, forcing the first part of the expression zy/n towards zero, leaving only 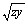 to go into the exponent.
to go into the exponent.
Equation 2.24
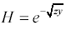
From [2.24] you may extract the propagation coefficient g .
Equation 2.25
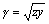
This expression may become more recognizable if you substitute [2.2] and [2.3] for z and y :
Equation 2.26
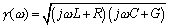
The factor  is called the propagation coefficient of the transmission line. The propagation coefficient may be subdivided into its real and imaginary parts,
is called the propagation coefficient of the transmission line. The propagation coefficient may be subdivided into its real and imaginary parts, 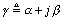 , where a denotes the attenuation, in nepers per unit length, and b denotes the phase delay in radians per unit length. Both a and b vary with frequency.
, where a denotes the attenuation, in nepers per unit length, and b denotes the phase delay in radians per unit length. Both a and b vary with frequency.
The final form of the telegrapher's equation predicts, given R , L , G , and C , the amplitude and phase response for a single mode of propagation on any transmission line.
Equation 2.27
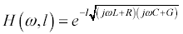
The trick to successfully modeling transmission structures lies not merely in understanding the telegrapher's equation, but in understanding what compromises and simplifications you can make in deriving useful approximations for the basic line parameters R , L , G , and C . The remainder of this chapter discusses the calculation of basic line parameters.
POINT TO REMEMBER
- The propagation coefficient
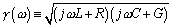 .
.
Fundamentals
- Impedance of Linear, Time-Invariant, Lumped-Element Circuits
- Power Ratios
- Rules of Scaling
- The Concept of Resonance
- Extra for Experts: Maximal Linear System Response to a Digital Input
Transmission Line Parameters
- Transmission Line Parameters
- Telegraphers Equations
- Derivation of Telegraphers Equations
- Ideal Transmission Line
- DC Resistance
- DC Conductance
- Skin Effect
- Skin-Effect Inductance
- Modeling Internal Impedance
- Concentric-Ring Skin-Effect Model
- Proximity Effect
- Surface Roughness
- Dielectric Effects
- Impedance in Series with the Return Path
- Slow-Wave Mode On-Chip
Performance Regions
- Performance Regions
- Signal Propagation Model
- Hierarchy of Regions
- Necessary Mathematics: Input Impedance and Transfer Function
- Lumped-Element Region
- RC Region
- LC Region (Constant-Loss Region)
- Skin-Effect Region
- Dielectric Loss Region
- Waveguide Dispersion Region
- Summary of Breakpoints Between Regions
- Equivalence Principle for Transmission Media
- Scaling Copper Transmission Media
- Scaling Multimode Fiber-Optic Cables
- Linear Equalization: Long Backplane Trace Example
- Adaptive Equalization: Accelerant Networks Transceiver
Frequency-Domain Modeling
- Frequency-Domain Modeling
- Going Nonlinear
- Approximations to the Fourier Transform
- Discrete Time Mapping
- Other Limitations of the FFT
- Normalizing the Output of an FFT Routine
- Useful Fourier Transform-Pairs
- Effect of Inadequate Sampling Rate
- Implementation of Frequency-Domain Simulation
- Embellishments
- Checking the Output of Your FFT Routine
Pcb (printed-circuit board) Traces
- Pcb (printed-circuit board) Traces
- Pcb Signal Propagation
- Limits to Attainable Distance
- Pcb Noise and Interference
- Pcb Connectors
- Modeling Vias
- The Future of On-Chip Interconnections
Differential Signaling
- Differential Signaling
- Single-Ended Circuits
- Two-Wire Circuits
- Differential Signaling
- Differential and Common-Mode Voltages and Currents
- Differential and Common-Mode Velocity
- Common-Mode Balance
- Common-Mode Range
- Differential to Common-Mode Conversion
- Differential Impedance
- Pcb Configurations
- Pcb Applications
- Intercabinet Applications
- LVDS Signaling
Generic Building-Cabling Standards
- Generic Building-Cabling Standards
- Generic Cabling Architecture
- SNR Budgeting
- Glossary of Cabling Terms
- Preferred Cable Combinations
- FAQ: Building-Cabling Practices
- Crossover Wiring
- Plenum-Rated Cables
- Laying Cables in an Uncooled Attic Space
- FAQ: Older Cable Types
100-Ohm Balanced Twisted-Pair Cabling
- 100-Ohm Balanced Twisted-Pair Cabling
- UTP Signal Propagation
- UTP Transmission Example: 10BASE-T
- UTP Noise and Interference
- UTP Connectors
- Issues with Screening
- Category-3 UTP at Elevated Temperature
150-Ohm STP-A Cabling
- 150-Ohm STP-A Cabling
- 150- W STP-A Signal Propagation
- 150- W STP-A Noise and Interference
- 150- W STP-A: Skew
- 150- W STP-A: Radiation and Safety
- 150- W STP-A: Comparison with UTP
- 150- W STP-A Connectors
Coaxial Cabling
- Coaxial Cabling
- Coaxial Signal Propagation
- Coaxial Cable Noise and Interference
- Coaxial Cable Connectors
Fiber-Optic Cabling
- Fiber-Optic Cabling
- Making Glass Fiber
- Finished Core Specifications
- Cabling the Fiber
- Wavelengths of Operation
- Multimode Glass Fiber-Optic Cabling
- Single-Mode Fiber-Optic Cabling
Clock Distribution
- Clock Distribution
- Extra Fries, Please
- Arithmetic of Clock Skew
- Clock Repeaters
- Stripline vs. Microstrip Delay
- Importance of Terminating Clock Lines
- Effect of Clock Receiver Thresholds
- Effect of Split Termination
- Intentional Delay Adjustments
- Driving Multiple Loads with Source Termination
- Daisy-Chain Clock Distribution
- The Jitters
- Power Supply Filtering for Clock Sources, Repeaters, and PLL Circuits
- Intentional Clock Modulation
- Reduced-Voltage Signaling
- Controlling Crosstalk on Clock Lines
- Reducing Emissions
Time-Domain Simulation Tools and Methods
- Ringing in a New Era
- Signal Integrity Simulation Process
- The Underlying Simulation Engine
- IBIS (I/O Buffer Information Specification)
- IBIS: History and Future Direction
- IBIS: Issues with Interpolation
- IBIS: Issues with SSO Noise
- Nature of EMC Work
- Power and Ground Resonance
Points to Remember
Appendix A. Building a Signal Integrity Department
Appendix B. Calculation of Loss Slope
Appendix C. Two-Port Analysis
- Appendix C. Two-Port Analysis
- Simple Cases Involving Transmission Lines
- Fully Configured Transmission Line
- Complicated Configurations
Appendix D. Accuracy of Pi Model
Appendix E. erf( )
Notes
EAN: N/A
Pages: 163
- Chapter I e-Search: A Conceptual Framework of Online Consumer Behavior
- Chapter III Two Models of Online Patronage: Why Do Consumers Shop on the Internet?
- Chapter IV How Consumers Think About Interactive Aspects of Web Advertising
- Chapter XVI Turning Web Surfers into Loyal Customers: Cognitive Lock-In Through Interface Design and Web Site Usability
- Chapter XVII Internet Markets and E-Loyalty
