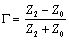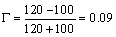Differential Impedance

What is differential impedance? Differential impedance is the ratio of voltage to current on a pair of transmission lines when driven in the differential mode (one signal positive and the other negative).

For example, the circuit in Figure 6.10 drives a signal x ( t ) differentially into a pair of uncoupled transmission lines [48] . Because the lines are symmetrical, the voltage splits evenly and you see voltage ½ x ( t ) on the top line and - ½ x ( t ) on the bottom. The current through each load must therefore equal ½ x ( t )/ Z . This current flows through both lines, and through both loads, in the direction shown.

[48] Traces separated by more than four times the trace height h interact so slightly that for purposes of impedance analysis, one usually ignores the effect of one on the other. Such traces are said to be uncoupled . The exact degree of separation required to produce an inconsequential interaction of course depends upon what you consider to be inconsequential.

Figure 6.10. The differential input impedance of a pair of noninteracting transmission lines is 2 Z .

The differential impedance (ratio of differential voltage to current) is

Equation 6.13

 

where	Z DIFF is the differential impedance of a pair of uncoupled transmission lines ( W ),
	Z is the characteristic impedance of either line alone, also called the uncoupled impedance ( W ),
	x ( t ) is the differential voltage applied across both lines (V), and
	½ x ( t )/ Z is the current driven into each line by the source (A).

The differential impedance of two matched, noninteracting transmission lines is double the impedance of either line alone .

If the lines are coupled , the situation changes. As an example of coupling , think of two parallel pcb traces. These traces will always exhibit some (perhaps very small) level of crosstalk. In other words, the voltages and currents on one line affect the voltages and currents on the other. In that way the two transmission lines are coupled together.

With a pair of coupled traces, the current on either trace depends in part on crosstalk from the other. For example, when both traces carry the same signal, the polarity of crosstalk is positive, which reduces the current required on either trace. When the traces carry complementary signals, the crosstalk is negative, which increases the current required on either trace. Figure 6.11 illustrates the situation. The characteristic impedance of each line to ground (including consideration of the adjacent trace) is represented as a single lumped-element component Z 1 . The impedance coupling the two transmission lines is depicted as a single lumped-element device Z 2 .

Figure 6.11. Driving point impedance of two different two-wire scenarios.

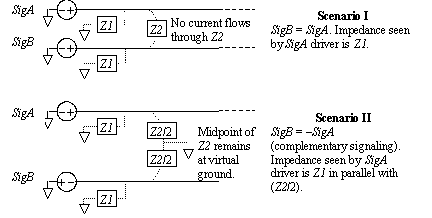
In the first scenario SigB is driven identically with SigA . The voltages on the two wires are therefore the same at all points in time, so (conceptually) no current flows through the coupling impedance Z 2 . The impedance (ratio of voltage to current) measured for each wire under this condition equals Z 1 . This is called the even-mode impedance of the transmission structure.

In the second scenario SigA and SigB are driven with complementary signals. This is called differential signaling, or sometimes antipodal signaling. Under these conditions the midpoint of impedance Z 2 remains at a virtual ground. An AC analysis of this circuit reveals that the impedance measured for each wire under this condition equals Z 1 in parallel with half of Z 2 . This value of impedance is called the odd-mode impedance. The odd-mode impedance is always less than the even-mode impedance .

The terms even-mode impedance and odd-mode impedance are closely related to the terms common-mode impedance and differential-mode impedance . Common-mode impedance is measured with the two wires driven in parallel from a common source. Common-mode impedance is by definition half the even-mode impedance.

Differential-mode impedance is twice the odd-mode impedance. It is measured using a well-balanced source, computing the ratio of the differential voltage (twice the odd-mode voltage) to the current on either line.

Combining your knowledge about common and differential mode impedances, you should be able to prove that the common-mode impedance always exceeds one-fourth of the differential-mode impedance.

Just as an example, suppose we have two 50-ohm, uncoupled transmission lines. As long as the lines are far enough apart to remain uncoupled, the even-mode and odd-mode impedances for these two lines will be the same, and equal to 50 ohms. Should you connect these two lines in parallel, the common-mode impedance would be 25 ohms. Should you connect these two lines to a differential source, the differential input impedance of the pair of lines would be 100 ohms.

POINTS TO REMEMBER

• Differential impedance is the impedance measured between two conductors when they are driven in the differential mode.
• Odd-mode impedance is the impedance measured on either of two conductors when they are driven with opposite signals in the differential mode.
• The value of differential-mode impedance is twice the value of odd-mode impedance.
• The differential impedance of two matched, uncoupled transmission lines is double the impedance of either line alone.
• The odd-mode impedance of two matched, uncoupled transmission lines equals the impedance of either line alone.
• Coupling between two parallel pcb traces decreases both differential and odd-mode impedances.
• Common-mode impedance is the impedance measured on two wires in parallel when they are driven together.
• Even-mode impedance is the impedance measured on either of two wires when they are driven with identical signals in the common mode.
• The value of common-mode impedance is half the value of even-mode impedance.

 

6.9.1 Relation Between Odd-Mode and Uncoupled Impedance

I should now like to discuss the relation between the odd-mode impedance and the uncoupled impedance . The uncoupled impedance Z C is what you would measure if the same transmission lines were widely separated, so they couldn't interact. What you need to know is simple: The odd-mode impedance of a coupled transmission line is always less than the uncoupled impedance. The even-mode impedance is always greater . The closer you place the line, the more coupling you will induce, and the greater a discrepancy you will see between the odd-mode, uncoupled-mode, and even-mode impedances.

Let's codify this into a differential impedance principle:

Coupling between parallel pcb traces decreases their differential (or odd-mode) impedance .

When implementing tightly coupled differential traces on a pcb, one normally reduces the width of the lines within the coupled region in order to compensate for the expected drop in differential impedance.

6.9.2 Why the Odd-Mode Impedance Is Always Less Than the Uncoupled Impedance

The proof relies on the construction of a thing called an equipotential plane midway between two differential traces. Due to symmetry, all the electric fields in the odd-mode situation will lie perpendicular to this plane. Therefore, the potential everywhere along the equipotential plane will be zero. If the potential everywhere along the plane is zero, I could replace the imaginary equipotential plane with a real, solid copper wall and it wouldn't make any difference. The odd-mode characteristic impedance is not affected by the wall. What's really neat about this construction is that once the wall is in place , the problem is partitioned into two noninteracting zones. This gives us a way to evaluate the odd-mode impedance using a single trace and a solid copper wall instead of two traces. If you think about the impact of the wall on the characteristic impedance of a single trace, it's pretty obvious that the wall will add capacitance and decrease the impedance. The net result of this argument is that the odd-mode impedance of a coupled structure is always less than the uncoupled impedance Z .

6.9.3 Differential Reflections

High Speed Digital Design Online Newsletter , Vol 2, Issue 21 John Lehew writes

In the High-Speed Digital Design book and in a few other places it states the fractional reflection G coefficient caused by a mismatch in impedance is

Equation 6.14

 

where	Z is the characteristic impedance of a primary transmission line, and
	Z 2 is the characteristic impedance of a mismatched section to which the primary line is coupled.

This formula is typically used to calculate reflections that happen in a single transmission line that is referenced to a ground plane. Does this formula also apply to differential or balanced lines?

Reply

Thanks for your interest in High-Speed Digital Design .

Aside from the complications introduced by unbalanced modes, differential transmission lines behave pretty much like single-ended ones. Equation [6.14] applies to both.

Assume I have a section of differential transmission line with a differential impedance of Z 1 . Assume I couple that into a load with differential impedance Z 2 (it doesn't matter whether Z 2 is a lumped-element load or another section of differential transmission line with characteristic impedance Z 2 ). The size of the signal that bounces off the joint, in comparison to the size of the incoming signal, is given by your equation for the reflection coefficient G .

Let's do an example using unshielded twisted-pair cabling (UTP). Suppose I couple a section of category 5, 100- W (nominal) UTP cabling to another section of category 4 120- W (nominal) UTP cabling (such cable is available only in France). The reflection off the joint will be of (nominal) size:

Equation 6.15

 

Now, what could go wrong with this simple example? If the cable is inherently un balanced (i.e., more capacitance from one side to ground than on the other), then you have a more complicated situation. In general, there are four modes of propagation involved in the problem, one differential mode and one common mode for each of the two cables. The complete problem is described by a 4x4 coupling matrix whose entries vary with frequency.

Imperfections in the balancing of the cable result in cross-coupling between the differential modes and the common modes at the joint, which is one of the things that creates EMI headaches .

POINT TO REMEMBER

• Aside from the complications introduced by unbalanced modes, differential transmission lines behave pretty much like single-ended ones.