Approximations to the Fourier Transform

The frequency-domain model discussed in this chapter is based on the Fourier transform. The Fourier transform is one of many transformations that establish relations between the time domain and the frequency domain (Figure 4.2). With it, you can turn time-domain functions into frequency-domain functions, and vice versa. The most important aspect of the Fourier transform is that it changes time-domain convolution (difficult to compute) into frequency-domain multiplication (easy to compute).

Figure 4.2. The Fourier transform maps time-domain functions to frequency-domain functions, turning time-domain convolution into frequency-domain multiplication.

Given a signal x ( t ) and the impulse response of a filter h ( t ), you can compute the output y ( t ) by first Fourier-transforming both x and h to the frequency domain. Then, for all possible frequencies w , form the product X ( w ) H ( w ) and transform the resulting frequency-domain function Y ( w ) back to the time domain using an inverse Fourier transform.

The Fourier transform is defined as

Equation 4.1

Equation 4.2

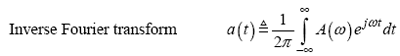
Unfortunately, evaluation of the Fourier transformation requires the calculation of continuous-time integrals, which, unless a closed-form solution is available for your particular signal, is generally impossible to perform. Therefore, a shortcut has been developed for approximating Fourier transformations. The shortcut is called the DFT (discrete Fourier transform).

The DFT is a discrete-time approximation to the Fourier transform. It operates on a vector x n with n 0,1..( N “ 1), translating x n into a discrete-frequency domain according to the following finite sum.

Equation 4.3

Equation 4.4

The DFT [4.3] is closely related to the Fourier transform [4.1] with the exception that both time and frequency have been rendered in a discrete form, changing the continuous integrations of [4.1] into discrete summations. With a suitable mapping between the continuous-time domain and the discrete-time domain, the DFT can successfully approximate the Fourier transform.

The fast-Fourier transform (FFT) is nothing more than a very clever implementation of equation [4.3]. It works only for particular values of N . The most common variety is the Cooley-Tukey FFT, which works only for N equal to a power of two. The FFT algorithm arranges the calculation so that the total effort required to accomplish the sum grows not in proportion to N 2 (as would a simple-minded matrix multiplication) but in proportion to N log 2 N . Its efficacy is so great that the DFT practically never appears in its direct form ”the FFT universally has replaced it. Except for some very subtle differences involving coefficient quantization and sensitivity to rounding errors, the mathematical properties of the FFT and DFT are identical ( [32] , [33] , [34] and [35] ).

NOTE: There is some disagreement in the literature about whether the factor 1/ N in equation [4.3] belongs in the forward DFT, in the inverse DFT, or perhaps split equally as 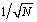in both transformations. If you want the forward and inverse transformations to match so that for any time-domain vector x , you get DFT “1 [ DFT ( x )] = x , then a factor of 1/ N has to go somewhere , but it doesn't really matter where. Here I have shown the factor of 1/ N in the forward transform as implemented in the MathCad function FFT( ). If your tool defines the FFT otherwise , then small adjustments will have to be made in the normalizing constants used with your FFT algorithm (see Section 4.5, "Normalizing the Output of an FFT Routine").

POINTS TO REMEMBER

• The DFT is a discrete-time approximation for the Fourier transform.
• The popular Cooley-Tukey FFT algorithm is a clever, highly efficient implementation of the DFT that works only for N equal to a power of two.