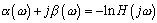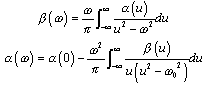Dielectric Effects
Put a piece of bare FR-4 circuit board material (with no copper on either side) into a microwave oven. Bake it on full power for 1 minute. The microwaves noticeably warm the board. Next try a ceramic baking dish. It heats up too (but probably not as much).
In fact, just about any insulating material heats up in a microwave oven. The amount of incident electromagnetic power converted by a dielectric material into heat is called dielectric loss . When an insulating material is used as part of a transmission line, dielectric loss translates into signal attenuation. The higher the dielectric loss, the more attenuation your signals will suffer.
This section describes the dielectric properties of matter, leading to a mathematical definition of the term dielectric loss tangent . In this section I shall restrict the discussion to the types of materials commonly used in high-speed signal transmission applications.
The discussion of dielectric loss begins with a detailed examination of the phase of magnitude of currents flowing in solid materials. Figure 2.27 depicts the measurement of the current through a solid block of material under the influence of an externally applied electric field. [18] Equation [2.68] expresses the magnitude and phase of the current in phasor notation.
[18] If the permittivity of the block is linear then you may express the current in phasor notation. Most insulating materials used in digital applications are extremely linear over the range of typically applied voltages.
Figure 2.27. A small block of material generates currents both in phase and in quadrature to an externally applied electric field.
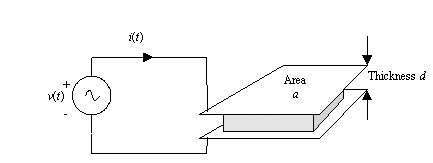
Equation 2.68
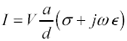
|
where |
V ( w ) is the source voltage as a function of frequency, |
|
I ( w ) is the current as a function of frequency, |
|
|
w is in units of rad/s, |
|
|
a is the surface area of the block held between two thick copper plates (m 2 ), |
|
|
d is the thickness of the block under test (m), |
|
|
s is the conductivity of the material (S/m), and |
|
|
|
In model [2.68] the amplitude of the in-phase current is controlled by parameter s , while the amplitude of the quadrature current is controlled by parameter w  . The amount of in-phase current is called the conduction current . It represents the degree to which the test sample behaves like a resistor. The amount of in-quadrature current is called the displacement current . It represents the degree to which the test sample behaves like a capacitor .
. The amount of in-phase current is called the conduction current . It represents the degree to which the test sample behaves like a resistor. The amount of in-quadrature current is called the displacement current . It represents the degree to which the test sample behaves like a capacitor .
A material is classified as a good conductor if s >> w  , meaning that the conduction current (resistive behavior) is much more significant that the displacement current (capacitive behavior). In a good conductor the current flows mostly in-phase with V. For good conductors, both s and
, meaning that the conduction current (resistive behavior) is much more significant that the displacement current (capacitive behavior). In a good conductor the current flows mostly in-phase with V. For good conductors, both s and  stay fairly constant over a broad range of frequencies, which is what makes [2.68] such a good model for conductors.
stay fairly constant over a broad range of frequencies, which is what makes [2.68] such a good model for conductors.
No matter how terrific a conductor you may have, there is always a critical frequency w c = s /  above which the inexorably growth of w causes w
above which the inexorably growth of w causes w  to vastly exceed s . Beyond the critical frequency the material loses its conductive properties, the displacement current (capacitive behavior) rapidly becomes much more significant than the conduction current (resistive behavior), and the material behaves mostly like a capacitor instead of like a resistor (see box about critical frequency). The material may remain highly conductive above w c , but the capacitive behavior becomes even stronger. Any material operated at a frequency well above w c is classified as a good insulator .
to vastly exceed s . Beyond the critical frequency the material loses its conductive properties, the displacement current (capacitive behavior) rapidly becomes much more significant than the conduction current (resistive behavior), and the material behaves mostly like a capacitor instead of like a resistor (see box about critical frequency). The material may remain highly conductive above w c , but the capacitive behavior becomes even stronger. Any material operated at a frequency well above w c is classified as a good insulator .
In many insulating materials at frequencies well above w c the conduction current, although it remains much smaller than the displacement current, tracks upwards almost in direct proportion to frequency. It tracks in such a way that the ratio s / w  remains almost constant. For these materials it is convenient to express the current in terms of a quadrature term j w
remains almost constant. For these materials it is convenient to express the current in terms of a quadrature term j w  ' , where
' , where  ' stays fairly flat with frequency, and an in-phase term s = w
' stays fairly flat with frequency, and an in-phase term s = w  " , where
" , where  " also stays fairly flat with frequency.
" also stays fairly flat with frequency.
Equation 2.69
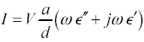
You can rearrange the above equation to emphasize the insulating qualities of a material by lumping both conduction and displacement terms under the umbrella of the j w operator, like this:
Equation 2.70
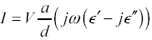
In the form of [2.70] the term  =
=  ' - j
' - j  " is called the complex electric permittivity of a material. The real part
" is called the complex electric permittivity of a material. The real part  ' defines the displacement current, while the imaginary part “
' defines the displacement current, while the imaginary part “  " takes on the role of defining the conduction current. For a good insulator, the imaginary part should be much smaller than the real part.
" takes on the role of defining the conduction current. For a good insulator, the imaginary part should be much smaller than the real part.
For many good insulators the ratio  "/
"/  ' remains so stable across such a wide range of frequencies that it becomes convenient to specify the material properties in terms of the real part
' remains so stable across such a wide range of frequencies that it becomes convenient to specify the material properties in terms of the real part  ' and the ratio
' and the ratio  "/
"/  ' . In this case the ratio
' . In this case the ratio  "/
"/  ' is given the name dielectric loss tangent , or sometimes just the loss tangent . The loss tangent is used to determine the attenuation of a physical transmission line due to dielectric losses.
' is given the name dielectric loss tangent , or sometimes just the loss tangent . The loss tangent is used to determine the attenuation of a physical transmission line due to dielectric losses.
Except for some very unusual quasi-stable situations involved in laser physics, the imaginary part of complex permittivity is always negative, meaning that the value of  " is always positive. The loss tangent is always reported as a positive value.
" is always positive. The loss tangent is always reported as a positive value.
When dealing with the low-permittivity materials commonly used for pcbs and cable insulation, it is convenient to express the permittivity in terms relative to the permittivity of free space.
The permittivity of free space (a perfect vacuum ) is  = 8.854 ·10 “12 . The value of
= 8.854 ·10 “12 . The value of  is entirely real, as free space has no dielectric loss. The permittivity of air differs from
is entirely real, as free space has no dielectric loss. The permittivity of air differs from  by less than one part in 2,000, so for purposes of signal integrity analysis, air and free space are practically the same thing. All other materials have permittivities greater than
by less than one part in 2,000, so for purposes of signal integrity analysis, air and free space are practically the same thing. All other materials have permittivities greater than  and involve some degree of loss.
and involve some degree of loss.
The complex relative permittivity  r of any material may be expressed as the ratio of the complex permittivity
r of any material may be expressed as the ratio of the complex permittivity  to the permittivity of free space
to the permittivity of free space  .
.
Equation 2.71
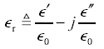
Complex relative permittivity carries with it both real and imaginary parts 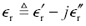 . If you want to refer exclusively to the real part of complex relative permittivity, it is called (in the pcb industry) the dielectric constant . The dielectric constant may be measured for any insulating material as a ratio of capacitances. Specifically , if you construct a capacitor using an insulating material between the plates, and then make a second capacitor with the same physical dimensions but using only a perfect vacuum between the plates, the ratio of the first capacitance to the second equals the dielectric constant of the insulating material. In other words, the dielectric constant is that ratio by which an insulating material enhances, or increases , the effective capacitance of a structure.
. If you want to refer exclusively to the real part of complex relative permittivity, it is called (in the pcb industry) the dielectric constant . The dielectric constant may be measured for any insulating material as a ratio of capacitances. Specifically , if you construct a capacitor using an insulating material between the plates, and then make a second capacitor with the same physical dimensions but using only a perfect vacuum between the plates, the ratio of the first capacitance to the second equals the dielectric constant of the insulating material. In other words, the dielectric constant is that ratio by which an insulating material enhances, or increases , the effective capacitance of a structure.
The dielectric constant of a perfect vacuum is unity, and dry air at standard (sea-level) temperature and pressure is 1.0005. The dielectric constant of all other solid materials is greater than one.
Even if not explicitly stated, the dielectric constant is always defined at one particular frequency. For pcb materials, the usual specification frequencies are 1 KHz, 1 MHz, or 1 GHz. The values at these three frequencies differ , and you must ensure when working with a particular value of dielectric constant that you know the frequency at which your value is specified.
Symbols commonly used for the dielectric constant are k , D k ,  or just plain
or just plain  r . The symbol
r . The symbol  r thus appears somewhat confused as to whether it is a purely real quantity (dielectric constant) or a complex quantity (complex relative permittivity). The rationale behind allowing such confusion is that the imaginary part of relative permittivity is small compared to the real part. When you see
r thus appears somewhat confused as to whether it is a purely real quantity (dielectric constant) or a complex quantity (complex relative permittivity). The rationale behind allowing such confusion is that the imaginary part of relative permittivity is small compared to the real part. When you see  r used as a dielectric constant, you will just have to remember that
r used as a dielectric constant, you will just have to remember that  r carries with it a small, but sometimes important, imaginary component that is being temporarily ignored.
r carries with it a small, but sometimes important, imaginary component that is being temporarily ignored.
The term dielectric constant as used in other industries is sometimes defined as the real part of ordinary (not relative) permittivity and having units of F/m.
Some authors define the term electric susceptibility c e , which is nothing other than the complex relative electric permittivity minus one.
Equation 2.72
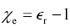
Electric susceptibility is used extensively in the analysis of nonlinear materials. In general it is a function of both frequency and amplitude. Materials used for insulators in transmission-line applications are almost always extremely linear. As a consequence, signal integrity analysts have little use for c e .
POINTS TO REMEMBER
- All insulators exhibit some degree of dielectric loss.
- Make sure you know the frequency at which a value of dielectric constant is specified.
2.12.1 Dielectric Loss Tangent
Dielectric losses in a transmission line scale in proportion to both frequency and length. For any particular construction there exists a certain speed-length product beyond which the material will absorb too much of your signal, leading to system malfunction. The relationship between the dielectric loss specification and the limiting speed-length product is described in the next chapter. This section serves only to explain the way dielectric loss is specified.
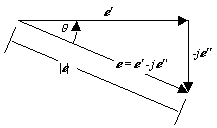
The dielectric loss for materials used to construct pcbs and cables is commonly rated in terms of a dielectric loss tangent, which is the absolute value of the tangent of the phase angle formed by the components of complex permittivity (Figure 2.28):
Figure 2.28. The components of complex permittivity are defined such that  '' is always positive, and the angle q spanned from
'' is always positive, and the angle q spanned from  to
to  ' is also always positive
' is also always positive
Equation 2.73
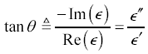
|
where |
tan q is the loss tangent (dimensionless) of a material with complex permittivity |
|
|
The loss tangent precisely equals the dissipation factor , which is a term used in the capacitor industry to specify the quality of capacitors used in power-supply applications. The related term power factor is defined a little differently. Power factor is the ratio of active power to apparent power. In phasor notation it is the ratio VI * / V I , where the asterisk denotes complex conjugation. If the path for current in a circuit is a dielectric material with complex permittivity  , then the power factor equals the ratio
, then the power factor equals the ratio  "/
"/  , which is the sine of the phase angle formed by the components of complex permittivity. For loss tangents less than 10%, the relative difference between dissipation factor and power factor is less than one part in 200.
, which is the sine of the phase angle formed by the components of complex permittivity. For loss tangents less than 10%, the relative difference between dissipation factor and power factor is less than one part in 200.
There is some uncertainty in the literature about whether to call the phase angle of complex permittivity d or q . As a result, the loss tangent has been variously called the tangent of d , tangent of q , or simply tan- d or tan- q . To avoid confusion with the notation for skin depth ( d ), I shall use the term tan- q .
POINTS TO REMEMBER
- Dielectric losses in a transmission line scale in proportion to both frequency and length.
- The dielectric loss tangent is the tangent of the phase angle formed by the real and imaginary components of complex permittivity.
- For small loss tangents, l is approximately the same as the ratio of the imaginary part to the real part of complex permittivity.
2.12.2 Rule of Mixtures
A new dielectric material made by uniform mechanical mixing of two or more constituent materials carries a permittivity  equal to the weighted average, on a volumetric basis, of the permittivities of the constituent materials:
equal to the weighted average, on a volumetric basis, of the permittivities of the constituent materials:
Equation 2.74

|
where |
v n are the volumetric filling factors of the materials involved (assumed to all sum to unity), |
|
|
|
|
|
The form of equation [2.74] applies equally well to relative permittivities (and also to dielectric constants, the dielectric constant being just the real part of relative permittivity).
Equation 2.75
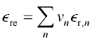
|
where |
v n are the volumetric filling factors of the materials involved (assumed to all sum to unity), |
|
|
|
|
|
Taking only the real parts of [2.75], the same equation works when combining dielectric constants.
Note that definition of [2.74] excludes chemical mixtures for which the electrical properties of the newly created compound may differ vastly from the electrical properties of the constituents. Equation [2.74] only contemplates uniform mechanical mixtures in which the constituents remain chemically intact, but uniformly mixed on a scale smaller than the wavelengths of the signals involved .
As an example, consider the popular FR-4 pcb material. It is made from a mixture of epoxy and glass fibers. The (relative) dielectric constants of epoxy and glass measured at 1 MHz are approximately 3.45 and 5.8 respectively. [19] [21] [22] The glass fibers are on the order of a couple of mils in diameter, which qualifies as quite small compared to signals up to 100 GHz. Equation [2.75] applied to typical epoxy-glass mixtures says the effective dielectric constant 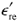 of the mixture should lie somewhere between 3.45 and 5.8.
of the mixture should lie somewhere between 3.45 and 5.8.
[19] TC Edwards [20], p. 73, reports values of 3.8 and 6.3, but doesn't say at what frequency. Brzozowski [21] reports values of 5.8 for e-glass at 1 MHz. Clyde F. Coombs [22] quotes values of 3.45 and 6.2 (p. 31.29), measured presumably at 1 KHz.
Equation 2.76
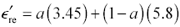
|
where |
a is the relative proportion of epoxy resin, by volume, in the mixture, and |
|
|
Typical values for the resin content by volumetric percentage range from approximately 0.33 to 0.75, resulting in dielectric constants at 1 MHz ranging from a high of 5.0 to a low of 4.0. Beware that resin content is sometimes listed by percentage of weight, which is not the same as percentage of volume.
Equation [2.76] must sometimes be modified to account for the possible presence of air remaining trapped inside the board after lamination. Any residual air must be incorporated into [2.74] as a third constituent with a dielectric constant of unity, occupying part of the total volume. Because air has the lowest possible dielectric constant, the net effect of air in the mixture decreases the dielectric constant of the resulting mixture. Water has an even worse effect because of its large dielectric constant and large loss tangent. Modern vacuum-bag lamination processes in well-controlled manufacturing environments virtually eliminate the possibility of trapped air, though, so air is no longer much of an issue for striplines in high-quality boards .
Air remains a major issue for microstrips, however, because microstrip traces are exposed to (or in close proximity to) air on one side. Although the electric fields between the microstrip and its nearest reference plane remain totally embedded in the dielectric substrate, the electric lines of force spewing up above the trace reside mostly in the air. The effective dielectric constant for the structure must then be a mixture of the dielectric constant of FR-4 and air. The same reasoning applies to twisted-pair cables.
For complicated geometries like microstrips and twisted-pair cables, the constituent dielectrics occupy distinct regions of space, in violation of the uniform-mixing requirement for [2.74]. The spatial distribution of dielectrics is the same at every point along the transmission line (a crucial property), but the dielectrics are not finely mixed. In such a case a new form of the dielectric mixing rule applies with the various dielectric constants weighted not by volume but according to the proportion of the total stored electric field energy contained within each region. These calculations are performed by electromagnetic field simulation software. The net result of field calculations is an effective dielectric constant 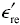 that takes into account the dielectric constants
that takes into account the dielectric constants 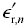 and geometries associated with each of the constituent regions.
and geometries associated with each of the constituent regions.
POINTS TO REMEMBER
- A mixed dielectric carries a permittivity
 equal to the weighted average, on a volumetric basis, of the permittivities of the constituent materials.
equal to the weighted average, on a volumetric basis, of the permittivities of the constituent materials. - Any air or water present in a dielectric mixture will change the dielectric constant of the resulting mixture.
2.12.3 Calculating the Loss Tangent for a Uniform Dielectric Mixture
Suppose you are given a collection of dielectric materials with complex relative permittivities  r,1 ,
r,1 ,  r,2 ...
r,2 ...  r,N , and that the materials are mixed in relative volumetric proportions of a 1 , a 2 ... a N . The loss tangent of the mixture is defined as the ratio of the imaginary part to the real part of the effective complex relative permittivity of the mixture. The effective complex relative permittivity of the mixture may be found using [2.75]:
r,N , and that the materials are mixed in relative volumetric proportions of a 1 , a 2 ... a N . The loss tangent of the mixture is defined as the ratio of the imaginary part to the real part of the effective complex relative permittivity of the mixture. The effective complex relative permittivity of the mixture may be found using [2.75]:
Equation 2.77
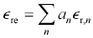
|
where |
a 1 , a 2 ... a N are the relative volumetric proportions of the various materials (all summing to one), |
|
|
|
|
|
Separating equation [2.77] into its real and imaginary parts,
Equation 2.78
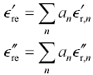
And forming the effective loss tangent ratio,
Equation 2.79

|
where |
tan q e represents the effective loss tangent of the resulting mixture (dimensionless). |
You can simplify equation [2.79] somewhat by substituting 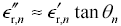 for the imaginary term associated with each constituent.
for the imaginary term associated with each constituent.
Equation 2.80
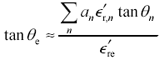
|
where |
a n are the relative volumetric proportions of the constituent materials, |
|
|
|
|
tan q n are the loss tangents of the constituent materials (dimensionless), |
|
|
|
|
|
tan q e represents effective the loss tangent of the resulting mixture (dimensionless). |
The above expression may be used to determine the loss tangent of any uniform mechanical mixture, given that you know the weighting factors a n , and also given that you have identified all the constituents .
As pointed out by Alina Deutsch [11] , "...dielectric loss [in pcbs] is very much dependent on any solvents that get trapped inside the multilayer stack [as well as the] characteristics of the epoxy and fiberglass reinforcing material." Even small percentages of lossy contaminates can easily double the measured loss in a finished product as compared to the calculated loss based on assumed bulk-material parameters. When in doubt, directly measure the dielectric loss on a test board.
In mixtures involving only two constituents, when the second constituent is air, equation [2.80] may be simplified by noting that for air, tan q equals zero. The effective volumetric mixing fraction for the non-air constituent is then called the filling factor q .
Equation 2.81
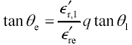
|
where |
q is the filling factor (relative volumetric proportion) of the first material, |
|
|
|
|
tan q 1 is the loss tangent of the non-air constituent material (dimensionless), |
|
|
|
|
|
tan q e is the effective loss tangent of the resulting mixture (dimensionless). |
Equation [2.81] may be used to determine the loss tangent for any mixture of one constituent and air, given that you know the filling factor q . If you don't know q , read the next section.
When working microstrip and embedded microstrip problems associated with FR-4 materials, parameters  and tan q 1 represent the composite properties of a uniform mixture of epoxy resin and glass fibers.
and tan q 1 represent the composite properties of a uniform mixture of epoxy resin and glass fibers.
POINT TO REMEMBER
- The loss tangent for a mixed dielectric can be calculated from the loss tangents and filling factors of the constituent materials.
2.12.4 Calculating the Loss Tangent When You Don't Know q
This section describes a specialized method of determining the effective loss tangent for microstrip and twisted-pair transmission lines.
The design process for these media usually begins with two types of information: first, the dielectric constant  r,1 of the insulating material, and second, the geometric configuration of the conductors, insulating regions, and air-filled regions in the vicinity of the conductors.
r,1 of the insulating material, and second, the geometric configuration of the conductors, insulating regions, and air-filled regions in the vicinity of the conductors.
Given these input parameters, any of a number of software-driven field-solver algorithms can calculate the impedance and propagation velocity of the transmission structure. From the propagation velocity v you can easily determine the effective dielectric constant of the structure:
Equation 2.82
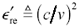
|
where |
c is the velocity of light in vacuum, equal to 2.998 ·10 8 m/s, |
|
v is the propagation velocity of the structure given by your field simulator (m/s), |
|
|
NOTE: |
v equals the inverse of line delay (for delay measured in units of s/m), and |
Provided that you know the loss tangent of the insulting material, you now have in hand three of the four parameters needed to apply [2.81]. The missing piece of information is the filling factor q . Fortunately, you can work backwards from  and
and 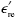 to determine q . Begin by noting that the value of q is defined so that the mixing function [2.75] produces the correct dielectric constant
to determine q . Begin by noting that the value of q is defined so that the mixing function [2.75] produces the correct dielectric constant  re :
re :
Equation 2.83
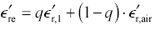
|
where |
|
|
|
|
|
q is the filling factor you wish to find, and |
|
|
|
Solving [2.83] to find q , [20]
[20] Equation [2.84] works provided that k 1 exceed unity. In the rare but theoretically conceivable instance that the insulating material has unit dielectric constant but nonzero loss tangent, the result of equation [2.84] would be undefined.
Equation 2.84
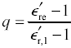
Plugging this value of q into [2.81] yields a very useful expression for tan q e .
Equation 2.85
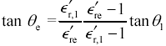
|
where |
|
|
tan q 1 is the loss tangent of the dielectric material used to build the structure, |
|
|
|
|
|
tan q e is the effective loss tangent of the resulting structure. |
POINT TO REMEMBER
- The filling factor for a dielectric-air mixture may be inferred from the velocity of propagation.
2.12.5 Causality and the Network Function Relations
The real and imaginary portions of any realizable network function bear certain subtle yet incontrovertible relations to each other. The original and best description of these relations appears in Network Analysis and Feedback Amplifier Design [12] . Another good reference is The Fourier Integral and Its Applications [13] page 206. A mere shadow of the power and originality of these early descriptions may also be found in more modern texts on the subject of analog filter design.
The rules laid down by Bode declare that you cannot change the magnitude of a network function without also making a corresponding change in the phase. The separate parts, magnitude and phase, are inseparably linked.
Every permittivity function  must abide by the network-function relations (see box Network Function Relations ). These relations become especially important when supplying loss tangent and dielectric constant data to signal integrity simulation programs. Here I am thinking of the H-SPICE W-element model for a lossy transmission line. In some versions the model allows the arbitrary prescription of loss tangent and dielectric constant data as a function of frequency. If the real and imaginary parts of the permittivity so defined do not bear the proper relationships to each other, the implied time-domain waveforms associated with the specified permittivity may be noncausal or nonreal or nonminimum-phase. Any of these conditions will throw SPICE into fits, producing a bogus simulation.
must abide by the network-function relations (see box Network Function Relations ). These relations become especially important when supplying loss tangent and dielectric constant data to signal integrity simulation programs. Here I am thinking of the H-SPICE W-element model for a lossy transmission line. In some versions the model allows the arbitrary prescription of loss tangent and dielectric constant data as a function of frequency. If the real and imaginary parts of the permittivity so defined do not bear the proper relationships to each other, the implied time-domain waveforms associated with the specified permittivity may be noncausal or nonreal or nonminimum-phase. Any of these conditions will throw SPICE into fits, producing a bogus simulation.
The difficulty with crafting a response both causal and real is the extremely subtle interplay of the real and imaginary components of H ( p ). Fortunately, [12] provides considerable guidance about the relationship between the magnitude and phase of any realizable network function. Of special interest are his conclusions regarding the behavior of the magnitude and phase of any real, causal, and minimum-phase network function when drawn on a log-log scale, as a function of the imaginary-axis frequencies j w . Bode proves that in places where the slope on a log-log plot of a network function A ( j w ) is fairly constant over a wide band, the phase of A ( j w ) must equal p /2 times the slope.
In accordance with this familiar result, good capacitors with impedance slopes of “ 20 dB/ decade (that's a slope of “1 on a log-log plot) must always posses a phase angle of precisely - p /2 radians. Good inductors, on the other hand, with impedance slopes of +20 dB/decade (that's a slope of +1 on a log-log plot), always have a phase angle of + p /2 radians.
The general theory of phase/magnitude relations also applies to the case of a dielectric material with a loss tangent that remains constant over a wide range of frequencies. Bode's results say that if the phase of the complex permittivity [21] is “ q over a wide region, then the log-log slope of the magnitude of the permittivity over that region must be very close to “(2/ p ) q . From this simple observation you may conclude that the only way to make a complex relative permittivity function with a constant loss tangent at all frequencies is like this:
[21] According to Figure 2.28 the phase of the permittivity function is negative (- q ).
Equation 2.86
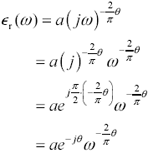
|
where |
|
|
q is the phase angle formed by the components of complex permittivity (rad), and |
|
|
a is an arbitrary real constant. |
Examining the form of [2.86], several objections come to mind. First, the relative permittivity goes to zero at high frequencies. This behavior is not physically permitted, as nothing can have a dielectric constant less than one. Second, the relative permittivity goes to infinity at zero, which implies infinite amounts of capacitance near DC. Neither trait seems physically desirable.
It is important to realize that these objections are not shortcomings of the formulation [2.86]; they are shortcomings of the concept of constant loss tangent. The lesson learned from examining [2.86] is that complex permittivity cannot have a constant loss tangent at all frequencies. The frequency range over which the loss tangent is zero may be very large, but cannot be infinite.
Whether or not the shortcomings of [2.86] cause difficulty depends on the simulation technology you use. If you choose frequency-domain simulation, then [2.86] works fine, because a frequency-domain simulator evaluates  r only over a limited range of frequencies stipulated by the needs of the Fast-Fourier Transform (FFT). As long as
r only over a limited range of frequencies stipulated by the needs of the Fast-Fourier Transform (FFT). As long as  r remains well behaved over the required range, peculiar behavior at infinity or DC doesn't matter.
r remains well behaved over the required range, peculiar behavior at infinity or DC doesn't matter.
For example, in an FFT with one million points the ratio between the highest and lowest frequencies sampled (excluding DC) is 500,000 to 1. That may sound like a huge ratio, but over that range the slope in magnitude induced by [2.84] is so gentle that for a loss tangent of 0.02 (typical for FR-4) less than a 20% variation in the dielectric constant results. No big deal.
A frequency-domain simulator handles DC as a special case (just like SPICE does a separate DC analysis before starting its AC analysis). At DC the limiting value of the admittance j w  r stipulated by [2.84] is zero, so it works just like any other capacitor ”it's an open circuit.
r stipulated by [2.84] is zero, so it works just like any other capacitor ”it's an open circuit.
Equation 2.87
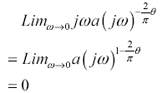
If all you know about a material is its worst-case loss tangent over the frequency range of interest and the dielectric constant at one particular frequency, then for frequency-domain simulation purposes, equation [2.84] functions beautifully. It generates the worst amount of dispersion possible for the transmission line, and it guarantees a real, causal, minimum-phase response.
When using [2.84], set q such that tan( q ) equals the specified loss tangent, and set 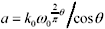 to provide the appropriate value of dielectric constant at reference frequency w . For loss tangents less than 0.05, you may assume q = tan q to within better than one part in 1,000.
to provide the appropriate value of dielectric constant at reference frequency w . For loss tangents less than 0.05, you may assume q = tan q to within better than one part in 1,000.
Given w , k , and q , here are two modified forms of [2.86].
Equation 2.88
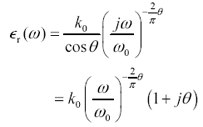
|
where |
|
|
q is the phase angle formed by the components of complex permittivity, and |
|
|
k is the dielectric constant (dimensionless) at frequency w (rad/s). |
If you are doing SPICE simulation (using the W-element model or any other model that accepts a table of frequency-varying values for dielectric constant and loss tangent), then you may not have precise control over the frequencies at which SPICE attempts to perform its analysis. You may in this case want to produce a table of complex permittivity values that has constant loss-tangent in a given frequency band but does not tend towards infinity as w 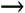 0.
0.
A reasonable solution to the problem of infinities is to feather the phase linearly to zero below some critical frequency w 1 . Provided that w 1 falls well below the lowest frequency of interest in your simulations, the feathering will have little or no effect on the actual time-domain results, but will eliminate the infinite amplitude values at DC.
Here is a magnificent permittivity function with constant phase q 1 above frequency w 1 , but with the phase feathered linearly to zero below w 1 . The magnitude and phase are matched to produce a real, causal, minimum-phase result (Figure 2.29). The function a is developed through meticulous application of the integral equations associated with the network relations in [12] and [13] .
Equation 2.89
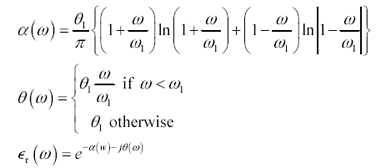
|
where |
|
|
a is the log attenuation ( negative of the log-magnitude) of |
|
|
q is the angle formed by the components of |
|
|
w is the frequency of operation (rad/s), and |
|
|
q 1 is the limiting value of phase above w 1 (rad/s). |
Figure 2.29. Feathering the phase to zero below w 1 prevents the log attenuation from going to infinity at DC, but leaves the remainder of the curve unchanged. ( q 1 = 0.02, w 1 = 10 9 rad/s).

Many other models for complex permittivity can be used. As long as the dielectric constant and loss tangent from the model match your material properties over the frequency range of interest, and the model scales in a causal, minimum-phase fashion across all frequencies, it should work. Of particular interest is one model proposed by Svensson and Dermer [14] involving a continuous array of poles located on the real axis. Other authors have used a finite array of poles located on the real axis, with the positions and weights adjusted by optimizing procedure to best match measured parameters.
POINT TO REMEMBER
- The real and imaginary portions of any realizable network function bear certain subtle yet incontrovertible relations to each other. Specifying one without the other leads to non-realizeable circuit results.
2.12.6 Finding  r to Match a Measured Loss Tangent
r to Match a Measured Loss Tangent
Although measured values for loss tangent can be quite accurate, measured values for the dielectric constant are notoriously inaccurate . The accuracy of the loss tangent measurement flows from its definition as the ratio of two currents in quadrature, both defined at the same frequency. Various precautions may be taken during measurement to ensure the accuracy of the measured results.
Dielectric constant measurements, on the other hand, are taken over vastly differing frequencies, leading to certain natural inaccuracies in the calibration of the test setup.
Suppose, then, that you have access to loss tangent data for which no dependable dielectric constant data are available. In this case you must synthesize a magnitude function to match the specified phase information, matching in the sense of being real, causal, and minimum-phase. Attempts to do so using the network relations in their integral-equation form may prove unsatisfactory due to the obvious divide-by-zero problems inherent in those equations. In the world of abstract mathematics, skilled mathematicians can overcome these divide-by-zero errors with suitable limiting arguments, but in the world of practical, everyday engineering calculations your typical math-processing spreadsheet programs just can't do those sorts of integrals.
To get you past the integral-equation difficulties, I shall describe an FFT technique for computing Hilbert-transform pairs. This technique generates a matching magnitude function for any arbitrary phase function. The disadvantage of this technique is that in order to ensure accuracy of the finished result, it requires a lot of points in the FFT.
Begin by deciding the range of frequencies over which the magnitude must be synthesized . This range spans from some low value f 1 , below which the circuit reacts essentially at DC, to some high value f 2 corresponding to the bandwidth of the digital signals involved. A digital transmission line with propagation delay t p mandates f 1 no greater than 1/(2 p t p ). Signal rise/fall times of t r require f 2 no less than 1/(2 t r ). For the method to work successfully, the FFT must sample at a frequency at least 20 times higher than f 2 and contain a number of points N at least equal to 400 f 2 /f 1 .
The oversampling ratio in the FFT sampling frequency is the factor by which the FFT sampling frequency f s exceeds the bandwidth f 2 of the digital signals in your simulation. In this application the oversampling ratio controls the degree of distortion in the upper band edge of the finished permittivity function. This distortion is introduced by the Hanning window, which is included to suppress Gibb's phenomena in the time-domain response. An oversampling ratio of 20:1 produces distortion at f 2 of roughly 1% of the log magnitude of the permittivity. The upper band-edge distortion changes approximately in inverse proportion to the oversampling ratio.
The number of points in the FFT controls the spacing of the frequency-sampling grid used to represent the permittivity function. The frequency-sampling spacing is f s / N . In the low-frequency zone near f 1 you should use a spacing no greater than f 1 /20, which implies a lower bound on N .
Equation 2.90
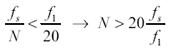
Substitute 20 f 2 for f s ( assuming you followed my advice on f s ),
Equation 2.91

Now substitute the expressions for f 1 and f 2 to get the final form:
Equation 2.92
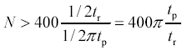
According to [2.92], the number of points N used in your FFT operations must exceed 400 p times the number of rise times stored in the transmission line at any given instant. The value of N is usually selected to be the next highest power of two above the bound set by [2.92].
Once you have selected an appropriate N , define indexes for the FFT operations:
Equation 2.93
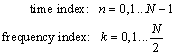
Evaluate the loss tangent on a dense grid of frequencies, and fill in values for the phase of the permittivity.
Equation 2.94
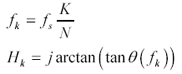
Notice here that I have defined H only for positive frequencies in accordance with the way real-valued FFT routines usually operate . The frequency-domain parameters are specified as a vector of complex values using the frequency-domain index k, while the time-domain values are specified as a vector of real values using the time-domain index n .
Next you must window the function H to bring the imaginary part of the response down to zero at frequency sample point N /2. If you don't apply the window, then Gibb's phenomenon will induce horrible-looking wiggles in the implied time-domain response. I've chosen the Hanning window in this case as a reasonable compromise between the accuracy of the frequency-domain results below f 2 and the suppression of Gibb's phenomenon in the time-domain response.
Equation 2.95
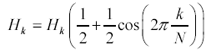
Apply the inverse FFT to vector H , producing a real-valued time-domain response vector h of length N .
Equation 2.96
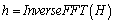
At this point I must diverge to discuss briefly some of the properties of the Fourier transform. Any time-domain function may be broken into its odd and even constituents h = h e + h , where h o is a strictly odd function [22] and h e is strictly even. The odd part h o controls the imaginary part of the frequency response, while the even part h e controls the real part of the frequency response. In the case at hand, h o controls the phase of the permittivity, while h e controls the log magnitude.
[22] In continuous time, an odd function satisfies h ( t ) = “ h ( “ t ). In discrete time, the relation is h k = “ h N-k .
As computed, h is already strictly odd, as befits its origin from a purely imaginary frequency specification. To the function h you can therefore add any strictly even function h e without distorting the phase of the permittivity.
Your task is to find a purely even function h e such that the time-domain response h + h e becomes zero for all negative times. In mathematical terms,
Equation 2.97
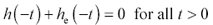
Substituting the definitions of odd and even functions for negative times produces a new equation:
Equation 2.98
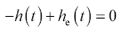
Adding 2 h to both sides,
Equation 2.99

Equation [2.99] demonstrates that when the function h e is chosen to null the time-domain response for all negative times, then for all positive times the function h + h e simply equals 2 h . I know this sounds too easy, but that's how you find the time-domain response associated with the logarithm (log magnitude and phase) of the frequency-response of the permittivity. So, the next step is to create a new vector g which zeroes h for all negative times and doubles it for all positive times.
Equation 2.100
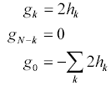
Next transform g from the time to the frequency domain, producing a complex-valued vector of length 1 + ( N /2)
Equation 2.101
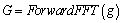
Vector G represents the magnitude (nepers) and phase (radians) of a real-valued, causal, and minimum-phase permittivity response. Values for dielectric constant and loss tangent may be extracted from G.
Equation 2.102
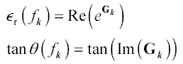
Figure 2.30 illustrates the results obtainable with the FFT method. In this example the input phase is taken directly from [2.89] with parameters tan q = 0.02 and w 1 = 10 9 rad/s. The desired phase curve is marked on the figure as "design-goal q ( w )." For this particular phase specification, [2.89] stipulates the correct log-attenuation curve, marked in the figure as "design-goal a ( w )."
Figure 2.30. The FFT method synthesizes a log-attenuation curve to closely match any given phase curve ( q 1 = 0.02, w 1 = 10 9 rad/s).
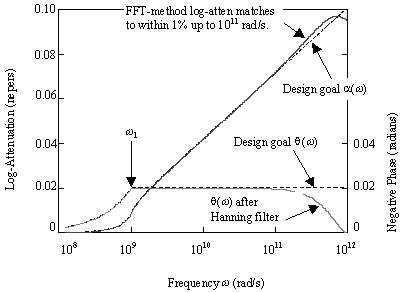
The problem parameters are to synthesize a good phase-and-magnitude pair for all frequencies up to 10 11 rad/s (15.9 GHz), using only the input phase curve and the FFT method. For this purpose, the FFT sample frequency is chosen as 2 ·10 12 rad/s (318 GHz). The FFT has 65,536 points, which establishes a sampling-frequency grid spacing of 30.5 ·10 6 rad/s = 4.80 MHz. Such parameters are appropriate for a 6-inch trace carrying 10 Gb/s with rise/fall times of 30 ps.
The FFT procedure windows the phase curve as shown, and then produces a matching log-attenuation curve marked as the "FFT-method log-atten." In the band from DC to 10 11 rad/s the FFT-method log-attenuation curve matches the design goal to within 1%. The FFT-method log-attenuation curve and the FFT-method windowed phase curve must be used together; do not mix and match the design goal components with the FFT-method components.
In [2.100] I have taken the liberty of adjusting g to guarantee that g has zero DC content. This sets the real part of G to zero, which in turn ensures that the DC value of e r equals unity. After computing the FFT, you may then scale the dielectric constant without changing the loss tangent. Choose a constant A such that A  r ( f ) gives you the particular dielectric constant you need at one particular frequency f and thereafter use A
r ( f ) gives you the particular dielectric constant you need at one particular frequency f and thereafter use A  r ( f k ) and tan q ( f k ).
r ( f k ) and tan q ( f k ).
To evaluate  r and tan q at frequencies not on the dense grid established by the FFT, use linear interpolation.
r and tan q at frequencies not on the dense grid established by the FFT, use linear interpolation.
In the event you do not have accurate loss tangent data extending down to DC, use what data you have, filling in all unknown values down to frequency f 1 with a constant loss tangent, and below that feathering the loss tangent linearly to zero at DC.
POINT TO REMEMBER
- You can calculate a variation in dielectric constant to match any specified loss tangent.
2.12.7 Kramers-Kronig Relations
The Kramers-Kronig relations (see [5] page 83, and [15] ) are of the same ilk as the network function relations in the previous section. They are a specialized form of those relations, crafted specifically to express the relation between the real and imaginary parts of complex permittivity ( 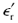 and
and 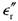 respectively).
respectively).
Equation 2.103
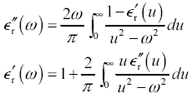
If you are familiar with the standard relations for the real and imaginary parts of a causal network function (see [12] and [13] page 200), you may recognize some differences here from the normal presentation. In particular, the integrand of the first equation here operates on the quantity 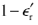 instead of
instead of 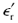 , a trivial modification that does not mathematically affect the outcome of the integral, but does improve the computational stability of the integration, the point being that at extremely high frequencies the term
, a trivial modification that does not mathematically affect the outcome of the integral, but does improve the computational stability of the integration, the point being that at extremely high frequencies the term 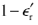 tends toward zero. Another difference is that here
tends toward zero. Another difference is that here 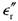 by definition equals the negative of the imaginary part of complex permittivity. A third difference is that here both integrations have been folded around zero.
by definition equals the negative of the imaginary part of complex permittivity. A third difference is that here both integrations have been folded around zero.
POINT TO REMEMBER
- The Kramers-Kronig relations constrain the behavior of the real and imaginary parts of complex permittivity.
2.12.8 Complex Magnetic Permeability
In the science of magnetic materials there exist concepts analogous to complex permittivity; however, since digital applications work for the most part with nonmagnetic materials, we shall not explore that territory. Most conductors (except iron, steel , and nickel) and most insulating materials used in digital applications have a relative magnetic permeability of 1.000 + j 0.000.
Fundamentals
- Impedance of Linear, Time-Invariant, Lumped-Element Circuits
- Power Ratios
- Rules of Scaling
- The Concept of Resonance
- Extra for Experts: Maximal Linear System Response to a Digital Input
Transmission Line Parameters
- Transmission Line Parameters
- Telegraphers Equations
- Derivation of Telegraphers Equations
- Ideal Transmission Line
- DC Resistance
- DC Conductance
- Skin Effect
- Skin-Effect Inductance
- Modeling Internal Impedance
- Concentric-Ring Skin-Effect Model
- Proximity Effect
- Surface Roughness
- Dielectric Effects
- Impedance in Series with the Return Path
- Slow-Wave Mode On-Chip
Performance Regions
- Performance Regions
- Signal Propagation Model
- Hierarchy of Regions
- Necessary Mathematics: Input Impedance and Transfer Function
- Lumped-Element Region
- RC Region
- LC Region (Constant-Loss Region)
- Skin-Effect Region
- Dielectric Loss Region
- Waveguide Dispersion Region
- Summary of Breakpoints Between Regions
- Equivalence Principle for Transmission Media
- Scaling Copper Transmission Media
- Scaling Multimode Fiber-Optic Cables
- Linear Equalization: Long Backplane Trace Example
- Adaptive Equalization: Accelerant Networks Transceiver
Frequency-Domain Modeling
- Frequency-Domain Modeling
- Going Nonlinear
- Approximations to the Fourier Transform
- Discrete Time Mapping
- Other Limitations of the FFT
- Normalizing the Output of an FFT Routine
- Useful Fourier Transform-Pairs
- Effect of Inadequate Sampling Rate
- Implementation of Frequency-Domain Simulation
- Embellishments
- Checking the Output of Your FFT Routine
Pcb (printed-circuit board) Traces
- Pcb (printed-circuit board) Traces
- Pcb Signal Propagation
- Limits to Attainable Distance
- Pcb Noise and Interference
- Pcb Connectors
- Modeling Vias
- The Future of On-Chip Interconnections
Differential Signaling
- Differential Signaling
- Single-Ended Circuits
- Two-Wire Circuits
- Differential Signaling
- Differential and Common-Mode Voltages and Currents
- Differential and Common-Mode Velocity
- Common-Mode Balance
- Common-Mode Range
- Differential to Common-Mode Conversion
- Differential Impedance
- Pcb Configurations
- Pcb Applications
- Intercabinet Applications
- LVDS Signaling
Generic Building-Cabling Standards
- Generic Building-Cabling Standards
- Generic Cabling Architecture
- SNR Budgeting
- Glossary of Cabling Terms
- Preferred Cable Combinations
- FAQ: Building-Cabling Practices
- Crossover Wiring
- Plenum-Rated Cables
- Laying Cables in an Uncooled Attic Space
- FAQ: Older Cable Types
100-Ohm Balanced Twisted-Pair Cabling
- 100-Ohm Balanced Twisted-Pair Cabling
- UTP Signal Propagation
- UTP Transmission Example: 10BASE-T
- UTP Noise and Interference
- UTP Connectors
- Issues with Screening
- Category-3 UTP at Elevated Temperature
150-Ohm STP-A Cabling
- 150-Ohm STP-A Cabling
- 150- W STP-A Signal Propagation
- 150- W STP-A Noise and Interference
- 150- W STP-A: Skew
- 150- W STP-A: Radiation and Safety
- 150- W STP-A: Comparison with UTP
- 150- W STP-A Connectors
Coaxial Cabling
- Coaxial Cabling
- Coaxial Signal Propagation
- Coaxial Cable Noise and Interference
- Coaxial Cable Connectors
Fiber-Optic Cabling
- Fiber-Optic Cabling
- Making Glass Fiber
- Finished Core Specifications
- Cabling the Fiber
- Wavelengths of Operation
- Multimode Glass Fiber-Optic Cabling
- Single-Mode Fiber-Optic Cabling
Clock Distribution
- Clock Distribution
- Extra Fries, Please
- Arithmetic of Clock Skew
- Clock Repeaters
- Stripline vs. Microstrip Delay
- Importance of Terminating Clock Lines
- Effect of Clock Receiver Thresholds
- Effect of Split Termination
- Intentional Delay Adjustments
- Driving Multiple Loads with Source Termination
- Daisy-Chain Clock Distribution
- The Jitters
- Power Supply Filtering for Clock Sources, Repeaters, and PLL Circuits
- Intentional Clock Modulation
- Reduced-Voltage Signaling
- Controlling Crosstalk on Clock Lines
- Reducing Emissions
Time-Domain Simulation Tools and Methods
- Ringing in a New Era
- Signal Integrity Simulation Process
- The Underlying Simulation Engine
- IBIS (I/O Buffer Information Specification)
- IBIS: History and Future Direction
- IBIS: Issues with Interpolation
- IBIS: Issues with SSO Noise
- Nature of EMC Work
- Power and Ground Resonance
Points to Remember
Appendix A. Building a Signal Integrity Department
Appendix B. Calculation of Loss Slope
Appendix C. Two-Port Analysis
- Appendix C. Two-Port Analysis
- Simple Cases Involving Transmission Lines
- Fully Configured Transmission Line
- Complicated Configurations
Appendix D. Accuracy of Pi Model
Appendix E. erf( )
Notes
EAN: N/A
Pages: 163
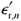 are the dielectric constants of the constituent materials, (dimensionless),
are the dielectric constants of the constituent materials, (dimensionless), is the effective dielectric constant of the resulting mixture (dimensionless), and
is the effective dielectric constant of the resulting mixture (dimensionless), and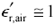 represents the dielectric constant of air.
represents the dielectric constant of air.