Pcb Noise and Interference
There are two major sources of noise and interference in a high-speed pcb communications channel: reflections and crosstalk.
Radio-frequency interference rarely afflicts digital logic signals in a direct way if the system is reasonably well shielded , the traces are kept close to a solid reference plane, and the digital logic levels are reasonably large (1 volt or more).
5.3.1 Pcb: Reflections
When you blast a high-speed step edge into a reasonably well- terminated pcb trace, most of your signal power reaches the far end at the same time, duplicating the size and shape of the original transmitted waveform. The received signal may be distorted or reduced in amplitude, but in a good system most of the signal power at least arrives reasonably coincident in time.
Any portions of the original transmitted signal that bounce off imperfections with the transmission structure, arriving later at the far-end load, are called far-end reflections . If the reflections arrive at the far end during the current baud period, they are considered a form of settling problem. Echoes that arrive during the reception of some later baud constitute a source of random noise to the receiver at the far end of the cable. In either case, the peak amplitude of the reflections must be limited to a value compatible with the noise margin budget of your logic family. The following sections detail a number of transmission-line imperfections that can generate substantial reflections.
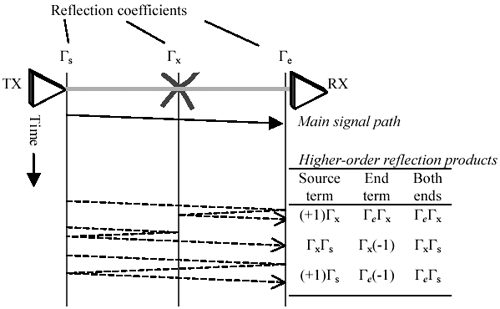
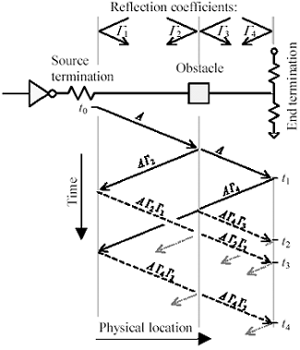
Pcb traces terminated at both ends enjoy a great advantage in immunity to reflections as compared to their singly terminated cousins (either the end-terminated or source-terminated variety). Figure 5.13 illustrates this point with a simplified time-space reflection diagram estimating the magnitude of all second-order reflections reaching the far end of a generic serial link. This figure assumes that an imperfection in the transmission structure at point x creates a small reflection of magnitude G x . In a source-terminated structure the magnitude of the reflection coefficient G e is near unity, so the end-products G e G x and G e G s will be roughly the same size as G x and G s respectively. Similarly, the magnitude of the reflection coefficient G s in the end-terminated structure is near unity (the driver has to have a low impedance or else the transmitted waveform wouldn't be full sized ), so in that case the products G x G s and G e G s will be roughly the same size as G x and G e respectively. The both-ends-terminated structure provides a good attenuation of the reflected signal at both ends of the transmission line, substantially attenuating all second-order reflection products. To first order, therefore, the reflection at G x has little effect on signal quality in a both-ends-terminated structure.
Figure 5.13. Second-order reflection products for a serial link are greatly attenuated by the use of both-ends termination.
The relative immunity to reflections enjoyed by both-ends-terminated structures extends to reflections generated due to poor terminations, vias, connectors, or any other type of impedance mismatch.
5.3.1.1 Both Ends Termination
POINT TO REMEMBER
- Pcb traces terminated at both ends enjoy a great advantage in immunity to reflections as compared to their singly terminated cousins.
5.3.1.2 Pcb: Lumped-Element Reflections
A shunt capacitance connected in the middle of an otherwise long, uniform transmission structure will distort any signal that passes by. In response to an incoming step edge the distortion takes two specific formsa backwards -propagating reflection and an impairment of the forward-propagating signal.
The reflected signal is a brief pulse with a polarity opposite the polarity of the incoming step. The polarity is opposite because a capacitor, when interacting with a fast-moving step edge, draws at first a large surge of current. The surge of current required to charge the capacitor has the same effect as the temporary connection of a low-impedance shunt across the transmission line; namely, it creates an inverted reflection. In the steady-state condition after the traveling pulse has passed, the reflection effect ceases because capacitors have no effect on an unchanging signal. For small reflections, the duration of the reflected pulse approximately equals the rise or fall time t r of the incoming step edge.
The peak amplitude a of the reflected pulse is given approximately by
Equation 5.15
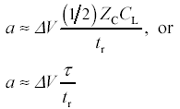
|
where |
a is the peak magnitude of the reflected signal, volts , |
|
D V is the amplitude of the incoming step, volts, |
|
|
t is a time constant computed from the lumped-element capacitance C L and the transmission-line impedance Z C , having the value t = Z C C L /2, |
|
|
and |
|
|
t r is the 10% to 90% risetime of the incoming step, in seconds. |
Equation [5.15] derives from the Fourier transform expression for the reflection coefficient G ( w ) = - j w t /(1+ j w t ) that occurs when a signal traveling in a line of impedance Z C encouters a load formed by the lumped-element capacitor C L in parallel with another section of transmission line having impedance Z C . Equation [5.15] assumes that the time constant t is small compared to t r , so that the term j w t in the denominator of the reflection expression may be ignored at all frequencies within the bandwidth of the incoming waveform, leaving the denominator equal to approximately unity. It further assumes that the maximum value of the derivative of the incoming step approximately equals D V / t r .
Figure 5.15 compares approximation [5.15] to the signal magnitude computed from time-domain simulations. This figure assumes the delay of the transmission line segments on either side of the lumped-element load each exceed t r /2. Under that condition, the fully developed reflection amplitudes listed in Figure 5.15 apply. The same fully developed reflection amplitude applies if either side of the lumped-element load is well-terminated (e.g., if the lumped load is located coincident with an end termination).
Figure 5.15. For reflections less than 25%, the simple approximation [5.12] works remarkably well.
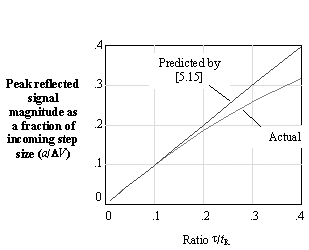
For small reflections less than 25%, the simple approximation predicts the reflected signal amplitude remarkably well. Any time the simple approximation indicates a reflection larger than 25%, you should conclude that your system probably won't work. At that point it hardly matters the extent of the accuracy of the simple approximation.
If the length of the transmission segment leading up to the load falls short of t r /2, then the source begins to interact with the lumped-element load directly. This interaction happens before the conclusion of the initial rising or falling edge from the source, with the result that the transmission impairments are either exaggerated or ameliorated, depending upon whether the impedance of the source is greater or less, respectively, than the line impedance.
The magnitude of the reflected pulse subtracts from the magnitude of the forward-propagating signal. The forward-propagating signal therefore does not immediately rise to a full amplitude; instead, it displays a somewhat degraded risetime. The rise or fall time t FWD of the forward-propagating signal is estimated as
Equation 5.16
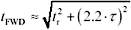
|
where |
t is a time constant computed from the lumped-element capacitance C and the transmission-line impedance Z C , having a value t = Z C C L /2, and |
|
t r is the 10% to 90% risetime of the incoming step, in seconds. |
Provided that the peak magnitude of the reflected signal is no larger than 25% of the incoming step height, the correspondence between [5.16] and actual results computed for a Gaussian input step is better than 1 part in 40.
The group delay of the low-pass filter created by the lumped-element load represents the delay of the signal at approximately the mid-level and is the value that must be added to your propagation-delay calculations. The group delay created by a shunt capacitance in the middle of an otherwise long, uniform transmission structure equals t .
The above approximations may be used to estimate the magnitude of the disturbance caused by any lumped capacitive load, including the parasitic capacitances associated with gate inputs, connectors, through-hole mounting vias, and surface-mount pads.
The same general discussion applies to any series inductance L S with the provision that the time constant t equals L S /(2 Z C ) and the polarity of the reflected signal is positive.
POINTS TO REMEMBER
- A small lumped-element capacitance shunting a transmission line creates a backwards-propagating reflection.
- A small lumped-element inductance in series with a transmission line does the same, but with the opposite polarity.
5.3.1.3 Potholes
POINT TO REMEMBER
- Adjustments to transmission-line width can partially compensate for one small, isolated capacitive load.
5.3.1.4 Inductive Potholes
An inductive pothole (i.e., a connector or via with too much inductance) embedded in the middle of an otherwise long, uniform transmission structure creates a positive reflection. The compensation for this sort of imperfection follows from the same theory given in the article "Potholes," but with slightly different formulas.
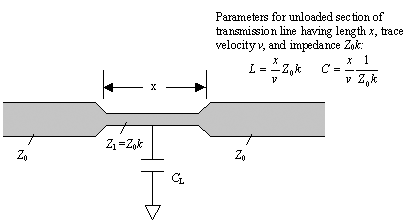
Given a fixed value of k < 1 corresponding to the fattest transmission line you can reliably produce, select the length of the adjusted segment ( x ) so that the ratio of overall inductance and capacitance in the adjusted segment, including the effect of the lumped load, produces an effective impedance of Z . The impedance condition for a series-connected lumped inductor L S is
Equation 5.20
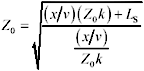
|
where |
Z is the impedance of the surrounding transmission medium, W , |
|
v is the unloaded trace velocity of the adjusted segment, m/s, |
|
|
k = Z 1 / Z defines the unloaded impedance of the adjusted segment, |
|
|
( x / v )( Z k ) is the unloaded inductance of the adjusted segment, H, |
|
|
( x / v )/( Z k ) is the total capacitance of the adjusted segment, F, and |
|
|
L S represents the series inductance, H. |
Solving for the adjusted trace length x tells you how long (in meters) to make the fat segment for a best compensating match. You may notice in this next formula that the fatter you make the adjusted trace (the smaller the Z 1 and thus the smaller the k ), the shorter you can make the adjusted segment:
Equation 5.21
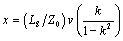
The fat-trace compensation technique works only when the rise or fall time of the incoming edge is significantly slower (three to six times slower) than the effective delay of the adjusted segment. The effective delay t LOADED of the adjusted structure (including load) is
Equation 5.22
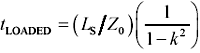
POINT TO REMEMBER
- Adjustments to transmission-line width can partially compensate for one small, isolated series inductance.
5.3.1.5 Who's Afraid of the Big, Bad Bend?
Article first published in EDN Magazine , May 11, 2000Right-angle bends in pc-board traces perform perfectly well in digital designs in speeds as fast as 2 Gbps. In most digital designs, the right-angle bend is electrically smaller than a rising edge. For example, the delay through a right-angle bend in an 8-mil wide, 50- W microstrip trace in FR-4 is on the order of 1 psec. That's less than 1% of a 100-psec risetime. For any object of this tiny physical scale, a lumped-element model should suffice. Years ago, Terry Edwards reproduced in his book [38] (also see [39] ) a good lumped-element model for a right-angle bend. His model indicates that a right-angle bend has two primary effects: a slight delay plus some excess lumped capacitance. You might imagine that as a signal traverses a right-angle corner, the trace appears to grow wider at the corner. This simple idea explains why you see an excess capacitance (lower impedance) near the corner. For an 8-mil wide, 50- W microstrip transmission line in FR-4, the excess lumped capacitance works out to 0.012 pF. Assuming that you are using 100-psec rise and fall times, the size of the reflected signal that bounces off this capacitive discontinuity is 0.30% (that's 0.003) of the incoming step amplitude. I conclude from this analysis that the reflection from a single corner is too small to worry about. (The reflected signal size scales in proportion to the trace width and inversely with rise and fall times.) Some people worry that conduction electrons are traveling so fast that they won't be able to make it around a square corner. Perhaps they might reflect back or fly off into space. Such arguments are ridiculous. Sure, individual electrons move at high speeds, but their aggregate drift velocity is less than 2.5 cm/s (1 in./s) as they bounce from atom to atom. Your average electron smacks into something and changes directions billions of times in a length of 10 mils. Electrons don't have any trouble banging around a corner. Might the electric-field concentration at a sharp, pointy corner create a lot of radiation? Hogwash. As a trace rounds a corner, it stays a constant distance from the underlying reference plane the whole way. The electric field intensity from trace to plane doesn't radically vary at any point along this track except for a modest perturbation in the vicinity of the actual pointy tip of the corner. It's true that a microscopic electric-field probe directly adjacent to the corner would detect this field concentration. However, measurements taken from farther away aggregate radiation from the whole trace, not just the corner. The corner, because it is so small, cannot noticeably affect the far-field radiation. Layout professionals often point out that modern layout systems already round off all the outside corners, assuming that this rounding eliminates the square-corner effect. It doesn't. Rounding the corners removes 21% of the copper in the corner. Edwards shows that you must remove 70% to 90% of the copper from a right-angle bend to neutralize (to first order) the excess capacitance. Rounding removes only a small fraction of the required amount of copper. Rounded-corner right-angle bends work well in digital designs not because they are rounded, but because the corners are too tiny to cause significant problems in the first place. Today, only microwave designers need to worry about right-angle bends. At microwave speeds, roughly 10 times the rate of most digital designs, parasitic capacitance presents 10 times more of a problem. Additionally, microwave designers often use big, fat, 100-mil traces to reduce skin-effect losses, so their corners appear electrically 10 times bigger. Lastly, they also tend to linearly cascade multiple stages. Cascading sums the imperfections in each stage, making microwave designs about 10 times more sensitive to tiny imperfections. Overall, contemporary microwave designs can be 1,000 times more sensitive to right-angle bends than are digital designs. As digital designs push toward higher speeds, you may eventually reach a point where the right-angle bends begin to matter. For example, corners are just beginning to affect the design of 10-Gbps serial connections, and they also contribute perceptibly to skew in certain poorly routed differential pairs. If you accumulate oodles of corners, as in a serpentine delay structure, you may begin to see a little extra delay. Other than these extreme applications, right-angle bends remain electrically transparent. Microwave designs are far more sensitive to right-angle bends than digital designs. Some manufacturing engineers complain about the use of right-angle bends when using wave-soldering equipment. They worry that wayward solder balls or solder flux will get trapped in the inside corners. With reflow soldering and good soldermasking, neither should be a problem. I have heard no other credible negative comments about the manufacturability of right-angle bends, but I am always happy to hear from others whose experience may differ . |
POINT TO REMEMBER
- Right-angle bends in pc-board traces perform perfectly well in digital designs in speeds as fast as 2 Gbps.
5.3.1.6 Stubs and Vias
High Speed Digital Design Online Newsletter , Vol 2, Issue 25Gary Griffin writes I would like to know the effects of short pcb trace stubs and pcb vias, and how to eliminate or reduce them. The stubs could be short traces needed to hook a bus up to a socket, or something like that. Vias are a necessary evil, but how can they be made more transparent to the high-speed signal? The speeds I am talking about range from 400MHz to 3GHz (digital and analog). Reply Thanks for your interest in High-Speed Digital Design . Regarding socket stubs, there isn't much you can do except to not have them (i.e., don't use sockets). I know that's impractical in many cases. About vias,
|
POINT TO REMEMBER
- Blind or buried vias are smaller and have less effect than full-sized vias.
5.3.1.7 Parasitic Pads
Article first published in EDN Magazine , August 17, 2000I'm designing a 2.5-Gbps, OC-48 transceiver card. Between two chips on my board I have several discrete capacitors and resistors to slow the edges and pad the signal. It seems that the very short 2.5-cm (1-in.) trace that I'm using is covered more with part pads than with 50- W trace. My software calculates the [trace] impedance but does not consider these parts . What effect does the pad size have on my trace impedance, and can I neglect it? Code Cubitt The component pads have a big impact on trace impedance, and at 2.5 Gbps, you will really notice it. The basic effect is that each pad contributes a little extra parasitic capacitance C to the trace. A single 1206 pad contributes about 0.72 pF, estimated at 31 pF/cm 2 for a 0.0127-cm thickness of FR-4, (200 pF/in. 2 for a 0.005-in. thickness of FR-4), ignoring fringing fields at the edges. If you space the pads equally along the line, and if the spacing is a small fraction of the signal rise and fall time, then the parasitic capacitance of the pads merely reduces the line impedance. A general rule for the line impedance Z is Equation 5.23
Adding parasitic capacitance increases C . According to the formula, when you increase C , you decrease Z . By whatever ratio you increase the apparent capacitance of the trace, by the square root of that ratio you reduce the effective loaded impedance of the structure. Capacitive loading decreases the effective trace impedance. The exact amount of reduction in the apparent impedance of a loaded trace is proportional to the square root of the ratio of how much capacitance would have been distributed along a raw, unloaded transmission line of the same dimensions, divided by how much capacitance you end up with after you add the equally spaced loads. A good formula for the total capacitance C LINE , distributed along an unloaded transmission line, is Equation 5.24
If the total load capacitance added to the trace is C LOAD , you can write the impedance-reduction-ratio formula as Equation 5.25
If the loads are equally spaced, at least you still have a transmission line with a defined (albeit rather low) impedance. You might consider shrinking the line width to get the impedance back up to your target value of Z .
If the loads are not equally spaced or if their spacing is too great, the signal bounces back and forth between the various capacitive discontinuities in a disagreeable manner. The worst reflection coefficient G that you can get from an isolated capacitive discontinuity in the middle of an otherwise perfect transmission line is Equation 5.26
If one section of your line has many loads, you should decrease the line width in that section to compensate but leave the line width at its normal size over the long unloaded sections. Remember that loads sufficiently heavy to decrease the line impedance also increase the line delay. By whatever ratio the loads reduce the trace impedance, they increase the trace delay. The best way to reduce the effect of parasitic loading is to use smaller parts. The smaller the parts, the better (for example, 0603 is much better than 1206). On a related subject, I've been told that the metallic film on most surface-mounted resistors is generally placed on only one face of the package. Such one-sided parts exhibit more parasitic capacitance to ground, and less inductance, when turned "face down" rather than "face up." If you want these parts to appear with a particular orientation on your reels, you have to ask for it. Some engineers cut a little hole in the solid reference planes underneath the pads to reduce their parasitic capacitance. I am unaware of any inexpensive software or tools to help you determine the amount of cutting required, but I know microwave folks who use this trick all the time. They just try it and then adjust the hole size until it seems to work. Full-fledged, 3-D electromagnetic-field-simulation packages can tell you what size hole to use. It seems a shame, though, to have to buy such a complicated software package and spend all that time learning to use it when you could just try a hole to see what happens. On the other hand, if you need to solve the reference-plane-hole problem many times in many situations, a good 3-D field solver could save you a lot of trial-and-error time. |
POINT TO REMEMBER
- Densely packed component pads greatly reduce trace impedance.
5.3.1.8 How Close Is Close Enough?
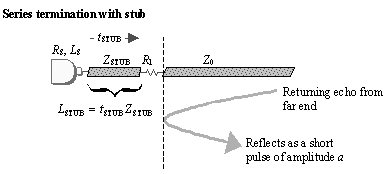
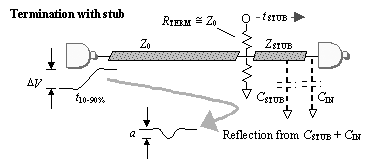
Article first published in EDN Magazine , April 9, 1998Let's say you can't fit your series termination in the ideal location, next to the driver. There isn't room. You have to place it a little further away than you'd like. Will it still work? A series termination resistor is supposed to absorb high-frequency energy, damping reflections on the net. To perform at its best, it must be directly connected to a very low impedance source, presumably your driver. Anything placed in series with the termination resistor changes its value, making it less effective. That includes the short pcb trace, or connection stub, that hooks the driver to the termination resistor. Applications that need very accurate termination (like clock lines) should take this effect into account. Fortunately, we can easily calculate the degradation due to a connection stub. As long as the stub delay is less than 1/3 of the signal risetime, the approximations given below will be accurate to within 25%. Place a series terminator no more than a small fraction of one risetime away from the driver. The connection stub (Figure 5.17), because it connects at one end to a low-impedance driver, acts like a little inductor L STUB . This stub inductance acts in series with the termination resistor R 1 , adding to the impedance of the termination. If you add the impedance of the stub j w L STUB to the resistor value R 1 , you get a reasonable model for the combined termination impedance. To this termination impedance you must also add the natural output resistance and inductance of the driver. I'll assume you have set up the value of R 1 so that it, plus the natural output resistance of the driver, together match the line impedance Z , so the overall model of the termination impedance looks like this: Equation 5.27
Figure 5.17. The returning echo from the far end encounters a composite load formed by the resistor R 1 , the inductance L STUB of the stub, plus the R S and L S of the driver.
The returning echo from the far end of the line, when it encounters termination network Z T , reflects a short pulse. This amplitude of the reflected pulse (as observed at the open -circuited far endpoint of the line) will be approximately Equation 5.28
That's the theory, except for one embellishment the stub affects the risetime of the first incident waveform by a tiny amount. Keep the stub delay less than 1/3 of the risetime and you will hardly see this risetime degradation. (Thanks to Tom Giovannini and Joe Cahill for reminding me to mention this).
The series termination in this case, even though it is adjusted for an ideal value of resistance , fails to completely damp the reflections because of the associated package and stub inductance. As a result, you may need to wait for the ringing to decay in this example before sampling the signal. Pay close attention to the length of your connection stub. Stub delays less than 1/3 of the signal risetime create residual reflections that can be approximated by [5.28]. Stub delays in excess of 1/3 of the signal risetime can create a significant resonance that grows rapidly with increasing trace length. Don't stretch your luck. If you want 20dB or more of reflected-wave attenuation, use a stub delay of no more than 1/6 the risetime, a very good low-inductance package, and an accurate carbon-composition or low-inductance metal film resistor. |
||||||||||||||||||||||||||||||
POINT TO REMEMBER
- Place a series terminator no more than a small fraction of one risetime away from the driver.
5.3.1.9 Placement of End Termination
High Speed Digital Design Online Newsletter , Vol 2, Issue 7Bob Haller writes I agree that series termination is a very effective way to eliminate SI problems on networks, and generating a simple expression to handle effectiveness based on placement is a great idea. Can you please address the stub length of parallel, terminated nets [for] both inline and downstream parallel termination? When I am performing parallel termination, it is often difficult to sequence the termination in the proper order (driver, long line, load, short stub, and termination). I have found that if the stub length is kept very short, and edge rates are not excessively fast, terminating in the alternate sequence (driver, long line, termination, short stub, and receiver) can be as effective and save significant routing channels when surface-mounted components are utilized (especially high pin count BGAs). Reply Thanks for your interest in High-Speed Digital Design . Great idea! When working with very fast edge rates, the sequencing of the end terminator and its associated load can make a measurable difference in signal quality. We can use "short stub" analysis to predict the effect. If you hook up a net in this sequence: driver, long line, terminator, short stub, and receiver, the additional short stub (which is open -circuited at both ends), will act as a small lumped-element capacitor (Figure 5.18). Figure 5.18. A dangling stub adds to the total load capacitance at the end of the trace, increasing the size of the reflected pulse.
This small capacitance of the stub, along with the parasitic input capacitance of the receiver pin, creates an imperfection in the termination network. When the first incident wave arrives from the driver, part of that wave, a small pulse, bounces off the imperfection and returns to the driver. The small reflected pulse travels backwards along the line to the driver, where it bounces again (off the low impedance of the driver output) and returns, one round-trip time later, to the receiver. What we observe at the receiver is an initial rising edge, followed one round-trip time later by a secondary pulse. If the initial reflected pulse is sufficiently small, all tertiary and subsequent events will be of negligible amplitude. Assuming the delay of the short stub is less than 1/3 of a risetime, you can model the amplitude of the reflected pulse: Equation 5.29
The relative accuracy of this formula is about +/- 25 percent.
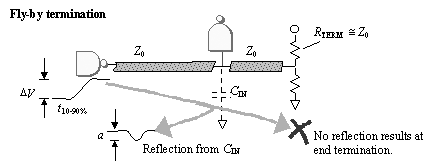
A stub whose length equals 10% of the signal rise (or fall) time, and whose impedance equals the impedance of the main signal trace, contributes a reflection 5% the size of the incoming step. A stub of 1/3 the length of the signal rise (or fall) time reflects on the order of 20% of the incoming step, destroying the effectiveness of the termination. A signal routed first to the receiver, then on to a parallel termination at the bitter end of the line, suffers no additional load capacitance other than the receiver itself (Figure 5.19). Figure 5.19. A fly-by termination suffers the capacitance of the receiver, but no additional reflection from the termination.
|
POINT TO REMEMBER
- Place an end terminator no more than a small fraction of one risetime from the end of the line.
5.3.1.10 Making an Accurate Series Termination
High Speed Digital Design Online Newsletter , Vol 4, Issue 14Bill Daskalakis writes I am aware that the driver output impedance or source impedance of a device may vary depending on whether it is in a high or low state. I have found that the source impedance may be as high as 200 ohms for the logic-1 state and as low as 20 ohms for a logic-0 state. How are you supposed to calculate an appropriate series termination when you have such a large variance in source impedance? Note: I assume you are supposed to calculate the series resistance from the equation R T = Z - R S ,
Reply Thanks for your interest in High-Speed Digital Design . Not only is there a wide variation in impedance from the high state to the low state, but there is an even wider variation from chip to chip, and between manufacturers of the same chip, and over the allowed operating temperature range, and over the allowed power-supply voltage range. The on-state output impedance of a partially turned-on FET is very difficult to control. It depends quadratically on the exact value of the gate-switching threshold, which varies wildly depending on everything else. Of course, you get huge variations in the output impedance. If you had access to +/- 20V supply rails that you could use to overdrive the FET gates in your I/O circuit (as is commonly done in switching-power-supply circuits), each FET would then turn on completely, producing an output resistance dependent on nothing but the bulk resistivity of your silicon and the size of the FET. As it is, most digital designs underdrive the gates, barely turning on the transistors , leaving the circuit quite sensitive to changes in its environment. You also are fighting the tendency of most chip designers to make the pull-up side of the totem-pole output circuit fundamentally weaker than the pull-down side. I'm not a chip design expert, but I believe this has something to do with the superior carrier mobility available within the N-channel FET on the bottom of the totem pole as compared to the P-channel FET on the top. A larger topside FET could ameliorate the problem, but only at the expense of significant additional output capacitance (which becomes a problem in the tri-state condition). As you have noticed, it is impossible given the specifications you have quoted to construct a series-terminated transmission line with sufficiently good termination to ensure first-incident-wave switching with a full-amplitude output signal. If you can afford to wait a few round-trip times, however, your gate performs admirably. Assuming you use transmission lines with a 65-ohm impedance, the gate output impedance will be mismatched by a ratio of no worse than 3.25:1 in either direction (either 200/65 or 65/20 equals about 3.2), producing a reflection coefficient no greater than 53%. After five round trips, the residual reflection will die down to less than 5%, at which point you can safely clock the line. That's the way you are supposed to use this gate. If you can't afford to wait, you need a more accurate series termination. What you must do to construct an accurate series-terminated configuration is use a driver with a much smaller output impedance. For example, consider the case of a driver whose output impedance varies from 1 to 10 ohms. Even though 10:1 is a huge variation in percentage terms, it is a small variation in absolute terms compared to 50 ohms. I may therefore place 45 ohms in series with this driver to produce an output structure whose impedance varies from 46 to 55 ohms, a pretty darn good match to a 50-ohm transmission line. Alternately, you could use a current-source output circuit having an output impedance much greater than 50 ohms and then place an accurate resistor in parallel with the output to control the source impedance. Either way, you end up using a good resistor to provide your well-controlled output impedance. In the bipolar world you have other options available. For example, an emitter-follower output circuit biased with a small but constant output current exhibits a fairly well-controlled output impedance. ECL drivers (if properly biased) make use of this property to synthesize an output impedance very close to 10 ohms. |
POINTS TO REMEMBER
- A low-impedance driver combined with a tight-tolerance resistor in series makes an accurate series termination.
- A high-impedance current-source driver combined with a tight-tolerance resistor in shunt across the driver also makes an accurate series termination.
5.3.1.11 Matching Pads
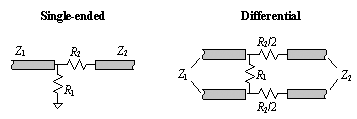
Article first published in EDN Magazine , December 21, 2000Suppose you are connecting a 75- W cable to a piece of 50- W test equipment, or perhaps you are hooking up a pc-board trace to an unusual cable. If the transmission lines on either side of the connecting junction are long (compared with the signal rise or fall time) and if the shift in impedance is significant, reflections from the junction may degrade your signal. To fix the degradation problem, you can add circuitry at the junction. The objectives for junction-matching circuitry vary according to your needs. Sometimes you want to cleanly pass signals in just one direction, the other direction, or both. Whatever the direction of signal flow, you want the signals to traverse the junction with minimal distortion, attenuation, and reflections. You can configure the circuit in Figure 5.20, called a resistive matching pad, to accomplish all of these objectives. The same basic circuit works for either single-ended or differential configurations. Figure 5.20. A resistive pad matches two circuits with characteristic impedances Z 1 and Z 2 .
In AC- coupled applications, in which no meaningful DC content exists, you can use a transformer to modify the circuit impedance. Examples of wideband applications with no meaningful DC content include audio, video, and some data signals specially coded to enforce an equal number of ones and zeros (such as Manchester data coding or 8B10B coding). The transformer is a good component to use for impedance translation, because by winding different numbers of turns on the primary and secondary of the core , you can amplify (or attenuate) the voltage at the expense of an opposite change in current. Unfortunately, transformers don't work at DC. In narrowband applications, such as carrier-based AM or FM radio, you can sometimes use resonant-circuit tricks to accomplish impedance transformation. A classic example is the resonant pi filter. It can accomplish voltage amplification (or attenuation) over a narrow band of frequencies but not over a wide band . Random digital data, whose spectrum spreads across a vast range from DC to daylight , renders useless all standard narrowband and AC-coupling tricks. The only passive circuits that guarantee good impedance translation for wideband signals are resistive pads. The only passive circuits that guarantee good impedance translation for wideband signals are resistive pads. You can configure the matching pad shown in Figure 5.20 for left-to-right transmission, right-to-left transmission, or both. Table 5.6 presents the required component values and lists the performance for each application. Each row of Table 5.6 shows values for R 1 and R 2 . The signal gain G (never bigger than unity) and reflection coefficient G (bounded by 1) are then given for signals traveling in either direction. Without loss of generality, the table assumes that Z 1 < Z 2 . (If your circuit is the other way around, then look at Figure 5.20 in a mirror.) Table 5.6. Matching Pad Performance
When you configure the circuit for optimal operation in one direction, the reflection coefficient in the opposite direction is not very good. In fact, it's worse than with a raw, unmatched junction. Sometimes such lopsided performance is acceptable. For example, with a good source-terminated network (source on the left), when the driver emits a fresh edge, you don't really care what bounces off the junction. The first bounce merely returns to the source termination and dies. You do, however, care about the signals that reach the end and then bounce off the massive open-circuited endpoint. These signals, on their return trip, take a second pass across the junction, and the reflection coefficient from right to left mostly determines the performance of the system in this circumstance. For a source-terminated application with Z 1 < Z 2 , choose the optimal right-to-left pad. For an end-terminated driver on the same line, the optimal left-to-right pad works best. The both-ends termination (using both source and end-termination) is the least sensitive of all configurations to reflections at the junction. With both ends terminated, your circuit may not need a matching network at all. To match two differential circuits with differential impedances Z 1 and Z 2 respectively, place R 1 directly between the two conductors of impedance Z 1 . Then split R 2 into two resistors, each of value R 2 /2, and put one in series with each conductor of impedance Z 2 . |
||||||||||||||||||||||||||||||||||||||||||||||||
Postlog: Several readers pointed out that any signal having no DC component can be converted from one impedance domain to another using a transformer. Signals having no DC component include a 50 percent duty-cycle clock, Manchester-coded data, and data subject to other specialized codes like 8b10b that have the property of generating equal numbers of 1s and 0s. Even signals that have a DC component may be passed through a transformer provided the receiver is equipped with DC level restoration circuitry (see Section 5.2.1, "SONET Data Coding").
POINT TO REMEMBER
- Impedance translation over any band that includes DC is accomplished using a resistive pad.
5.3.2 Pcb Crosstalk
5.3.2.1 Purpose of Solid Plane Layers
Crosstalk in pcb applications is dramatically reduced by the presence of a solid reference plane. That's the primary reason for using solid planes in high-speed digital products. The reference planes can carry any DC voltage, including ground, V CC , or anything else. Because crosstalk is an AC effect, the DC voltage on the reference plane makes no difference. What does matter, however, is that the plane nearest the signal trace must be continuous everywhere underneath the trace. Where a trace jumps through a signal via from layer to layer, changing reference planes, the planes must be interconnected with a suitably low impedance near the signal via.
The planes act to promote an eddy current that flows in opposition to, and directly underneath, the current flowing on every individual signal trace. The eddy current creates its own magnetic field that opposes the magnetic field from the signal current. The electromagnetic field from the signal current, combined with the equal-but-opposite field from the eddy current, creates an overall field pattern that falls off quite rapidly with increasing distance. The overall result is that crosstalk between two parallel traces varies strongly with trace separation and with the trace height above the plane. Either an increase in trace separation or a decrease in trace height will markedly reduce crosstalk.
Slots or cuts in the reference plane made perpendicular to a signal trace interrupt the formation of eddy currents, usually resulting in a marked increase in crosstalk, especially if the slot or cut passes directly underneath the trace.
POINT TO REMEMBER
- Solid reference planes exist to control crosstalk.
5.3.2.2 Variations with Trace Geometry
In a microstrip configuration with an underlying solid reference plane the crosstalk varies approximately quadratically with both trace separation and trace height. This means that a 10% increase in separation (or a 10% decrease in trace height) will decrease crosstalk by roughly 20%. A doubling of distance (or halving of height) decreases crosstalk by a factor of about four.
In stripline configurations the variation can be even stronger. Separation and height are your two greatest weapons when it comes to fighting crosstalk.
For example, suppose you have two microstrips, each 100- m m (4 mils) above a solid reference plane. Separating the two microstrips by 10 mm (400 mils) of white space (a separation-to-height ratio of 100:1) limits the crosstalk to something on the order of 1 part in 10,000 (80 dB). This is more crosstalk immunity than needed for almost any ordinary digital logic purpose. Digital traces of similar amplitudes, even at extremely high speeds, do not need to be isolated from each other by cuts or moats in the reference plane. They just need to be routed with an appropriate spacing.
A two-dimensional field solver does a terrific job of estimating crosstalk between traces routed over a common solid reference plane. Using a field solver is the best way to estimate crosstalk for general digital purposes. Unfortunately, the assumptions behind a two-dimensional solver break down at any holes, slots, or gaps in the continuity of the planes, especially if those holes cross the path of either the victim or aggressor trace. Any time you see a trace crossing hole or gap in the plane you can expect a tremendous upsurge in crosstalk and radiation.
POINTS TO REMEMBER
- Crosstalk varies strongly with trace separation and with the trace height above the reference planes.
- A field solver is the best way to estimate crosstalk for general digital purposes, provided that no holes, slots, or gaps in the planes cross the path of either the victim or aggressor trace.
5.3.2.3 Directionality
Crosstalk in pcb traces is highly directional. A fast-edged signal propagating in a microstrip trace produces less crosstalk in the forward direction than in the reverse (see following sections about NEXT and FEXT). When measured as shown in Figure 5.21, the forward and reverse crosstalk waveforms differ noticeably.
Figure 5.21. Crosstalk is directionalthe forward and reverse crosstalk waveforms differ (voltage vs. time shown at each end).
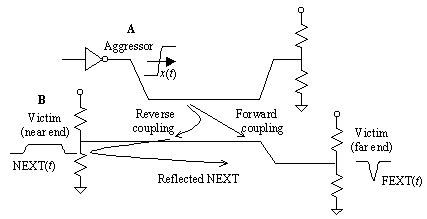
Whether initially headed in the forward or reverse direction, crosstalk reflects and bounces off any imperfections in the transmission structure, often ending up at both ends of the line. It is therefore difficult (and meaningless) in some configurations to bother distinguishing between the two forms of crosstalk. What matters in most cases is that you can exert powerful control over the coupled crosstalk amplitude by changing either the trace separation or height.
Due to the differences in NEXT and FEXT, and the way crosstalk bounces off the source and load, the timing and polarity of coupled crosstalk depends on whether the lines run in the same direction, or opposite directions.
POINTS TO REMEMBER
- Crosstalk is highly directional.
- Whether initially headed forward or backward, crosstalk reflects and bounces off any imperfections in the transmission structure, often ending up at both ends of the line.
5.3.2.4 NEXT: Near-End or Reverse Crosstalk
A fast-changing signal propagating along a transmission line couples some portion of its power into the adjacent traces, inducing signals that travel in both directions along the victim traces. The portion of the coupled power that flows backwards along the victims in a direction opposite to the forward progress of the aggressive signal is called reverse crosstalk . Reverse crosstalk is also called near-end crosstalk, or NEXT.
A pair of parallel traces having zero length exhibit no crosstalk of any kind. As the length of the parallel overlap is gradually lengthened, however, the amplitude of reverse crosstalk at first grows in proportion to length. The growth continues until the trace delay associated with the parallel overlap exceeds half the signal risetime t r . Beyond this point the reverse-crosstalk amplitude saturates at a maximum step height. Lengthening the line beyond t r /2 lengthens the duration of the reverse-crosstalk pulse, but not its amplitude. In response to a positive step input at the aggressor, the near-end crosstalk waveform appears as a long, low rectangle with a flat top. The initial rise time and final fall time of the near-end crosstalk waveform are the same as the rise time of the source. The duration of the near-end crosstalk waveform equals twice the delay of the parallel overlap between aggressor and victim plus one source risetime.
The maximum peak height of the reverse-crosstalk waveform at saturation, expressed as a fraction of the amplitude of the aggressive step, is called the reverse-crosstalk coupling coefficient , or NEXT coefficient .
Once you reach a length sufficient to saturate the reverse crosstalk, further extension of the length of overlap does not affect the amplitude of the reverse crosstalk. Management of crosstalk by controlling the length of parallelism does not work in systems where the line delay exceeds t r /2.
In typical pcb applications involving sub-nanosecond signals, and especially on serial links, where the line delay greatly exceeds the signal risetime, the reverse crosstalk almost always achieves its maximum, saturated value.
The value of the NEXT coefficient is not determinable by analytic formula (although it has been approximated in closed-form expressions applicable for limited conditions). It is best found by 2-D field simulation. Examples showing single-ended to differential NEXT for a stripline configuration appear in Section 6.11.6, "Reducing Local Crosstalk."
POINTS TO REMEMBER
- For parallel traces shorter than half the signal risetime, near-end crosstalk varies in proportion to the length of parallelism.
- For parallel traces longer than half the signal risetime, near-end crosstalk saturates at a maximum level. The ratio of crosstalk to aggressive step-size at saturation is the NEXT coefficient.
- Saturated NEXT looks like a long, low rectangle with a flat top and a duration equal to twice the trace delay plus one source risetime.
5.3.2.5 FEXT: Far-End or Forward Crosstalk
The portion of the coupled power that flows forward along a victim trace in a direction coincident with the forward progress of the aggressive signal is called forward crosstalk . Forward crosstalk is also called far-end crosstalk, or FEXT.
Forward crosstalk grows with trace length, saturating only when the amplitude of the coupled signal grows to a magnitude comparable with the aggressor. The shape of the coupled pulse is proportional to the derivative of the aggressor signal. In response to a positive step input on the aggressor, FEXT looks like a short pulse with duration equal to the signal risetime t r .
The FEXT coupling coefficient may be expressed as a dimensionless fraction, where it is expected that you multiply that fraction times the line delay (accounting for length) and then divide by the risetime t r (accounting for differentiation). Alternately, given a fixed risetime t r (or for sine wave analysis, a fixed frequency f ), you may choose to work with FEXT in units like percent crosstalk per meter.
In a microstrip trace having a delay equal to half the signal risetime ( t r /2) the peak height of the FEXT waveform is substantially less than the NEXT waveform.
The value of the FEXT coefficient is not determinable by analytic formula. It is best found by 2-D field simulation.
In a microstrip configuration the mutual capacitive coupling between adjacent traces is generally weaker than the mutual inductive coupling, driving the FEXT coefficient negative. Negative FEXT means that in response to a positive rising edge the FEXT appears as a negative pulse (and in response to a negative falling edge the FEXT appears as a positive pulse).
In a stripline trace (or any parallel configuration embedded in a homogeneous dielectric medium) the fine balance between inductive and capacitive coupling produces almost no observable forward crosstalk. In a stripline trace the coupled crosstalk initially flows almost entirely in the reverse direction, although it may quickly bounce off imperfections in the transmission structure and end up generating interference at the far end of the line anyway.
POINTS TO REMEMBER
- Far-end crosstalk varies in proportion to the trace length.
- FEXT looks like a short pulse with a duration equal to the source risetime.
5.3.2.6 Special Considerations
You can arbitrarily reduce FEXT or NEXT by separating the aggressor and victim traces, or by reducing their height above the planes (and making a proportional reduction in trace width to keep the impedance constant). Unfortunately, boards often lack sufficient space to achieve the desired reduction by spacing alone. In that case you'll want to know how to cheat.
Suppose serial-link connections A and B are oriented in the same direction, both driven by low-impedance sources (Figure 5.21). A fast-changing signal on trace A induces NEXT on trace B . The NEXT coupled into B travels backwards along trace B towards its driver (represented by resistors on the left). When the NEXT encounters the driver at the left end of B it will reflect, eventually ending up at the far end of trace B . The reflected signal is called reflected NEXT . The size of the reflected NEXT is determined by the product of the original NEXT amplitude times the reflection at driver B . At the right end of A you see both the FEXT and the reflected NEXT, superimposed.
A series termination at driver B would establish a reflection coefficient of zero at driver B , eliminating the reflected NEXT just described. Although this sounds helpful, the series termination would not by itself eliminate the complete effect of NEXT. To see why you must follow the progress of the aggressive signal on A all the way to its conclusion.
The main body of the aggressive signal on A is driven towards the right. Depending on the termination scheme employed by net A , this signal may bounce off the far endpoint of A , returning to the left. Along the way back towards the source the leftward-moving reflected signal creates both forward and reverse crosstalk on B . The forward crosstalk travels along the same direction as the leftwards-moving signal, while the reverse crosstalk travels in the opposite directionthat is, back to the right! This is the second form of reflected NEXT that can cause a disturbance at the far end of the victim net.
To prevent the first form of reflected NEXT you need a series termination at source B . To prevent the second form of reflected NEXT you need an end termination on net A . The end termination prevents the generation of the leftward-moving reflection, cutting off the possibility of further crosstalk. The combination of source-termination on the victim net with end-termination on the aggressor produces a pair of traces that, to first order, are immune to NEXT.
Unfortunately, the reciprocal combination (source-terminated aggressor and end-termination victim) does not work to reduce NEXT.
In the context of a number of parallel lines the only feasible way to eliminate all NEXT combinations is to equip every line with both near-end and far-end terminations, a combination burdened with the disadvantage of halving the received signal amplitude.
The FEXT situation is different. To gain immunity to FEXT, you must use stripline traces. The FEXT coefficient for a pair of raw, unloaded striplines is always zero (see Section 5.3.2.5, "FEXT: Far-End or Forward Crosstalk").
From the above argument you may conclude that of all common pcb structures the both-ends-terminated stripline is the least susceptible to crosstalk.
In a practical circuit you will never completely eliminate crosstalk, because even the tiniest imperfections in either aggressor or victim create reflected signals that eventually flow towards endpoint B . For example, a small reflection on the aggressor trace produces a reverse-flowing waveform. The NEXT from this reverse-flowing signal then flows on the victim in a direction headed, once again, towards the far end.
Also, the cancellation of FEXT depends on a delicate balance between inductive and capacitive crosstalk within the transmission structure. This fine balance applies to any transmission structure constructed in a homogeneous dielectric environment and having a uniform cross section. If the transmission parameters are artificially modified due to surface roughness or other imperfections, the ideal balance between voltage and current is disturbed, creating nonzero FEXT. Vias, connectors, and other loads that disturb the trace impedance all create FEXT.
Crosstalk in a bus can never be eliminated, but it can be substantially abated through the use of both-ends terminated striplines.
Now suppose links A and B proceed in opposite directions. In this case the NEXT from A appears directly at the input to B , an effect that cannot be eliminated by fancy footwork with terminations. Accordingly, for best performance (i.e., maximum packing density on a backplane), one might select both-ends-terminated striplines, grouping all tracks with the same orientation together and providing extra spacing between traces with opposite orientations.
I should point out that in a synchronous bus FEXT has almost no impact, as it dissipates quickly after each rising edge, so that in practice a both-ends-terminated microstrip bus performs equally as well as a both-ends-terminated stripline bus.
In most cases it is the crosstalk measured at the far end of a trace that matters. If you are producing a full-duplex link ( utilizing a hybrid circuit), however, the near-end reflections and NEXT issues discussed in Section 8.3, "UTP Noise and Interference," will also apply to your situation.
POINT TO REMEMBER
- The both-ends terminated stripline architecture greatly reduces, but does not completely eliminate, both FEXT and NEXT.
5.3.2.7 Directionality of Crosstalk
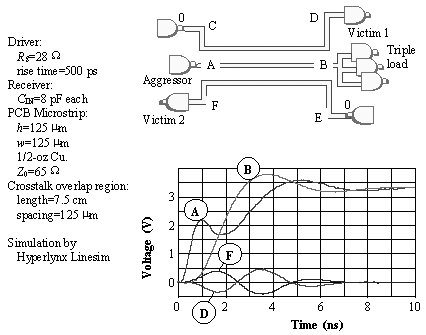
Article first published in Electronic Design Magazine , August, 1997Crosstalk is a fact of life in modern digital systems. We can't eliminate it, but it's our job to figure out how to control it, manage it, and just plain live with it. Consider the circuit in Figure 5.22. In the terminology of crosstalk, the gate at position A is the aggressor, and the gates at positions D and F are the victims. Gates C and E remain stuck at zero for the duration of this discussion. Figure 5.22. Crosstalk for short, heavily-loaded lines is highly directional.
Whenever aggressor A changes state, we observe a characteristic crosstalk waveform at both victims. Those of you doing dense, high-speed designs probably recognize this all-too-familiar scenario. One of the fascinating things about crosstalk is its directionality. Crosstalk waveforms are a function of the orientation of the driver and receiver. For example, in Figure 5.22 the two victim circuits have opposite orientations. In response to a rising edge on the aggressor, the waveforms at D and F display opposite polarities. Crosstalk is directional. The differing polarities suggest that we are not dealing with capacitive crosstalk. Many digital engineers assume that crosstalk is primarily a capacitive effect. It isn't. Mutual capacitance acting alone would cause the same polarity of crosstalk at both endpoints. The differing polarities indicate that the interference is due (at least in part) to mutual inductive coupling. That's the same kind of coupling you get in a transformer. Everyone knows that reversing the leads on the primary winding of a transformer will reverse the polarity of the voltage on the secondary. Coupled pcb traces act in much the same way. If you think of each pcb trace as a little loop of current, you can see how the "crosstalk" transformer works. First, imagine current from the gate at position A flowing out through the aggressor trace to the load at B . From there the current returns, along the power and ground system, back to the source at A . The aggressive current thereby makes a loop. Think of this loop as the primary winding of a transformer. One secondary winding of that same transformer lies nearby. It is the loop formed starting with the gate at position C , moving out along the victim trace to the load, and back along the power and ground system, returning to the gate at C . The primary and secondary loops acting together behave almost exactly like a weakly coupled, single-turn transformer. Because the orientation of the bottom circuit E F opposes the top circuit C D , the mutual inductive crosstalk captured at endpoint F is exactly opposite that captured at D . This behavior corresponds to the action of a transformer having two secondaries wound in opposite directions. One receives a positive signal, the other, negative. The existence of transformer-type mutual inductive coupling between traces has profound implications for digital designs. For one thing, it implies that crosstalk varies depending on the applied load. For example, Figure 5.22 assumes a short pcb trace such that the driver and load behave as if directly coupled. In this case the aggressor current varies strongly as a function of the applied load. The heavier the load, the more aggressor current the circuit draws and the more crosstalk it generates. The triple-loaded network in the figure therefore generates more crosstalk than would a similar net, with a similar topology, having only one load. In contrast, a simple mutual-capacitance coupling model incorrectly predicts a decrease in crosstalk as loads are added to the circuit due to the smaller d v /d t present in the aggressive circuit when heavily loaded. The loading effect is particularly acute when driving banks of SIMM memory modules. Such traces tend to be very short, but heavily loaded. When you insert the second SIMM module, the drive current rises markedly, creating noticeably more crosstalk. If you are trying to debug a crosstalk problem on a dense multilayer board, knowledge of how trace loading affects crosstalk can help you understand, and fix, crosstalk problems. If you are trying to manage crosstalk from first principles so it comes out right on the first spin, look into the new crosstalk prediction tools that feature IBIS I/O modeling. Many of these new tools are capable of calculating crosstalk, including the loading effects, in an automated, highly efficient manner. |
POINT TO REMEMBER
- Both voltage and current affect crosstalk.
Fundamentals
- Impedance of Linear, Time-Invariant, Lumped-Element Circuits
- Power Ratios
- Rules of Scaling
- The Concept of Resonance
- Extra for Experts: Maximal Linear System Response to a Digital Input
Transmission Line Parameters
- Transmission Line Parameters
- Telegraphers Equations
- Derivation of Telegraphers Equations
- Ideal Transmission Line
- DC Resistance
- DC Conductance
- Skin Effect
- Skin-Effect Inductance
- Modeling Internal Impedance
- Concentric-Ring Skin-Effect Model
- Proximity Effect
- Surface Roughness
- Dielectric Effects
- Impedance in Series with the Return Path
- Slow-Wave Mode On-Chip
Performance Regions
- Performance Regions
- Signal Propagation Model
- Hierarchy of Regions
- Necessary Mathematics: Input Impedance and Transfer Function
- Lumped-Element Region
- RC Region
- LC Region (Constant-Loss Region)
- Skin-Effect Region
- Dielectric Loss Region
- Waveguide Dispersion Region
- Summary of Breakpoints Between Regions
- Equivalence Principle for Transmission Media
- Scaling Copper Transmission Media
- Scaling Multimode Fiber-Optic Cables
- Linear Equalization: Long Backplane Trace Example
- Adaptive Equalization: Accelerant Networks Transceiver
Frequency-Domain Modeling
- Frequency-Domain Modeling
- Going Nonlinear
- Approximations to the Fourier Transform
- Discrete Time Mapping
- Other Limitations of the FFT
- Normalizing the Output of an FFT Routine
- Useful Fourier Transform-Pairs
- Effect of Inadequate Sampling Rate
- Implementation of Frequency-Domain Simulation
- Embellishments
- Checking the Output of Your FFT Routine
Pcb (printed-circuit board) Traces
- Pcb (printed-circuit board) Traces
- Pcb Signal Propagation
- Limits to Attainable Distance
- Pcb Noise and Interference
- Pcb Connectors
- Modeling Vias
- The Future of On-Chip Interconnections
Differential Signaling
- Differential Signaling
- Single-Ended Circuits
- Two-Wire Circuits
- Differential Signaling
- Differential and Common-Mode Voltages and Currents
- Differential and Common-Mode Velocity
- Common-Mode Balance
- Common-Mode Range
- Differential to Common-Mode Conversion
- Differential Impedance
- Pcb Configurations
- Pcb Applications
- Intercabinet Applications
- LVDS Signaling
Generic Building-Cabling Standards
- Generic Building-Cabling Standards
- Generic Cabling Architecture
- SNR Budgeting
- Glossary of Cabling Terms
- Preferred Cable Combinations
- FAQ: Building-Cabling Practices
- Crossover Wiring
- Plenum-Rated Cables
- Laying Cables in an Uncooled Attic Space
- FAQ: Older Cable Types
100-Ohm Balanced Twisted-Pair Cabling
- 100-Ohm Balanced Twisted-Pair Cabling
- UTP Signal Propagation
- UTP Transmission Example: 10BASE-T
- UTP Noise and Interference
- UTP Connectors
- Issues with Screening
- Category-3 UTP at Elevated Temperature
150-Ohm STP-A Cabling
- 150-Ohm STP-A Cabling
- 150- W STP-A Signal Propagation
- 150- W STP-A Noise and Interference
- 150- W STP-A: Skew
- 150- W STP-A: Radiation and Safety
- 150- W STP-A: Comparison with UTP
- 150- W STP-A Connectors
Coaxial Cabling
- Coaxial Cabling
- Coaxial Signal Propagation
- Coaxial Cable Noise and Interference
- Coaxial Cable Connectors
Fiber-Optic Cabling
- Fiber-Optic Cabling
- Making Glass Fiber
- Finished Core Specifications
- Cabling the Fiber
- Wavelengths of Operation
- Multimode Glass Fiber-Optic Cabling
- Single-Mode Fiber-Optic Cabling
Clock Distribution
- Clock Distribution
- Extra Fries, Please
- Arithmetic of Clock Skew
- Clock Repeaters
- Stripline vs. Microstrip Delay
- Importance of Terminating Clock Lines
- Effect of Clock Receiver Thresholds
- Effect of Split Termination
- Intentional Delay Adjustments
- Driving Multiple Loads with Source Termination
- Daisy-Chain Clock Distribution
- The Jitters
- Power Supply Filtering for Clock Sources, Repeaters, and PLL Circuits
- Intentional Clock Modulation
- Reduced-Voltage Signaling
- Controlling Crosstalk on Clock Lines
- Reducing Emissions
Time-Domain Simulation Tools and Methods
- Ringing in a New Era
- Signal Integrity Simulation Process
- The Underlying Simulation Engine
- IBIS (I/O Buffer Information Specification)
- IBIS: History and Future Direction
- IBIS: Issues with Interpolation
- IBIS: Issues with SSO Noise
- Nature of EMC Work
- Power and Ground Resonance
Points to Remember
Appendix A. Building a Signal Integrity Department
Appendix B. Calculation of Loss Slope
Appendix C. Two-Port Analysis
- Appendix C. Two-Port Analysis
- Simple Cases Involving Transmission Lines
- Fully Configured Transmission Line
- Complicated Configurations
Appendix D. Accuracy of Pi Model
Appendix E. erf( )
Notes
EAN: N/A
Pages: 163
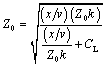
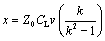
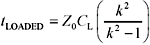
 r = 4.3, so v = 1.44610 8 m/s, and
r = 4.3, so v = 1.44610 8 m/s, and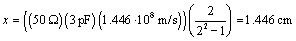
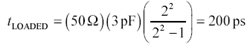
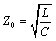
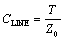
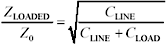
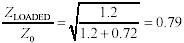
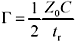

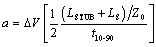
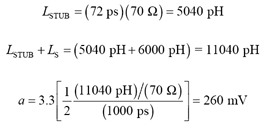
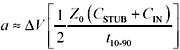
 R direction
R direction
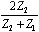
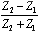
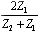
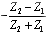
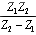
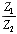
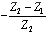
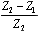
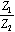
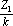
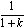
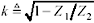 , Z 1 must be less than Z 2
, Z 1 must be less than Z 2