Rules of Scaling

Digital designers do not restrict their attention to any particular range of power, impedance, physical size, or frequency. Unlike designers in other application areas, the field of digital design cuts across many orders of magnitude of the frequency, power, and size domains. For example, a designer of battleship rudder control systems might build a whole career on an understanding of large electromechanical and hydraulic machinery in the frequency range of from 0.01 to 1 Hz. An audio engineer, on the other hand, might specialize in the 10 to 100,000 Hz band , working with desktop-size amplifier boxes. Digital designers know no such bounds. Every few years their horizon expands, taking them to ever-higher realms of frequency and to ever-smaller physical scales of operation. Digital systems today span a vast array of physical scales , from integrated circuit dimensions smaller than one micron to intercontinental distances, and a vast array of frequencies, from deep-sea submarine communications at 0.1 Hz to fiber- optic links running at 100 GHz and beyond.

If you wish to exist in such a world, you must make your knowledge portable so that you may more easily move from one domain to another. The theory that makes this possible is the mathematical theory of scaling.

The rules of scaling (listed below) show how to transform one system into an equivalent system operating at a different scale. This scaling may distort the physical sizes or the component values of the circuit elements involved, but the principles of circuit operation will remain the same: Low-impedance series elements in the first system will translate into (relatively) low-impedance elements in the new system, and so forth. A system that transfers power efficiently (or blocks the transmission of power) at one scale may be transformed into a new system that performs the same function on a different scale.

You can use these rules to establish analogies between systems that are known to work in one range of power, impedance, physical size, and frequency and others that you may wish to construct on a different scale.

1.3.1 Scaling of Physical Size

When you change the physical dimensions of a distributed circuit, modifying all geometrical dimensions x , y , and z by a common factor k , without changing either the electric permittivity or the magnetic permeability , you find that all inductances change by a factor of k and all capacitances change by the same factor.

If the circuit is passive and lossless (that is, composed only of inductive and capacitive effects, with no resistances) it will have been scaled in time, whereby the new circuit should behave the same as the old circuit, only its step response stretched (or compressed) in time by the factor k . A network-analyzer plot of the new system will show the same frequency response as the old, only shifted in frequency by a factor of 1/ k . A resonance at frequency f 1 in the original circuit appears at frequency f 1 / k in the new circuit. As a consequence, physically enlarging a system of physical conductors lowers its resonant frequencies, while shrinking the system physically raises them.

This principle of physical scaling explains why high-frequency microwave connectors must be made so darn smallthe tiny dimensions are required to push the parasitic resonances up to frequencies above the bandwidth of the signal.

The presence of significant resistance in a circuit complicates the situation. When a circuit is physically scaled, a new resistor 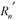replaces each resistor R n in the old circuit. It would be nice if each new resistance 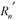operating at the new frequency f/k presented the same impedance as the old resistance R n operating at the old frequency f :

Equation 1.10

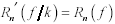
If [1.10] held true, the new circuit would behave identically to the old, except for the factor-of- k dilation (or compression) of time. If you are dealing merely with lumped-element components , then resistive scaling is trivialjust don't change the values of resistances in the circuit.

Unfortunately, if you are trying to model damping effects due to the skin-effect resistance of physical conductors, the resistive scaling becomes more complicated. Here's how it works.

At frequencies below the onset of skin effect the bulk resistance of a conducting object varies with its length and inversely with its cross-sectional area . When you scale all physical dimensions by k , the length goes as k , while the inverse of cross-sectional area goes as 1/ k 2 , with the result that bulk resistance changes as 1/ k . This effect changes the losses within the circuit in such as way that the new circuit will not necessarily perform like the old.

At frequencies above the skin-effect threshold the AC resistance of a long, skinny object like a wire varies with three terms: length , circumference , and frequency . AC resistance varies proportional to length, inversely with circumference (not cross-sectional area), and because of changes in the skin depth, proportional to the square root of frequency. When you change all physical dimensions by k and simultaneously change the operating frequency by a factor of 1/ k , the length goes as k , the inverse of circumference goes as 1/ k , and the skin depth term goes as 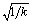. The net result is that skin-effect resistance appears modified in the new circuit by the ratio .

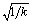The difficulties associated with resistive scaling of conductors can be fixed (theoretically) by building the new conductors from a new material, where the conductivity of the new material is reduced from the old by a factor of k . This substitution causes the resistance to remain unchanged (which is what you want) at any scale factor. While this theory is intellectually appealing, it does not appear to have much practical significance except for the idea that one could make 1:4 blowups of small copper structures using brass (which has 1/4 the conductivity of copper ), and they would have exactly the same electrical properties as the original, including the percentage penetration of skin depth, and so on.

Fortunately, in many problems where this rule of scaling applies, the resistance hardly matters. For example, whenever you are working with low-loss elements (like the metal lead-frame on a semiconductor package), the resistance is vanishingly small in the first place, with the result that physical scaling changes mostly just the inductive and capacitive parameters. Thus, it is practical to manufacture a 1:100 enlargement of a portion of a chip package and directly measure the inductance and capacitance of the enlarged structure. The values of L and C corresponding to the IC structure will be precisely 100 times less.

The rule of physical scaling applies well to low-loss conducting structures like metal plates, conducting wires, connector pins, and semiconductor packages. This rule is valid over any range of physical scales for which useful conducting objects may be constructed . It breaks down for certain structures near the atomic level, for which the conducting surfaces cannot be scaled due to the inherent quantization of atomic matter. As far physicists know, this law applies to structures of galactic dimensions, although such structures have not been tested to verify conformance with the rule.

Examples of physical scaling

An SOIC package, being generally smaller than a DIP package, exhibits less lead inductance.

A big via has more parasitic capacitance than a small via.

1.3.1.1 Scaling Inductors

Given two different sized inductors built from the same material and having the same geometry, the larger of the two will have more inductance. At any fixed frequency f below the onset of the skin effect the resistance of the larger inductor will be less. At frequencies above the onset of the skin effect the resistances of the two inductors, determined by the ratio of the length to the circumference of their conductors, will be the same. In either case the quality factor ( Q ), being related to the ratio j w L / R SERIES , will be markedly better in the larger inductor.

Unfortunately, the larger inductor will also have more parasitic capacitance, reducing its parallel-resonant frequency inversely with the scale factor.

1.3.1.2 Scaling Transmission-Line Dimensions

If we apply the rule of physical scaling to the problem of transmission lines, an interesting result appears. Imagine a printed-circuit board (pcb) trace having a certain length, width, thickness , and height above ground. Now scale all physical dimensions by the common factor k . According to the rule of physical scaling, the resulting structure will possess a total inductance (measured at low frequencies with the far end shorted) and capacitance (measured at low frequencies with the far end open -circuited) of k times the original values. Also note that the total length will now be k times the original length. Looking at the ratio of total inductance to length, note that their ratio is unaffected, because the total inductance value and the length value scale similarly. The same thing happens to the ratio of total capacitance to length: it is unaffected by physical scaling.

To make the next leap in this argument you need to recall that the impedance and per-unit-length delay parameters are functions of the per-unit-length values of inductance and capacitance for the line. If, as a result of scaling, you have failed to affect the per-unit-length values of inductance and capacitance, then you will also have failed to affect the impedance and per-unit-length delay.

This is the fascinating result: scaling the width, height, and thickness of a transmission line by a common factor k has no effect on the impedance or per-unit-length delay. You may have affected the resistive losses in a peculiar fashion, but not the impedance or delay.

This result applies to transmission lines operated in the LC mode, where the series inductance greatly exceed the series resistance, and the shunt capacitance greatly outweighs the effect of shunt conductance , conditions generally true in most pcb-trace problems.

POINTS TO REMEMBER

• Large objects have more inductance and capacitance than small ones.
• High-frequency connectors must be very small to push the parasitic resonances up to frequencies above the bandwidth of the signal.
• Simultaneously enlarging the height and width of a transmission line has no effect on the characteristic impedance or per-unit-length delay.

 

1.3.2 Power Scaling

In a linear circuit, one may amplify (or attenuate) the voltage and current levels at all points within a circuit simply by scaling all independent voltage and current sources (including fixed DC sources) by a common factor k . Assuming all impedances remain fixed, this adjustment multiplies all power levels within the circuit by the factor k 2 . Dependent sources need not be adjusted, as they will automatically change their output levels in response to a change in stimulus.

In a nonlinear circuit, to obtain the same scaling effect, one must also scale all I-V curves for nonlinear elements according to the following rule: Each point in the ( i , v ) relation for the original element is mapped to a new point ( ki,kv ) representing the new element. Such scaling of the nonlinear properties may in general not be physically possible. The control laws for nonlinear controlled sources must also be similarly scaled. The resulting circuit will behave identically to the first, remembering that all voltages and currents will be modified by the factor k and power will be modified by a factor k 2 .

This rule applies to all circuits. The possible range of scaling is limited on the low-power end by the quantization of electrical charge. That limit is reached in some advanced semiconductor memory storage circuits. On the high-power end power scaling is limited by the maximum current density that may be supported by the good conductors in the circuit and also by the maximum power density that may be dissipated by any resistive or semiconducting elements within the circuit. For example, within an integrated circuit at gate dimensions of 0.35 m m or less, the problem of aluminum atom migration commonly limits the total current that may be carried by a thin aluminum trace. [1] The aluminum migration problem, while severe at the physical scale of an integrated circuit, causes no difficulties at the scale normally used for pcb production.

[1] The passage of electrons at incredibly high current density though a tiny aluminum wire can actually knock some of the aluminum atoms out of place, leading to eventual failure of the conductor.

For another example, the power density present at the active transmitting facet of a high-performance 1 mW data communications laser diode is greater than that of an electric oven-heating element on full broil. Attempts to scale up the power beyond this limit result mostly in melted laser diodes.

Example of power scaling

All other specifications being equal, 3.3V logic dissipates less than half the power of 5V logic.

POINT TO REMEMBER

• Lower-voltage logic is remarkably power-efficient.

 

1.3.3 Time Scaling

This is one of the more interesting rules of scaling, as it indicates how a circuit must be modified to obtain high-speed operation.

In a linear , time-invariant , passive circuit, changing all inductances and capacitances by a fixed factor k , leaving the resistances fixed, scales the system step response in time. The new step response is the same as the old in every respect except for a scaling of the independent variable, time, by a factor of k . If the inductances and capacitances are increased, the new response is slower than the old. If the inductances and capacitances are made smaller, the new response is faster than the old.

Time scaling does not change the power, voltage, or current levels within a circuit. It merely stretches the scale of time for all voltage and current waveforms in the original circuit. This principle is the key to speeding up digital systems. Before we delve into a detailed example showing the time-scaling principle at work, let's look at some pesky details having to do with nonlinear and time-varying circuits.

If a passive circuit is nonlinear, and the nonlinear elements are assumed to be instantaneous in their actions (or a composite of instantaneous nonlinear effects combined with other linear, time-invariant circuits), the same result holds. No modification is needed to the I-V characteristics of the nonlinear components, although a scaling of the reactive elements internal to each nonlinear model is required. For example, if you wish to scale the basic SPICE level-1 model of an individual FET, the basic equations governing the conductance of the gate region need not be modified, but all parasitic inductances and capacitances must be scaled. Within a physical semiconductor structure such as a FET, other effects, such as the transit time for electrons drifting across the gate region, also require adjustment.

If the system includes time-varying voltage or current sources, a time dilation (or compression) of all the independent source voltages (or currents), in conjunction with time scaling of all other reactive elements in the circuit, will produce an exact time scaling of every other voltage and current in the system. Except for the time-scale factor, the new system will perform exactly k times more (or less) rapidly than the old.

Often a circuit includes time-varying impedances, like the totem-pole switching elements within a digital driver circuit. In this case a time dilation (or compression) of the independent driving functions for all the impedance variations, in conjunction with time scaling of all the other reactive elements in the circuit, will produce the same general time-scaling result. This is the form in which the time-scaling principle is most important within the realm of digital systems work.

To scale a transmission line in time you must modify the total transmission-line inductance and capacitance by a factor of k meaning that the length of every transmission structure must be scaled by the factor k . Transmission-line impedance, being the square root of the ratio of inductance to capacitance, remains unchanged. Combining this requirement with the other ideas in this section, we arrive at a final statement of time scaling appropriate for use in digital systems work.

Beginning with a circuit composed of one or more digital drivers, some passive L, C, and R elements, and one or more transmission lines, you may scale the speed of operation by doing the following:

1. Scale lumped L and C components by the factor k ,
2. Lumped resistances remain fixed,
3. Scale the delay of all distributed transmission elements by the factor k ,
4. Transmission-line impedances remain fixed,
5. Scale all internal logic delays and timing specifications by the factor k ,
6. Scale the rise/fall times of all logic drivers by the factor k ,
7. Scale the timing for all external inputs by the factor k , and
8. Scale all clock intervals by the factor k .

The new circuit will behave identically to the first, but at a different scale of time (time t in the old circuit maps to time kt in the new).

The preceding rules apply to all circuits with deterministic inputs. There exist certain infinite-bandwidth random signals that cannot be so easily time-scaled. One example is white Gaussian noise. To see the difficulty, imagine white Gaussian noise applied to a low-pass filter. White noise goes in, and a random low-pass filtered signal comes out. In this circuit the output signal power is a function of the equivalent noise power bandwidth of the filter. If you scale the inductance and capacitance values within the filter by a constant k , the new bandwidth changes to 1/ k times the old bandwidth, and the output power changes to 1/ k times the old output power. That change of power violates the spirit of pure time scaling.

To rectify this situation, we are forced to conclude that the spectral power density of a white Gaussian noise signal should be scaled proportional to k . This problem is peculiar only to random signals with infinite bandwidth (and therefore infinite power). As soon as you specify a particular cutoff bandwidth for any random signal, you obtain a signal with finite total power. Consistent application of the scaling principle then requires that you scale the cutoff frequency of the noise signal proportional to 1/ k . Once the cutoff frequency is so scaled, you have in effect spread the same amount of power evenly over a bandwidth 1/ k times the original, so you should see k times the power density concentrated within each spectral interval (i.e., the spectral power density works out to the correct value). For an infinite-bandwidth white noise signal, you achieve this same result by scaling the spectral power density of the source.

The principle of time scaling for noise signals points out that without modification of the spectral power density of the white noise at the input to a circuit, a slower circuit always exhibits less noise in its output than a faster one. This is an immutable principle of high-frequency circuit design. It's the reason that FDDI optical transceivers can operate at 125 Mb/s with a greater receive sensitivity than Gigabit Ethernet optical transceivers working at 1250 Mb/s.

Example of time scaling

The shorter the risetime, the shorter the permissible length of unterminated transmission line stubs.

As promised earlier, let's now look in detail at how the time-scaling principle is used. I shall pick a simple example, involving a bus, four transceivers, and some connectors. There is one common clock used on the bus, driven from the center. Suppose you wish to increase the operating speed by a factor of four, and you want to maintain precisely the same signal fidelity as in the original bus. The pure time-scaling approach requires that you should first obtain faster drivers, with faster rise/fall times and shorter setup-hold requirements, all scaled to 1/4 their original values. That much seems obvious.

You shall also have to shrink the bus delay by a factor of four. Unfortunately, there are only two means of accomplishing this goal: Either shorten the bus by a factor of four or implement the bus with a better dielectric material having a lower value of r . If the bus is presently implemented in FR-4 material ( r = 4.5), the alternate option alone is not sufficient to achieve your goal of a 4:1 speedup . Some shortening of the bus structure will be required.

The parasitic effects of the connectors will have to be scaled as well. According to the physical scaling principle, this could be accomplished by shrinking the connector geometry. In practice, the geometry may already be too small to permit further shrinkage , so one is forced to procure more expensive connectors with various features built in to ameliorate the parasitic effects.

If you are successful at simultaneously shrinking all the bus parameters together, the new bus will perform precisely as the old, only four times faster. Should you fail to fully reduce one of the parameters, you will have to make up the shortfall by overscaling one of the other factors.

Terminating the bus relieves you of the problem of having to scale absolutely everything. A properly terminated bus can be sped up without requiring a shortening of the structure, hence the popularity of terminations. In this case the signal waveforms will not be precisely the same as in the old bus, but as long as the bus lines settle adequately, the system still works.

POINTS TO REMEMBER

• Shrinking every parameter of an unterminated structure speeds its settling time in direct proportion to the scale factor.
• Terminated structures circumvent the link between physical size and signal quality.

 

1.3.4 Impedance Scaling with Constant Voltage

From time to time, you will want to modify the impedance of a circuit. This happens when you change the widths of pcb traces or when you wish to reimplement a long-distance communication system on a different style of copper cabling.

It is possible to change the impedance of a circuit without disturbing the shape of its voltage or current waveforms. This is done by first changing the impedance of every element in the circuit, and then changing the voltage and current excitations to the system to stimulate it in a manner analogous to the original circuit. I say analogous rather than identical because in this situation it is not possible to completely preserve both current and voltage waveforms. Either the voltage waveforms or the current waveforms (or some combination of both) must be modified as part of this procedure. I describe next the most common form of impedance scalingimpedance scaling with constant voltage.

In the constant-voltage method, all voltages in the new system will remain as they were in the old system. All currents in the new system will be scaled by the factor 1/ k , as compared to their values in the old system.

This is accomplished by first scaling all the impedances in the system. For linear impedances, we simply multiply the impedance value by a factor of k . This means that each resistance must take on a value that is k times as great as in the original circuit. Each inductance must do the same. Each capacitance in the new circuit must be scaled to 1/ k times its original.

The procedure for constructing the new circuit is as follows :

1. Scale all resistances and inductances by the factor k ,
2. Scale all capacitances by the factor 1/ k , in order that their impedances, 1/(2 p fC ), should be k times as great,
3. Scale the impedance of all distributed transmission elements by the factor k (this is a consequence of rules 1 and 2),
4. Leave all independent voltage sources the same, and
5. Scale all independent current sources by the factor 1/ k .

The new circuit will behave identically to the first, but with all currents scaled by 1/ k . This change in current implies that every instantaneous power level in the new circuit will be 1/ k times the equivalent power in the old circuit. Changing the impedance can have a major impact on power consumption.

It is also possible to scale impedance while holding constant the currents. In this case the voltages scale with k , and power also scales with k . Since most digital logic operates with voltage-mode sources (that is, sources whose output impedance is much lower than the impedance of the receivers), the constant-voltage scaling law is the one most commonly used.

This rule as stated applies to all linear lumped-element circuits, whether they be time invariant or time varying. In a linear circuit the scaling of impedance does not affect the ratios of impedancesso no changes occur in circuit loss or signal fidelity throughout the system. For nonlinear circuits the situation is different. For a nonlinear system it is not easy to talk sensibly about an impedance ratio, because the dynamic impedance of a nonlinear element changes as a function of its bias current. For a nonlinear circuit to scale properly you would have to modify the I-V relation for every nonlinear device according to the law that every point i in the old relation is mapped to a new point i / k . In the case of many digital driver/receiver problems this condition is easily met simply by specifying a different size FET output cell , and the conclusions derived from the application of this principle are applicable ; that is, increasing all circuit impedances while weakening the drivers will directly reduce power consumption without affecting signal fidelity.

If you set k less than unity, you find that a lower-impedance source coupled to a lower-impedance transmission line can drive larger capacitive loads.

This rule applies to lumped or distributed circuits for which the impedances are under your direct control and may be scaled. This rule does not apply in any practical way to problems involving radiation into free space, like antennas, for which it is not physically possible to directly modify the impedances related to unchanging physical factors like the permittivity of free space or the magnetic permeability of free space m .

Example of impedance scaling

The lower the impedance of a transmission line, the more loads it can bear.

POINT TO REMEMBER

• A lower-impedance source coupled to a lower-impedance transmission line can drive larger capacitive loads.

 

1.3.5 Dielectric-Constant Scaling

Increasing the dielectric constant surrounding a circuit slows its operation and decreases its impedance. For circuits that are entirely embedded within a uniform, homogeneous, dielectric material, increasing the dielectric constant by a fixed factor k increases all circuit capacitances by precisely k . This has the effect of increasing all transmission-line delays by a factor of k and reducing all transmission-line impedances by a factor of 1/ k . Circuits partially surrounded by a high-dielectric-constant medium enjoy the same benefits, but to a lesser degree.

Certain circuits benefit from the slow-speed operation made possible by high-dielectric-constant circuit board materials. One prime example is a microwave resonator. An effective resonator may be formed from a section of pcb trace cut to a length of 1/4 wavelength. These sorts of resonant elements are commonly used for microwave oscillators , filters, couplers, and mixers. For resonator applications, the higher the dielectric constant of the material surrounding the resonator trace, the shorter that trace may be made. High-dielectric-constant materials therefore serve a useful miniaturization function in microwave circuits. In general, high-dielectric-constant substrate materials accentuate the distributed nature of pcb traces, causing them to exhibit transmission-line behavior at lower than normal frequencies.

Certain other circuits benefit from the lower impedance made possible by high-dielectric-constant insulating materials. The premier example is a bypass capacitor. The purpose of a bypass capacitor is to provide a low-impedance connection between power and ground. The higher the dielectric constant of the material used to separate its plates, the higher the capacitance and the lower its impedance (at all frequencies sufficiently far below the first series resonant frequency of the capacitor ). High-dielectric-constant materials are desirable between the plates of lumped-element bypass capacitors.

Finally, many circuits decidedly do not benefit from the use of high-dielectric-constant materials. Pcbs used for high-speed digital computers belong to this class of circuits. In the digital application, delay is your enemy, not your friend. Even between the solid power and ground planes of a digital design, high-dielectric-constant materials rarely help. Some mixed-signal designs and multichip module (MCM) designs force the use of a high-dielectric-constant substrate material, such as alumina ( r = 10). In those cases one usually implements narrower trace widths than would normally be the case with an FR-4 substrate ( r = 4.3) in order to counteract the impedance-lowering tendencies of the high dielectric constant.

The rule of dielectric scaling applies to any circuit for which all conducting surfaces are in intimate contact with, and totally embedded in, a uniform, homogeneous dielectric material. The term embedded means that all electric fields associated with the circuit fall entirely within the surrounding dielectric medium. This rule is particularly applicable to stripline traces, and it is a useful approximation for microstrip behavior. In the interior of a capacitor whose plate geometry is small enough to act as a lumped-element circuit the scaling rule applies. In the interior of a capacitor whose plate geometry is too large to act as a lumped-element circuit the rule still applies; however, the inductive effects associated with the distributed nature of the circuit may interfere with your ability to directly measure an increase in total capacitance proportional to k .

Example of dielectric scaling

All other things being equal, changing from an FR-4 substrate ( r = 4.3) to an Alumina substrate ( r = 10) increases the raw, unloaded pcb trace delay by 52% and lowers the trace impedance by 34%.

Changing to a lower dielectric constant will increase the characteristic impedance and decrease the delay. If you then broaden the line width to obtain the same characteristic impedance as in the original circuit you will find the skin effect losses are reduced.

1.3.5.1 Partially Embedded Transmission Lines

Many practical transmission-line structures lie only partially embedded within a dielectric material. For these lines the per-unit-length capacitance does not scale precisely with k . For example, imagine a stripline positioned very near the edge of a pcb. This stripline enjoys the benefits of a solid plane above and a solid plane below, confining most of the electric field energy surrounding the stripline to the dielectric medium between the planes. There are, however, some pathological paths for the electric fields that may be drawn, starting with the stripline, penetrating sideways through the dielectric medium to the outside air surrounding the board, and returning through the air to the planes on the top (or bottom) surface of the board. Obviously, these paths are not completely embedded within the dielectric medium. Some electric field energy will be stored along these paths, with the result that the effective electric permittivity experienced by the stripline will fall somewhat between the electric permittivity of the pcb dielectric medium and the electric permittivity of air. Air being the fastest dielectric medium known, you may conclude that a stripline positioned near the edge of a pcb will exhibit slightly higher impedance and slightly less delay than its more deeply embedded cousins. Its impedance and delay will also be somewhat less sensitive to variations in the dielectric material. Microstrip traces, because they lie on the outside surface of a pcb exposed on one side to air, exhibit this effect to an even greater degree. Striplines positioned well back into the interplane region, at least 20 h away from the edge of the planes (where h is the trace height above the nearest plane), perform for all practical (digital) purposes as completely embedded striplines.

POINT TO REMEMBER

• Reducing the dielectric constant of your transmission-line substrate increases the characteristic impedance and decreases the delay.

 

1.3.6 Magnetic Permeability Scaling

Increasing the magnetic permeability surrounding a circuit slows its operation and increases its impedance. For circuits that are entirely embedded within a uniform, homogeneous, permeable material, increasing the permeability by a fixed factor k increases all circuit inductance by precisely k . This has the effect of increasing all transmission-line delays by a factor of k and increasing all transmission-line impedances by a factor of k . Circuits partially surrounded by a highly permeable medium enjoy the same benefits but to a lesser degree.

This trick is used in the design of delay lines. One notable application appears in all analog color television receivers. Within the television receiver the luminance signal (the black-and-white information) has a bandwidth of approximately 6 MHz. Buried within that same band is a chroma signal. The chroma signal controls the relative intensities of the RGB electron guns. As received, the luminance and chroma signals are aligned in time. As these signals are processed inside the receiver, the chroma signal is extracted and decoded from the main signal by a set of filters having a bandwidth of approximately 500 KHz. These extraction filters delay the chroma information by roughly 500 ns relative to the luminance. A matching delay is then applied to the luminance signal to realign it with the chroma information prior to driving the RGB guns. The delay in older television sets was nothing more than a big, slow transmission line. It was typically implemented in the form of a wire helically wrapped around a long stick of material with high magnetic permeability. The highly permeable material slows the propagation time of the transmission line, thereby shrinking its physical length to a practical and manufacturable size. By whatever factor the delay is increased, so also goes the transmission-line impedance. This helps raise the impedance up into a range easily driven by analog tube circuits. (Use of a high-dielectric-permittivity material in this case would have lowered the impedance to an unusable extent).

Without the help of a highly permeable material, a comparable air-dielectric transmission line would have to be some 500 feet in length.

POINT TO REMEMBER

• Adjustments to magnetic permeability are rarely made in digital circuits.