Hierarchy of Regions

The transmission loss associated with any conductive transmission media increases monotonically with frequency. Sweeping from low frequencies to high, the slope of the loss curve changes in a predictable way as you pass the onset of various regions of operation. The progression of regions, and the transmission performance within each region, is the subject of this chapter.

Alternate forms of transmission structures exist, such as fiber- optic waveguides and various forms of RF waveguides, that cannot convey DC signals. In these alternate structures the loss function must be necessarily be nonmonotonic, leading to a different hierarchy of performance regions. The discussion of regions presented here applies only to conductive transmission structures as normally used in digital applications.

Figure 3.2 illustrates the general arrangement of performance regions pertaining to copper media. The particular data shown in this diagram represents a 150- m m (6-mil), 50- W FR-4 pcb stripline . The waveguide dispersion region for this trace begins at frequencies higher than shown on the chart.

Figure 3.2. Performance regions for a 150- m m (6-mil), 50- W , FR-4 stripline.

The distinguishing features of each region may be determined by analysis of the transmission-line propagation coefficient [3.13], propagation function [3.14], and characteristic impedance [3.15].

Equation 3.13

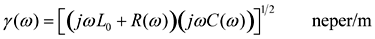
Equation 3.14

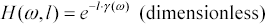
Equation 3.15

 

where	R ( w ), L , and C ( w ) represent the per-meter parameters of resistance, inductance, and capacitance respectively,
	the line conductance G is assumed zero, and
	the propagation function H at frequency w (rad/s) varies exponentially with the product of the length l and the propagation coefficient g .

Near DC the magnitude of the inductive reactance, w L dwindles to insignificance in comparison to the DC resistance. All that matters below this point is the relation between the DC resistance of the line and its capacitance. Lines at such low frequencies are said to operate in the RC region.

At higher frequencies the inductive reactance grows, eventually exceeding the magnitude of the DC resistance, forcing the line into the LC region.

Beyond the LC transition the internal inductance of the conductors (a mere fraction of the total inductance) becomes significant compared to the DC resistance. This development forces a redistribution of current within the bodies of the conductors. The redistribution of current heralds the arrival of the skin-effect region.

Dielectric losses are present at all frequencies, growing progressively more severe at higher frequencies. These losses become noticeable only when they rise to a level comparable with the resistive losses, a point after which the line is said to operate in the dielectric-loss-limited region.

At frequencies so high that the wavelength of the signals conveyed shrinks to a size comparable with the cross-sectional dimensions of the transmission line, other non-TEM modes of propagation appear. These modes do not by themselves portend a loss of signal power, but they can create objectionable phase distortion (i.e., dispersion of the rising and falling edges) that limits the maximum speed of operation. The region in which non-TEM modes must be taken into consideration is called the waveguide region.

At any frequency, regardless of the mode of operation, a transmission line can always be shortened to a length l LE ( w ) below which the line operates not in a distributed fashion, but in a mode reminiscent of a simple lumped-element circuit. The lumped-element region appears as a broad band underlying all the other regions in Figure 3.2, bounded by two dotted -line segments describing the function l LE ( w ).

As the length of a transmission line continues to shrink, at a point several orders of magnitude below l LE ( w ) it acts as a perfect wire.

POINTS TO REMEMBER

• Sweeping from low frequencies to high, the loss curve for a transmission line changes in a predictable way as you pass the onset of various regions of operation.
• The distinguishing features of each region are determined by the propagation coefficient, propagation function, and characteristic impedance.
• The regions usually appear in this order: lumped-element, RC, LC, skin-effect, dielectric, and waveguide.

 

3.2.1 A Transmission Line Is Always a Transmission Line

Article first published in EDN Magazine , April 4, 2002

Toss one end of a stout rope to a circus strongman. Then back up, pulling the rope taut as you go. When you are standing about 50 ft apart, flick the rope with a rapid up-and-down motion. If the man at the other end holds the line taut, you will observe a familiar pattern of wave propagation. Your up-and-down stroke first passes quickly from you to the strongman. At his end, the waveform reflects, sending an inverted copy of the original pulse back towards you. One round-trip delay after the initial flick, you feel the echo of your (attenuated and inverted) original excitation . Then, the residual signal bounces back and forth many times with an exponentially decaying amplitude.

 

 

This simple physical analogy reveals much about the behavior of pcb transmission lines. It shows propagation of the input signal, reflection at the far end, and residual ringing.

It also reveals a temporal disconnection between the ends of a long transmission line. In the example, your strongman stands so far away that the propagation delay across the taut rope easily exceeds the rise-and-fall time of your input signal. Under these conditions, when you first flick the rope, you feel only the mass and tautness of the rope, not the strongman.

Your interaction with the strongman proceeds in three stages. First, you interact with the rope. Then, the rope conveys your inputs of force and velocity to the load. Finally, your signal (now delayed and possibly attenuated) interacts with the load. This sequence corresponds precisely to the behavior of an electrical source, a transmission line, and its load ”provided that the delay of the line exceeds the rise (or fall) time of the source.

To expose the temporal disconnection in more interesting terms, suppose I drape a black curtain halfway between you and the strongman. With the curtain in place, as long as I don't change the tautness of the rope, you can't tell whether the rope is anchored to a man, a block of wood, or another long section of rope. Obviously, you can infer from the size and timing of the echo the characteristics of the far-end load, but before the echo returns, in the first moment after you create an outgoing waveform, you feel only the mass and tautness of the rope, not the anchor.

When you first flick a rope, you feel only the mass and tautness of the rope, not the anchor at the far end.

 

Electrical transmission lines exhibit precisely the same effect. The input impedance of a long transmission line, in the brief interval of time before the echo returns, depends only on the characteristics of the line itself, not on the load.

"But what," asks a student, "about a short transmission line? In that case, doesn't the driver see the load directly? Does the input impedance thus behave one way on a long transmission line but differently when the load is adjacent to the driver? How does it know what to do?"

To answer this question, I want you to walk over to your strongman and clench the rope right next to his hands. Pull hard. What you feel now is the strength of his grip, not the rope. At a short distance, no matter what kind of rope you use, thick or thin, the same result applies: You feel the strongman, not the rope.

Keep in mind that in both cases, the rope remains a rope. It doesn't suddenly change character. It still conveys your forces to the strongman, only it does so with such speed that the returning signal influences you instantaneously. Before you even begin to create part of a rising edge, the returning (and opposing) force holds the rope back down. The instantaneously returning forces, in contrast to the temporally disconnected reflections of the previous case, are responsible for the change in behavior.

Similarly, in the world of high-speed digital design, a pcb trace of any length always remains a transmission line. It supports two modes of propagation, going out to the load and back. When the line is short, these two modes of propagation still exist, only their temporal superposition creates the illusion of a direct connection between source and load.

POINTS TO REMEMBER

• A pcb trace of any length always remains a transmission line, supportig two modes of propagation (out and back).
• When a transmission line is short, two modes of propagation still exist, only their temporal superposition creates the illusion of a direct connection between source and load.