THE COMMUTATIVE PROPERTY OF LINEAR TIME-INVARIANT SYSTEMS
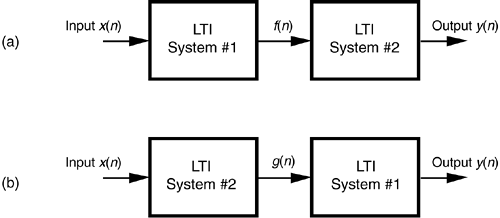
Although we don't substantiate this fact until we reach Section 6.8, it's not too early to realize that LTI systems have a useful commutative property by which their sequential order can be rearranged with no change in their final output. This situation is shown in Figure 1-10 where two different LTI systems are configured in series. Swapping the order of two cascaded systems does not alter the final output. Although the intermediate data sequences f(n) and g(n) will usually not be equal, the two pairs of LTI systems will have identical y(n) output sequences. This commutative characteristic comes in handy for designers of digital filters, as we'll see in Chapters 5 and 6.
Figure 1-10. Linear time-invariant (LTI) systems in series: (a) block diagram of two LTI systems; (b) swapping the order of the two systems does not change the resultant output y(n).
 |
Amazon |  |
