FREQUENCY-DOMAIN WINDOWING | Chapter Thirteen. Digital Signal Processing Tricks

There's an interesting technique for minimizing the calculations necessary to implement windowing of FFT input data to reduce spectral leakage. There are times when we need the FFT of unwindowed time domain data, while at the same time we also want the FFT of that same time-domain data with a window function applied. In this situation, we don't have to perform two separate FFTs. We can perform the FFT of the unwindowed data and then we can perform frequency-domain windowing on that FFT results to reduce leakage. Let's see how.

Recall from Section 3.9 that the expressions for the Hanning and the Hamming windows were wHan(n) = 0.5 –0.5cos(2pn/N) and wHam(n) = 0.54 –0.46cos(2pn/N), respectively. They both have the general cosine function form of

for n = 0, 1, 2, ..., N–1. Looking at the frequency response of the general cosine window function, using the definition of the DFT, the transform of Eq. (13-8) is

Equation 13-9

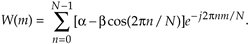
Because 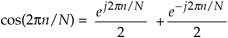, Eq. (13-9) can be written as

Equation 13-10

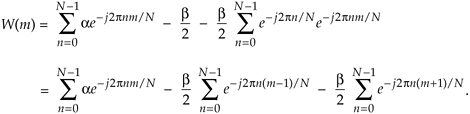
Equation (13-10) looks pretty complicated, but using the derivation from Section 3.13 for expressions like those summations we find that Eq. (13-10) merely results in the superposition of three sin(x)/x functions in the frequency domain. Their amplitudes are shown in Figure 13-10.

Figure 13-10. General cosine window frequency response amplitude.

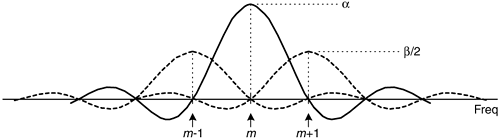
Notice that the two translated sin(x)/x functions have side lobes with opposite phase from that of the center sin(x)/x function. This means that a times the mth bin output, minus b/2 times the (m–1)th bin output, minus b/2 times the (m+1)th bin output will minimize the sidelobes of the mth bin. This frequency domain convolution process is equivalent to multiplying the input time data sequence by the N-valued window function w(n) in Eq. (13-8)[12–14].

For example, let's say the output of the mth FFT bin is X(m) = am + jbm, and the outputs of its two neighboring bins are X(m–1) = a–1 + jb–1 and X(m+1) = a+1 + jb+1. Then frequency-domain windowing for the mth bin of the unwindowed X(m) is as follows:

Equation 13-11

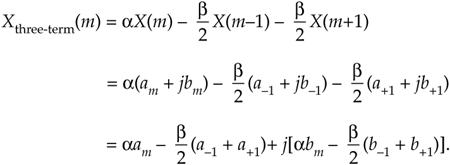
To compute a windowed N-point FFT, Xthree-term(m), we can apply Eq. (13-11), requiring 4N additions and 3N multiplications, to the unwindowed N-point FFT result X(m) and avoid having to perform the N multiplications of time domain windowing and a second FFT with its Nlog2(N) additions and 2Nlog2(N) multiplications. (In this case, we called our windowed results Xthree-term(m) because we're performing a convolution of a three-term W(m) sequence with the X(m) sequence.)

The neat situation here are the frequency-domain coefficients values, a and b, for the Hanning window. They're both 0.5, and the multiplications in Eq. (13-11) can be performed in hardware with two binary right shifts by a single bit for a = 0.5 and two shifts for each of the two b/2 = 0.25 factors, for a total of six binary shifts. If a gain of four is acceptable, we can get away with only two left shifts (one for the real and one for the imaginary parts of X(m)) using

Equation 13-12

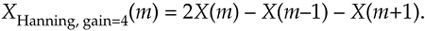
In application specific integrated circuit (ASIC) and field-programmable gate array (FPGA) hardware implementations, where multiplies are to be avoided, the binary shifts can be eliminated through hard-wired data routing. Thus only additions are necessary to implement frequency-domain Hanning windowing. The issues we need to consider are which window function is best for the application, and the efficiency of available hardware in performing the frequency domain multiplications. Frequency-domain Hamming windowing can be implemented but, unfortunately, not with simple binary shifts.

Along with the Hanning and Hamming windows, Reference [14] describes a family of windows known as Blackman windows that provide further FFT spectral leakage reduction when performing frequency-domain windowing. (Note: Reference [14] reportedly has two typographical errors in the 4-Term (–74 dB) window coefficients column on its page 65. Reference [15] specifies those coefficients to be 0.40217, 0.49703, 0.09892, and 0.00188.) Blackman windows have five non-zero frequency-domain coefficients, and their use requires the following five-term convolution:

Equation 13-13

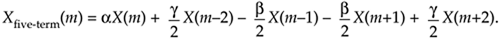
Table 13-3 provides the frequency-domain coefficients for several common window functions.

Let's end our discussion of the frequency-domain windowing trick by saying this scheme can be efficient because we don't have to window the entire set of FFT data; windowing need only be performed on those FFT bin outputs of interest to us. An application of frequency-domain windowing is presented in Section 13.18.

Table 13-3. Frequency-Domain windowing coefficients

Window function	a	b	g
Rectangular	1.0	—	—
Hanning	0.5	0.5	—
Hamming	0.54	0.46	—
Blackman	0.42	0.5	0.08
Exact Blackman	7938	9240	1430
	18608	18608	18608
3-term Blackman-Harris	0.42323	0.49755	0.07922