BINARY NUMBER PRECISION AND DYNAMIC RANGE | Chapter Twelve. Digital Data Formats and Their Effects

As we implied earlier, for any binary number format, the number of bits in a data word is a key consideration. The more bits used in the word, the better the resolution of the number, and the larger the maximum value that can be represented.[] Assuming that a binary word represents the amplitude of a signal, digital signal processing practitioners find it useful to quantify the dynamic range of various binary number schemes. For a signed integer binary word length of b+1 bits (one sign bit and b magnitude bits), the dynamic range in decibels is defined by

[] Some computers use 64-bit words. Now, 264 is approximately equal to 1.8 · 1019—that's a pretty large number. So large, in fact, that if we started incrementing a 64-bit counter once per second at the beginning of the universe (20 billion years ago), the most significant four bits of this counter would still be all zeros today.

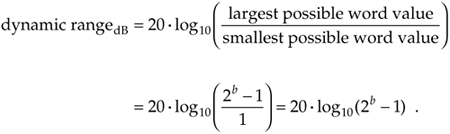
When 2b is much larger than 1, we can ignore the –1 in Eq. (12-6) and state that

Equation 12-6'

Equation (12-6'), dimensioned in dB, tells us that the dynamic range of our number system is directly proportional to the word length. Thus, an eight-bit two's complement word, with seven bits available to represent signal magnitude, has a dynamic range of 6.02 · 7 = 42.14 dB. Most people simplify Eq. (12-6') by using the rule of thumb that the dynamic range is equal to "six dB per bit."

URL http://proquest.safaribooksonline.com/0131089897/ch12lev1sec2