SHARPENED FIR FILTERS
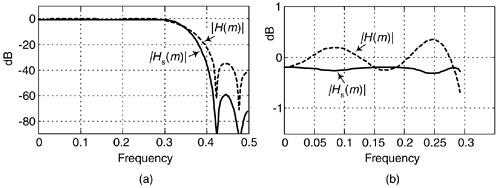
Here's an interesting technique for improving the stopband attenuation of a digital under the condition that we're unable, for whatever reason, to modify that filter's coefficients. Actually, we can a filter's double stopband attenuation by cascading the filter with itself. This works, as shown in Figure 13-32(a), where the frequency magnitude response of a single filter is a dashed curve |H(m)| and the response of the filter cascaded with itself is represented by solid curve |H2(m)|. The problem with this simple cascade idea is that it also doubles the passband peak-to-peak ripple as shown in Figure 13-32(b). The frequency axis in Figure 13-32 is normalized such that a value of 0.5 represents half the signal sample rate.
Figure 13-32. Frequency magnitude responses of a single filter and that filter cascaded with itself: (a) full response; (b) passband detail.

Well, there's a better scheme for improving the stopband attenuation performance of a filter and avoiding passband ripple degradation without actually changing the filter's coefficients. The technique is called filter sharpening[34], and is shown as Hs in Figure 13-33.
Figure 13-33. Filter sharpening process.
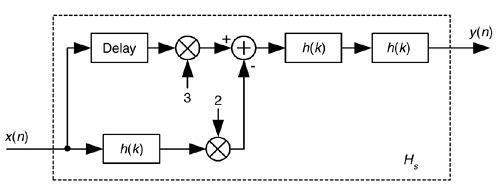
The delay element in Figure 13-33 is equal to (N–1)/2 samples where N is the number of h(k) coefficients, the unit-impulse response length, in the original H(m) FIR filter. Using the sharpening process results in the improved |Hs(m)| filter performance shown as the solid curve in Figure 13-34, where we see the increased stopband attenuation and reduced passband ripple beyond that afforded by the original H(m) filter. Because of the delayed time-alignment constraint, filter sharpening is not applicable to filters having non-constant group delay, such as minimum-phase FIR filters or IIR filters.
Figure 13-34. |H(m)| and |Hs(m)| performance: (a) full frequency response; (b) passband detail.
If perhaps more stopband attenuation is needed then the process shown in Figure 13-35 can be used, where again the delay element is equal to (N–1)/2 samples.
Figure 13-35. Improved filter sharpening FIR process.
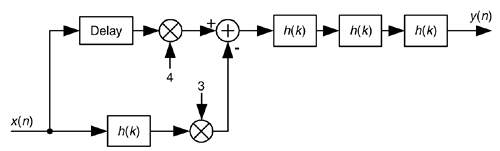
The filter sharpening procedure is straightforward and applicable to lowpass, bandpass, and highpass FIR filters having symmetrical coefficients and an odd number of taps. Filter sharpening can be used whenever a given filter response cannot be modified, such as an unchangeable software subroutine, and can even be applied to cascaded integrator-comb (CIC) filters to flatten their passband responses, as well as FIR fixed-point multiplierless filters where the coefficients are constrained to be powers of two[35,36].
 |
Amazon |  |
