EFFICIENT POLYNOMIAL EVALUATION
On the off chance that you didn't know, to speed up polynomial evaluations (computations) in software it's smart to use what's known as Horner's rule. An example of polynomial evaluation is, say, using the following expression to compute the arctangent of x:
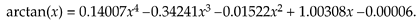
To see how the computational workload of polynomial evaluations can be reduced, consider the following kth-order polynomial:
Equation 13-126
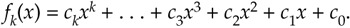
It can be rewritten as:
Equation 13-127
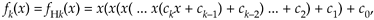
where the H subscript means Horner. Using this method to compute polynomials:
- reduces the number of necessary multiply operations, and
- is straightforward to implement using programmable DSP chips with their multiply and accumulate (MAC) architectures.
For example, consider the fifth-order polynomial:
Equation 13-128
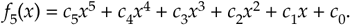
Evaluated in the standard way, Eq. (13-128) would require nine multiplies and five additions, whereas the Horner version
Equation 13-129
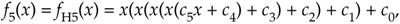
requires only five multiplies and five adds when the computations begin with the innermost multiply and add operations (c5x + c4).
Here are a few examples of polynomials in the Horner format:
Equation 13-130
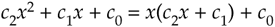
Equation 13-131
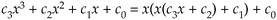
Equation 13-132
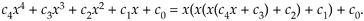
By the way, the multiplications and additions cannot be performed in parallel. Because Horner's rule is inherently serial, we need the result of the last multiplication before we can start the next addition, and that addition result is needed before the follow-on multiplication.
Horner's rule is another of those handy computer techniques we use whose origins are very old. Chinese mathematicians described it in the 1200s. European mathematicians (including William Horner) rediscovered and publicized it in the early 1800s. It seems Sir Isaac Newton also invented and used it in the 1600s.
URL http://proquest.safaribooksonline.com/0131089897/ch13lev1sec26
 |
Amazon |  |
