Section A.1. GRAPHICAL REPRESENTATION OF REAL AND COMPLEX NUMBERS | Appendix A. The Arithmetic of Complex Numbers

Table of contents:

A 1 GRAPHICAL REPRESENTATION OF REAL AND COMPLEX NUMBERS

A 1 GRAPHICAL REPRESENTATION OF REAL AND COMPLEX NUMBERS

To get started, real numbers are those positive or negative numbers we're used to thinking about in our daily lives. Examples of real numbers are 0.3, –2.2, 5.1, etc. Keeping this in mind, we see how a real number can be represented by a point on a one-dimensional axis, called the real axis, as shown in Figure A-1.

Figure A-1. The representation of a real number as a point on the one-dimensional real axis.

We can, in fact, consider that all real numbers correspond to all of the points on the real axis line on a one-to-one basis.

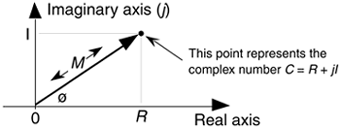
A complex number, unlike a real number, has two parts: a real part and an imaginary part. Just as a real number can be considered to be a point on the one-dimensional real axis, a complex number can be treated as a point on a complex plane as shown in Figure A-2. We'll use this geometrical concept to help us understand the arithmetic of complex numbers.[]

[] The complex plane representation of a complex number is sometimes called an Argand diagram—named after the French mathematician Jean Robert Argand (1768–1825).

Figure A-2. The phasor representation of the complex number C = R + jI on the complex plane.