AUTOMATIC GAIN CONTROL (AGC)
Since the early days of vacuum tube radios, circuits were needed to automatically adjust a receiver's gain, as an input signal varied in amplitude, to maintain a (relatively) constant output signal level. These feedback mechanisms, called automatic gain control (AGC) circuits, are an important component of modern analog and digital communications receivers. Figure 13-76(a) illustrates a simple digital AGC process[74,75]. Its operation is straightforward: the output signal power is sampled and compared to a reference level R (the desired output amplitude rms level). If the output signal level is too high (low), a negative (positive) signal is fed back reducing (increasing) the gain. The control parameter a regulates the amplitude of the feedback signal and is used to control the AGC's time constant (how rapidly gain changes take effect).
Figure 13-76. AGC process: (a) linear AGC circuit; (b) example input x(n) with amplitude fluctuations; (c) y(n) output for a = 0.01 and R = 1.
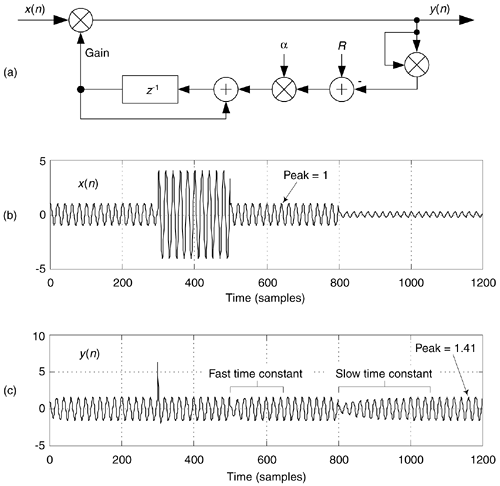
Given an input signal x(n) in Figure 13-76(b) whose amplitude envelope is fluctuating, the AGC structure provides the relatively constant amplitude y(n) output shown in Figure 13-76(c).
We called Figure 13-76(a) a "simple AGC process," but AGC is not all that simple. The process is a nonlinear, time-varying, signal-dependent, feedback system. As such it's highly resistant to normal time-domain or z-domain analysis. This is why AGC analysis is empirical rather than mathematical, and explains why there's so little discussion of AGC in the DSP literature.
Depending on the nature of x(n), the feedback signal may fluctuate rapidly and the feedback loop will attempt to adjust the system gain too often. This will cause a mild AM modulation effect inducing low-level harmonics in the y(n) output. That problem can be minimized by inserting a simple lowpass filter in the feedback loop just before, or just after, the R adder. But such filtering does not remedy the circuit's main drawback. The time constant (attack time) of this AGC scheme is input signal level dependent, and is different depending on whether the x(n) is increasing or decreasing. These properties drastically reduce our desired control over the system's time constant. To solve this problem, we follow the lead of venerable radio AGC designs and enter the logarithmic domain.
We can obtain complete control of the AGC's time constant, and increase our AGC's dynamic range, by using logarithms as shown in Figure 13-77(a). As is typical in practice, this log AGC process has a lowpass filter (LPF) to eliminate too-rapid gain changes[76]. That filter can be a simple moving average filter, a cascaded integrator-comb (CIC) filter, or a more traditional lowpass filter having a sin(x)x impulse response.
Figure 13-77. AGC process: (a) logarithmic AGC circuit; (c) y(n) output for a = 0.01 and R = 1.
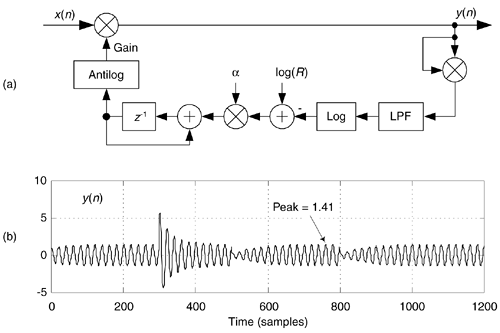
For the logarithmic AGC scheme, the feedback loop's time constant is dependent solely on a and independent of the input signal level, as can be seen in Figure 13-77(b) when the x(n) input is that in Figure 13-76(b). The Log and Antilog operations can be implemented as log2(x) and 2x, respectively.
 |
Amazon |  |
