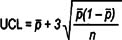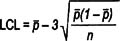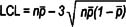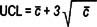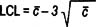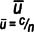Variation Analysis

Overview

Purpose of these tools

• To separate special cause from common cause variation
• To detect trends and patterns in data that provide clues about the sources of variation (with the ultimate goal of reducing or eliminating those sources)

Deciding which tool to use

This section features two types of tools used to understand variation:

1. Time series charts, on which you plot data in the order of their occurrence
2. Capability calculations, which compare the range of actual process output against the range (specifications or tolerance) that meet customer requirements

When collecting process data, plot the data on one of the following charts before continuing with other analyses:

1. Time series plots (also called run charts): Simple charts of process data that require calculation only of a median (see p. 119). Easy to do "in the field" for up to 50 data points with just a pencil and paper.
   • Use the run chart table (p. 121) to identify patterns associated with special cause variation
2. Control charts: Time series plots that have the added features of a centerline (the mean) and control limits, calculated from the data, which show the expected range of variation in the process (usually ± 3 standard deviations from the mean). These are a bit more complicated than time series plots because additional calculations are required. However, they are better at detecting several kinds of special cause variation.
   • Different kinds of data require different formulas for calculating the centerline and control limits. See p. 123 for instructions on how to select the right set of calculations.
   • Use the tests for special cause variation (p. 133) for identifying patterns that indicate the presence of special cause variation.

Review of variation concepts

Variation is the term applied to any differences that occur in products, services, and processes. There are two types of variation:

1. Common cause—the variation due to random shifts in factors that are always present in the process.
   • A process with only common cause variation is said to be "in control" (or "in statistical control").
   • Though random, the variation will be stable and predictable with a determined range
   • An "in control" process may still be unacceptable because it has too much variation—meaning the output can be unacceptable to the customer and/or can incur too many internal costs.
   • The only way to reduce common cause variation is by fundamentally changing the system—redesigning the process so a different mix of factors affects the output.
2. Special cause (also called "assignable" cause variation)—variation above and beyond common cause variation, arising from factors that are not always present in the process.
   • Every process has common cause variation. One that ALSO has special cause variation is said to be out of control.
   • Variation from special causes is not random (that is, it generates identifiable patterns)—but you can't predict when it will appear or what its impact will be (so is unstable and unpredictable).
   • Reduce special cause variation by tracking down and eliminating the specific, assignable root cause(s), looking for "what's different" in the process when the special cause variation appears.

Note that there are different strategies for dealing with the two types of variation: To reduce common cause variation, you have develop new methods for doing the work everyday. To eliminate special cause variation, you have to look for something that was temporary or that has changed in the process, and find ways to prevent that cause from affecting the process again.

Time series plots (Run charts)

Purpose

• To show data points in the order in which they occurred
• To show if the process is changing over time

When to use time series plots

• Easy to construct, even by hand, and require fewer data points than control charts, so often used in the field to get an immediate sense of process performance (though you can also go immediately to control charts if you have easy access to statistical software for data analysis)
• Easy to interpret using some basic guidelines, so used to detect trends and significant changes in the underlying process generating the data

How to create and use time series plots

1. Collect data and be sure to track the order in which the data were generated by the process.
2. Mark off the data units on the vertical (y) axis and mark the sequence (1, 2, 3…) or time unit (11 Mar, 12 Mar, 13 Mar…) on the horizontal (X) axis.
3. Plot the data points on the chart and draw a line connecting them in sequence.

OPTIONAL: If you have done a histogram or have reason to believe the data are from a normal distribution (see p. 114), you can use the Run Chart Table (p. 121) to look for patterns of special causes. If this is the case…

1. Determine the median (see p. 107) and draw a line at that value on the chart.

   

2. Count the number of points not on the median.
3. Circle then count the number of runs.
   • A "run" is defined as series of consecutive points that do not cross the median
   • Points on the median are not counted toward total points
   • Points on the median do not interrupt the run if the median is not crossed (see points 11 to 15 in the example below)

     

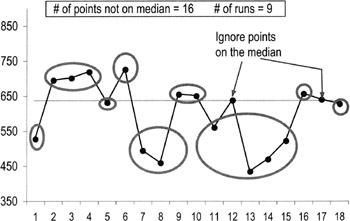
4. Use the Run Chart Table (next page) to interpret the results.
   • The table gives you a range of runs you can expect to see if the data are random (common cause variation only) and from a normal distribution.
   • If the number of counted runs is bigger or smaller than expected, you may have special cause variation in the process or the data are not normal.
     • Plot the points on a histogram to look at the distribution
     • Look to see what was different or what changed in the process during the time those data points were collected to discover the source of special cause variation

Run chart table

# pts not on median	Lower limit of runs	Upper limit of runs
10	3	8
11	3	9
12	3	10
13	4	10
14	4	11
15	4	12
16	6	12
17	5	13
18	6	13
19	6	14
20	6	14
21	7	15
22	7	16
23	8	16
24	8	17
25	9	17
26	9	18
27	9	19
28	10	19
29	10	20
30	11	20
31	11	21
32	11	22
33	11	22
34	12	23
35	19	23
36	13	23
37	13	25
38	14	25
39	14	26
40	15	26
41	16	26
42	16	27
43	17	27
44	17	28
45	17	29
46	17	30
47	18	30
48	18	31
49	19	31
50	19	32
60	24	37
70	28	43
80	33	48
90	37	54
100	42	59
110	46	65
120	48	70

Control chart basics

Highlights

• Control charts are similar to run charts in that they display measurement data in time order
• Additional lines help you identify special cause variation
  • The average (mean) is used for the centerline (instead of the median, used on a run chart).

    

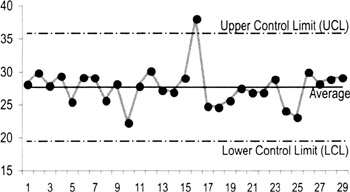
  • Control limits are added, representing the range of expected variation.
  • The control limits are ± 3 standard deviations off of the average (99.7% of the points in a set of normally distributed data will fall between the limits).
  • Control limits are not specification limits. Control limits are based on data and tell you how a process is actually performing. Spec limits are based on customer requirements and tell you how you want a process to perform.

Uses for control charts

• Establishing a measurement baseline
• Detecting special cause variation
• Ensuring process stability and enabling predictability
• Monitoring process over time
• Confirming the impact of process improvement activities

Data requirements

• Minimum of 25 consecutive subgroups, or
• Minimum of 100 consecutive observations
• Must be in time series order

Selecting a control chart

Fixed opportunity: the sample size or "unit" being sampled is constant Variable opportunity: the sample size or "unit" being sampled changes

If you aren't sure what kind of data you have, see p. 70.

See below for more details on selecting charts for continuous data and see p. 130 for selecting charts for attribute data.

Control charts for continuous data

In most cases, you will be creating two charts for each set of continuous data. The first chart shows the actual data points or averages, the second chart shows the ranges or standard deviations. Why use both?

The data (I or Xbar) chart…

• Shows changes in the average value of the process
• Is a visualization of the longer-term variation
• For an Xbar chart the key question: "Is the variation between the averages of the subgroups more than that predicted by the variation within the subgroups?"

The range (mR or R) chart…

• Reflects short-term variation
• The R-charts used with Xbar charts depict the ranges within subgroups of data; the key question: "Is the variation within subgroups consistent?"
• Range charts must be "in control" before we can build or use the I or Xbar charts

  

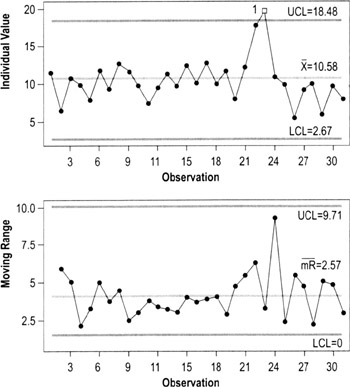
Selecting a control chart for continuous data

ImR chart (Individuals, moving Range)

Plots individuals data (I) on one chart and moving ranges (mR— the differences between each two adjacent points) on a second chart. Use when the best subgroup size is one, which will happen when…

• There are very few units produced (= low output rate) relative to how often process variables (sources of variation) may change
• There is little choice due to data scarcity
• A process drifts over time and needs to be monitored
• Sampling is very expensive or involves destructive testing

ImR is a good chart to start with when evaluating continuous data. You can often do a quick chart by hand then use it to build a different or more elaborate chart later.

X, R chart (Xbar&R, Average + Range)

Plots averages of subgroups (Xbar) on one chart and the ranges (R) within the subgroups on the other chart. The Xbar&R Chart is used with a sampling plan to monitor repetitive processes.

• Subgroup sizes typically range from 3 to 9 items. Frequently, practitioners will choose subgroups of 5
• All of the Tests for Special Causes (p. 133) can be applied with these charts
• The Xbar chart will highlight changes to the average ("between subgroups" or process accuracy)
• The R-chart will detect changes to "within subgroup" dispersion (process precision)

The Xbar&R chart is the most commonly used control chart because it uses the Central Limit Theorem (p. 114) to normalize data—meaning it doesn't matter as much what the underlying distribution of the data is. It is also more sensitive than the ImR to process shifts.

X,S chart (Xbar&S, Average + Standard Deviation)

Plots subgroup averages (Xbar) plus standard deviations of the subgroups (S). Similar in use to Xbar&R charts except these can be used only when you have sample sizes of at least 10 units (statisticians believe that the standard deviation is reliable only when sample sizes are 9 or larger). It's far more common to use smaller sample sizes (≤9) so in most cases an Xbar&R chart will be a better choice.

See below for instructions on rational subgrouping for Xbar&R and Xbar&S charts.

Subgrouping for continuous data

For both Xbar&R and Xbar&S charts, you'll need to collect data in sets of points called subgroups, then calculate and plot the averages for those subgroups. Rational subgrouping is the process of selecting a subgroup based upon "logical" grouping criteria or statistical considerations.

Often, you can use natural breakpoints to determine subgroups:

Ex: If you have 3 shifts operating per day, collect 1 data point per shift and calculate the average for those 3 data points (you'll plot one "average" reading per day)

Or if you want to look for differences between shifts, collect, say, 5 data points per shift (you'll plot 3 average readings every day, 1 per shift)

If the data are not normally distributed, use the guidelines on the Central Limit Theorem, p. 114, and rational subgrouping guidelines to determine the proper subgroup size.

Subgroup size selection can also be used to address the following data problems:

1. Trends and patterns—Use subgrouping to "average out" special cause patterns caused by logical grouping or time cycles.
   • A predictable difference in size from different injection mold diameters grouped together into one shot
   • A predictable difference in the output of 3 shifts grouped into 1 day
   • A predictable difference in incoming calls per day (M-F) grouped into 1 week
2. Too much data—Sometimes it is necessary to use subgrouping to reduce the number of data points plotted on a chart, which can make it easier to spot trends and other types of special cause variation.

Tips 

• Always try to convert attribute (discrete) data to continuous data and use Xbar&R or ImR charts. Convert attribute data to length, area, volume, etc.
• For data that occur infrequently (such as safety accidents), use the time between incidents (a continuous measure) rather than binomial attribute data (yes/no did an incident occur). Add a measure for leading indicators (such as days between near misses).

Control limit formulas for continuous data

The constants in these formulas will change as the subgroup size changes (see second table on next page).

Individuals + Moving Range Charts (ImR chart)
Centerline	X Average of data points	mR Average of the moving ranges
UCL	X + 2.66 mR	D4R
LCL	X − 2.66 mR	D3R

Subgroup Averages + Range (X&R chart)
Centerline	X Average of subgroup averages	R Average of subgroup ranges
UCL	X + A2R	D 4R
LCL	X 2 − A2R	D 3R

Subgroup Averages + Std Dev (X&S chart)
Centerline	X Average of subgroup averages	S Average of subgroup std. dev.
UCL	X + A3R	B4S
LCL	X − A3R	B3S

Note 

The X, R, and S symbols should technically be in lower-case letters, but (except for statistics books) are more often seen with capitals, so that is the convention used here. The A, D, and B factors are on the next page.

Factors for Control Chart Formulas

n	A2	A3	B3	B4	d2	D3	D4
2	1.88	2.66	.00	3.27	1.13	.00	3.27
3	1.02	1.95	.00	2.57	1.69	.00	2.57
4	.73	1.63	.00	2.27	2.06	.00	2.28
5	.58	1.43	.00	2.09	2.33	.00	2.11
6	.48	1.29	.03	1.97	2.53	.00	2.00
7	.42	1.18	.12	1.88	2.70	.08	1.92
8	.37	1.10	.19	1.82	2.85	.14	1.86
9	.34	1.03	.24	1.76	2.97	.18	1.82
10	.31	.98	.28	1.72	3.08	.22	1.78
11	.29	.93	.32	1.68	3.17	.26	1.74
12	.27	.89	.35	1.65	3.26	.28	1.72
13	.25	.85	.38	1.62	3.34	.31	1.69
14	.24	.82	.41	1.59	3.41	.33	1.67
15	.22	.79	.43	1.57	3.47	.35	1.65
16	.21	.76	.45	1.55	3.53	.36	1.64
17	.20	.74	.47	1.53	3.59	.38	1.62
18	.19	.72	.48	1.52	3.64	.39	1.61
19	.19	.70	.50	1.50	3.69	.40	1.60
20	.18	.68	.51	1.49	3.74	.42	1.59

Creating an ImR Chart

1. Determine sampling plan
2. Take a sample at each specified time or production interval
3. Calculate the moving ranges for the sample
   • To calculate each moving range, subtract each measurement from the previous one
     • Ex: subtract Observation 2 from Observation 1; or Observation 15 from Observation 14)
     • Treat all ranges as positive even if the difference is negative. (Ex: 10 − 15 = −5 but is recorded as a range of +5)
   • There will be no moving range for the first observation on the chart (because no data value preceded it)
4. Plot the data (the original data values on one chart and the and moving ranges on another)
5. After 20 or more sets of measurements, calculate control limits for moving Range chart
6. If the Range chart is not in control, take appropriate action
7. If the Range chart is in control, calculate control limits for the Individuals chart
8. If the Individuals chart is not in control, take appropriate action

Creating X,R charts or X,S charts

1. Determine an appropriate subgroup size and sampling plan
2. Collect the samples at specified intervals of time or production
3. Calculate the mean and range (or standard deviation) for each subgroup
4. Plot the data. The subgroup means go on one chart and the subgroup ranges or standard deviations on another
5. After 20 or more sets of measurements, calculate control limits for the Range chart
6. If the Range chart is not in control, take appropriate action
7. If the Range chart is in control, calculate control limits for the Xbar chart
8. If the Xbar chart is not in control, take appropriate action

Control charts for attribute data

• Review the definition of data types on p. 70
• Attribute control charts are similar to variables control charts except they plot proportion or count data rather than variable measurements
• Attribute control charts have only one chart which tracks proportions or counts over time (there is no range chart or standard deviation chart like there is with continuous data)

Binomial data

When data points can have only one of two values—such as when comparing a product or service to a standard and classifying it as being acceptable or not (pass/fail)—it is called binomial data. Use one of the following control charts for binomial data:

p-chart: Charts the proportion of defectives in each subgroup np-chart: Charts the number of defectives in each subgroup (must have same sample size each time)

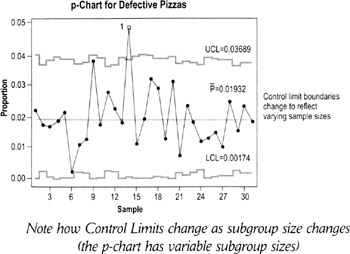
Note how Control Limits change as subgroup size changes (the p-chart has variable subgroup sizes)

P-charts are often used in transactional situations: billing errors, defective loan applications, proportion of invoices with errors, defective room service orders, sales order data, etc.

Poisson data

A Poisson (pronounced pwa-sahn) distribution describes count data where you can easily count the number of occurrence (Ex: errors on a form, dents on a car), but not the number of non-occurrences (there is no such thing as a "non-dent"). These data are best charted on either:

c-chart: Charts the defect count per sample (must have the same sample size each time)

u-chart: Charts the number of defects per unit sampled in each subgroup (uses a proportion, so it's OK if sample size varies)

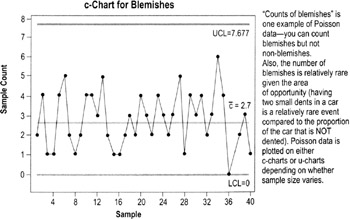
"Counts of blemishes" is one example of Poisson data—you can count blemishes but not non-blemishes. Also, the number of blemishes is relatively rare given the area of opportunity (having two small dents in a car is a relatively rare event compared to the proportion of the car that is NOT dented). Poisson data is plotted on either c-charts or u-charts depending on whether sample size varies.

If the sample size is always the same (10% variation in sample size is OK) use c-charts. If the sample size varies use the u-chart.

Tips for converting attribute data to continuous data 

In general, much more information is contained in continuous data than in attribute data, so control charts for continuous data are preferred. Possible alternatives to attribute charting for different situations:

Situation	Possible Solution
Infrequent failures	Plot time between failures on an ImR chart
Similar subgroup size	Plot the failure rate on an ImR chart

Creating p, np, c, and u charts

When charting continuous data, you normally create two charts, one for the data and one for ranges (ImR, Xbar&R, etc.). In contrast, charts for attribute data use only the chart of the count or percentage.

1. Determine an appropriate sampling plan
2. Collect the sample data: Take a set of readings at each specified interval of time
3. Calculate the relevant metric (n, np, c, or u)
4. Calculate the appropriate centerline
5. Plot the data
6. After 20 or more measurements, calculate control limits
7. If the chart is not in control, take appropriate action

Control limit formulas for attribute data

Chart Type	Centerline	Upper Control Limit	Lower Control Limit
p	p
np	np
c	c
u

Assumptions for interpreting control charts

The "test for special causes" described on the following pages assume that you have normally distributed data (see p. 114):

• Control limits are ± 3 standard deviations from the mean—and calculation of std. dev. assumes normal distribution
• If the distribution of the plotted points is not normal, the control limits cannot be used to detect out-of-control conditions such as outliers
  • To fix this problem, use the Central Limit Theorem (p. 114) to determine what subgroup sample sizes will allow you to plot data averages that are normally distributed

All tests for special causes also assume you have independent observations:

• Independence means the value of any given data point is not influenced by the value of any other data point
• If data are not independent, the data values will not be random
• This means the rules for determining special cause variation cannot be applied (because they are based on rules of statistical probability)

Interpreting control charts (Tests for Special Cause Variation)

Many of these tests relate to "zones," which mark off the standard deviations from the mean. Zone C is ± 1 std dev.; Zone B is between 1 and 2 std. dev.; and Zone A is between 2 and 3 std dev.

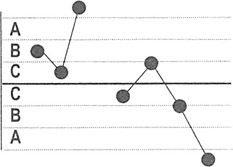
1 point beyond Zone A: Detects a shift in the mean, an increase in the standard deviation, or a single aberration in the process. Check your R-chart to rule out increases in variation.

9 points in a row on one side of the average in Zone C or beyond: Detects a shift in the process mean.

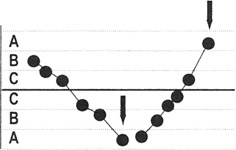
6 points in a row steadily increasing or decreasing: Detects a trend or drift in the process mean. Small trends will be signaled by this test before the first test.

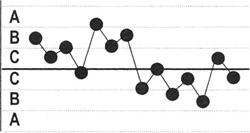
14 points in a row alternating up and down: Detects systematic effects, such as two alternately used machines, vendors, or operators.

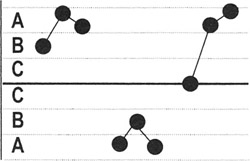
2 out of 3 points in a row in Zone A or beyond: Detects a shift in the process average or increase in the standard deviation. Any two out of three points provide a positive test.

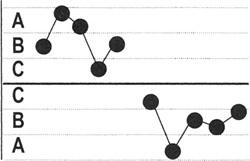
4 out of 5 points in Zone B or beyond: Detects a shift in the process mean. Any four out of five points provide a positive test.

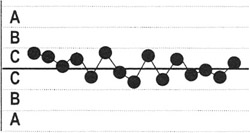
15 points in a row in Zone C, above and below the centerline: Detects stratification of subgroups—appears when observations in a subgroup come from sources with different means.

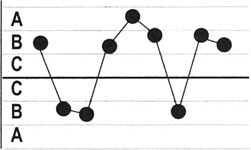
8 points in a row on both sides of the centerline with none in Zone C: Detects stratification of subgroups when the observations in one subgroup come from a single source, but subgroups come from different sources with different means.

Background on process capability calculations

Purpose

To compare the actual variation in a process (Voice of the Process) to its allowed variation limits (Voice of the Customer):

• The Voice of the Process is reflected in the control limits
• The Voice of the Customer is reflected in process specifications

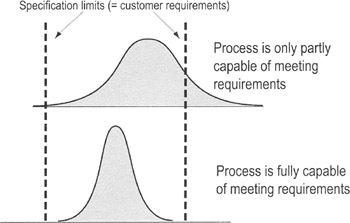
The proportion of current values that fall inside specification limits tells us whether the process is capable of meeting customer expectations.

When to use process capability calculations

Can be done on any process that has a specification established, whether manufacturing or transactional, and that has a capable measuring system. More specifically, in manufacturing and engineering…

• Performed on new equipment as part of the qualification and approval process
• Performed on existing processes to establish a baseline of current operations
• Performed on a pilot process prior to widespread rollout to prove actual performance capability meets or exceeds required performance
• Done periodically to monitor wear and tear on equipment, and deterioration of a process for whatever reason (material, personnel, environment, etc.)

In services…

• Performed on a pilot process prior to widespread rollout to prove actual performance capability meets or exceeds required performance
• Performed periodically to assure that performance standards are maintained or to highlight the need to reinforce existing standards
• Performed whenever outside or inside factors change, to prove the process is still capable of delivering high-quality, timely service

Tip 

• Because capability indices are "unitless" (not associated with a unit like inches, minutes, etc.), you can use capability statistics to compare the capability of one process to another

Prework for Capability Analysis

When beginning to measure/monitor a parameter always:

• Calibrate measuring system (unless done recently)
• Perform Measuring System Analysis (MSA)
  • See p. 87 for Gage R&R for continuous data
  • See p. 100 for MSA for discrete/attribute data
• Ensure the process is in statistical control
• Confirm customer requirements to establish specification limits
• Requirements are the same as for control charts:
  • Minimum of 25 consecutive subgroups (representing a minimum of 100 observations) or individual data points
  • Must be in time series

Confusion in short term vs long term process capability calculations

Any process experiences more variation in the long term than in the short term, so "capability" will vary depending on whether you're collecting data for a short period of time (a day, week) or for much longer (several months or years).

• For practical purposes, "long term" means data have been collected over a long enough period that you believe it likely that you've seen 80% of the process variation

The equations and basic concepts are identical for calculating short-term and long-term capability except for how the standard deviation is calculated:

• In the C metrics, the standard deviation is calculated from the subgroups and therefore represents short-term variation (which means C metrics represent short-term capability)
• In the P metrics, the standard deviation is calculated from all the data, and therefore represents long-term variation, and P metrics represent long-term capability

Be alert: Many companies calculate process capability statistics using long-term variation, but use the "C" labels; others are careful to distinguish between long—and short-term variation. Check with data experts in your company to see what standards they follow.

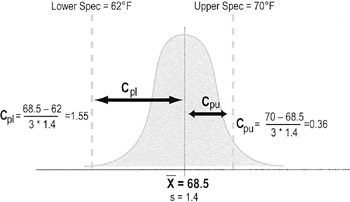
Calculating process capability

Note 

The calculations here are for continuous, normal data. Refer to any good statistics textbook for capability analysis on attribute data.

The choice: Cp vs. Cpk (or "P" versions)

• Cp and Pp calculations represent an overall comparison of process output vs. desired limits. These calculations are based on the full range of variation compared to specification (they don't compare performance to a mean), so are best used when:
  • The mean can easily be adjusted (such as transactional processes where resources can easily be added with no or minor impact on quality) AND
  • The mean is monitored (so process owner will know when adjustment is necessary—doing control charting is one way of monitoring)
• Cpk and Ppk calculations build on comparisons of variation against the upper and lower specification limits separately. The calculations include the mean, so are best used when the mean is not easily adjusted.
  • For process improvement efforts, you will most likely use Ppk because it is most representative of what the customer experiences over time
  • Cpl and Cpu (and P versions) are intermediate steps for determining Cpk

Calculating and interpreting Cp or Pp

Cp and Pp are ratios of total variation allowed by the specification to the total variation actually measured from the process.

• Formulas are the same for Pp except "normal variation" is calculated from long-term process variation
• If Cp < 1 then the variability of the process is greater than the size of the specification range
• Typical goals for Cp are greater than 1.33 (or 1.67 for mission critical/safety items)

Calculating and interpreting Cpk or Ppk

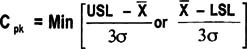
Cpk is the smaller of Cpu or Cpl (same for the P versions) when a process has both an upper and lower specification limit.

• Cpl or Ppl = Indicates capability when only a lower specification limit exists (Ex: amt. of chicken in frozen pot pie cannot be less than 1 oz)
• Cpu or Ppu = Indicates capability when only an upper specification limit exists (Ex: delivery time cannot exceed 24 hours)
• Calculate both values and report the smaller number
• Typical goals for capability indices are greater than 1.33 (or 1.67 if safety related)
• Give highest priority to parameters with capability indices of less than 1.0 (you want to center the process around the specification, reduce the variation, or both)
  • If product/process is mature, and there have been no customer problems, see if defined tolerances can be changed—what is the need for a formal spec if another "de facto" spec has been used historically?
  • May need to perform 100% inspection, measuring, and sorting until the process is improved

Tips 

• Check short-term capability first. If unacceptable, implement fixes. If acceptable, then run a long-term capability analysis. (Repeat customers, after all, experience the long-term capability of the process.)
  • Research the sources of variability and identify as best you can how often each is likely to appear
  • Calculate the process capability performance once you have determined that it's likely at least 80% of the variability has been seen
• Check what really happens in the workplace to see if there are unwritten specifications that people use in addition to or instead of the documented specifications. Evaluating results against written specifications when people are using unwritten specifications can lead to false conclusions.