DFT LINEARITY
The DFT has a very important property known as linearity. This property states that the DFT of the sum of two signals is equal to the sum of the transforms of each signal; that is, if an input sequence x1(n) has a DFT X1(m) and another input sequence x2(n) has a DFT X2(m), then the DFT of the sum of these sequences xsum(n) = x1(n) + x2(n) is
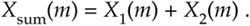
This is certainly easy enough to prove. If we plug xsum(n) into Eq. (3-2) to get Xsum(m), then
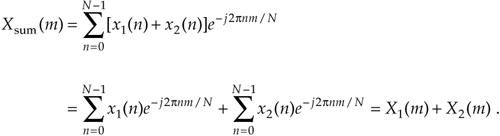
Without this property of linearity, the DFT would be useless as an analytical tool because we could transform only those input signals that contain a single sinewave. The real-world signals that we want to analyze are much more complicated than a single sinewave.
URL http://proquest.safaribooksonline.com/0131089897/ch03lev1sec3
 |
Amazon |  |
