Section E.2. SOME USEFUL DECIBEL NUMBERS | Appendix E. Decibels (dB and dBm)

Table of contents:

E 2 SOME USEFUL DECIBEL NUMBERS

E 2 SOME USEFUL DECIBEL NUMBERS

If the reader uses dB scales on a regular basis, there are a few constants worth committing to memory. A power difference of 3 dB corresponds to a power factor of 2; that is, if the magnitude-squared ratio of two different frequency components is 2, then from Eq. (E-2),

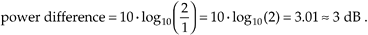
Likewise, if the magnitude-squared ratio of two different frequency components is 1/2, then the relative power difference is –3 dB because

Table E-1. Some seful Logarithmic Relationships

Magnitude ratio	Magnitude-squared power (P1/P2) ratio	Relative dB (approximate)
10–1/2	10–1	–10	P1 is one-tenth P2
2–1	2–2 = 1/4	–6	P1 is one-fourth P2
2–1/2	2–1 = 1/2	–3	P1 is one-half P2
20	20 = 1	0	P1 is equal to P2
21/2	21 = 2	3	P1 is twice P2
21	22 = 4	6	P1 is four times P2
101/2	101 = 10	10	P1 is ten times P2
101	102 = 100	20	P1 is one hundred times P2
103/2	103 = 1000	30	P1 is one thousand times P2

Equation E-9

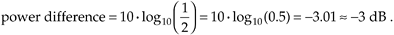
Table E-1 lists several magnitude and power ratios vs. dB values worth remembering. Keep in mind that decibels indicate only relative power relationships. For example, if we're told that signal A is 6 dB above signal B, we know that the power of signal A is four times that of signal B, and that the magnitude of signal A is twice the magnitude of signal B. We may not know the absolute power of signals A and B in watts, but we do know that the power ratio is PA/PB = 4.

URL http://proquest.safaribooksonline.com/0131089897/app05lev1sec2