DFT FREQUENCY AXIS
The frequency axis m of the DFT result in Figure 3-4 deserves our attention once again. Suppose we hadn't previously seen our DFT Example 1, were given the eight input sample values, from Eq. (3-11'), and asked to perform an 8-point DFT on them. We'd grind through Eq. (3-2) and get the X(m) values shown in Figure 3-4. Next we ask, "What's the frequency of the highest magnitude component in X(m) in Hz?" The answer is not "1." The answer depends on the original sample rate fs. Without prior knowledge, we have no idea over what time interval the samples were taken, so we don't know the absolute scale of the X(m) frequency axis. The correct answer to the question is to take fs and plug it into Eq. (3-5) with m = 1. Thus, if fs = 8000 samples/s, then the frequency associated with the largest DFT magnitude term is
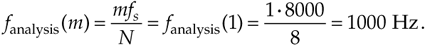
If we said the sample rate fs was 75 samples/s, we'd know, from Eq. (3-5), that the frequency associated with the largest magnitude term is now
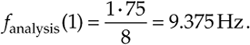
OK, enough of this—just remember that the DFT's frequency spacing (resolution) is fs/N.
To recap what we've learned so far:
- each DFT output term is the sum of the term-by-term products of an input time-domain sequence with sequences representing a sine and a cosine wave,
- for real inputs, an N-point DFT's output provides only N/2+1 independent terms,
- the DFT is a linear operation,
- the magnitude of the DFT results are directly proportional to N, and
- the DFT's frequency resolution is fs/N.
It's also important to realize, from Eq. (3-5), that X(N/2+1), when m = N/2+1, corresponds to half the sample rate, i.e., the folding (Nyquist) frequency fs/2.
 |
Amazon |  |
