INTERPOLATING A BANDPASS SIGNAL
There are many digital communications applications where a real signal is centered at one fourth the sample rate, or fs/4. This condition makes quadrature downconversion particularly simple. (See Sections 8.9 and 13.1.) In the event that you'd like to generate an interpolated (increased sample rate) version of the bandpass signal but maintain its fs/4 center frequency, there's an efficient way to do so[37]. Suppose we want to interpolate by a factor of two so the output sample rate is twice the input sample rate, fs-out = 2fs-in. In this case the process is: quadrature downconversion by fs-in/4, interpolation factor of two, quadrature upconversion by fs-out/4, and then take only the real part of the complex upconverted sequence. The implementation of this scheme is shown at the top of Figure 13-36.
Figure 13-36. Bandpass signal interpolation scheme, and spectra.
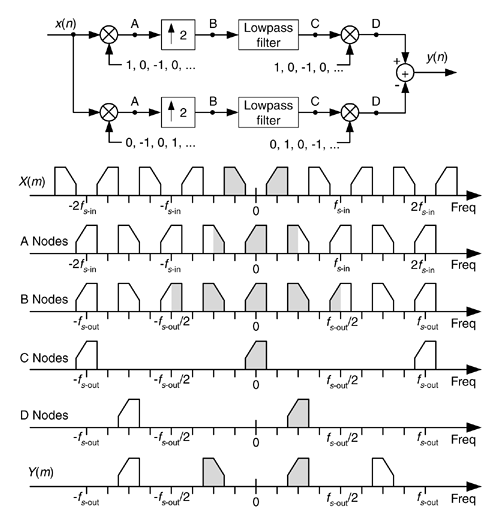
The sequences applied to the first multiplier in the top signal path are the real x(n) input and the repeating mixing sequence 1,0,–1,0. That mixing sequence is the real (or in-phase) part of the complex exponential
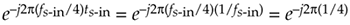
needed for quadrature downconversion by fs/4. Likewise, the repeating mixing sequence 0,–1,0,1 applied to the first multiplier in the bottom path is the imaginary (or quadrature phase) part of the complex downconversion exponential 
. The 
2 symbol means insert one zero-valued sample between each signal at the A nodes. The final subtraction to obtain y(n) is how we extract the real part of the complex sequence at Node D. (That is, we're extracting the real part of the product of the complex signal at Node C times ej2p(1/4).) The spectra at various nodes of this process are shown at the bottom of Figure 13-35. The shaded spectra indicate true spectral components, while the white spectra represent spectral replications. Of course, the same lowpass filter must be used in both processing paths to maintain the proper time delay and orthogonal phase relationships.
There are several additional issues worth considering regarding this interpolation process[38]. If the amplitude loss, inherent in interpolation, of a factor of two is bothersome, we can make the final mixing sequences 2,0,–2,0, and 0,2,0,–2 to compensate for that loss. Because there are so many zeros in the sequences at Node B (three/fourths of the samples), we should consider those efficient polyphase filters for the lowpass filtering. Finally, if it's sensible in your implementation, consider replacing the final adder with a multiplexer (because alternate samples of the sequences at Node D are zeros). In this case, the mixing sequence in the bottom path would be changed to 0,–1,0,1.
URL http://proquest.safaribooksonline.com/0131089897/ch13lev1sec14
 |
Amazon |  |
