COMPLEX DOWN-CONVERSION
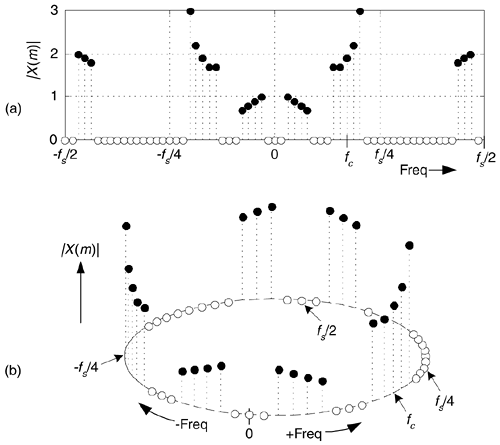
Complex down-conversion of discrete signal is a straightforward process, and best described by an example. Think of a real-valued discrete sequence x(n) having an |X(m)| spectral magnitude whose non-zero-valued samples are shown as the solid dots in Figure 8-14(a). Because of the periodicity of discrete spectral representations we discussed in Sections 2.1 and 3.17 (as well as the frequency axis of the FFT lying on the unit circle in the z-plane explained in Section 6.3), we're justified in also representing the |X(m)| spectrum as the three-dimensional circular plot given in Figure 8-14(b). There we've wrapped the linear frequency axis of Figure 8-14(a) around a circle whose perimeter length is equal to the sample rate fs such that the frequencies fs/2 and –fs/2 are the same point on the circular axis.
Figure 8-14. Discrete X(m) spectra of a real-valued time sequence: (a) traditional depiction; (b) circular frequency axis depiction.
With x(n) being an N-point real sequence, |X(m)|'s spectrum is symmetrical about the zero-frequency point. If we now perform complex down-conversion (by multiplying x(n) by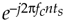 
, where ts = 1/fs, using either equivalent scheme shown in Figure 8-15(a)), the result is the complex sequence xc(n) = i(n) + jq(n) whose spectrum is given in Figure 8-15(b). The minus sign in the exponent of 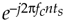shifts the |X(m)| spectrum fc Hz in the negative-frequency direction. Of course, because xc(n) is complex, there's no symmetry about the zero-frequency point in |Xc(m)|. The circular depiction of |Xc(m)| is provided in Figure 8-15(c). The i(n) and q(n) parts of sequence xc(n) are said to be orthogonal, meaning they are independent of, and do not affect, each other and the following condition holds:
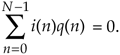
Figure 8-15. Discrete |Xc(m)| spectra of a down-converted time sequence: (a) down-conversion symbols; (b) traditional frequency axis depiction; (c) circular frequency axis depiction.
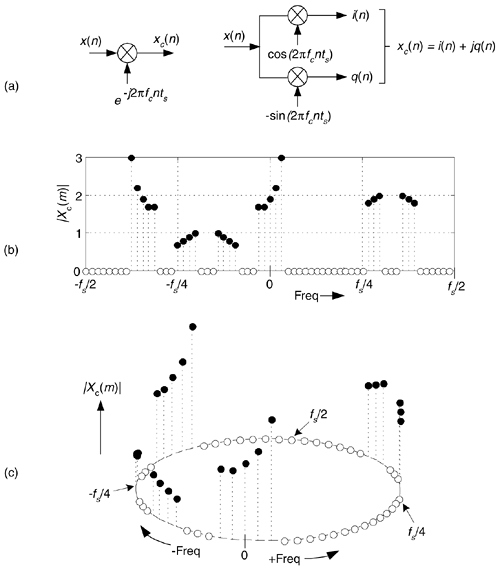
The purpose of the Figures 8-14 and 8-15 is to show how frequency translation by means of complex down-conversion causes spectral components to wrap around the fs/2 point.
Figure 8-15(a) showed the method of down-converting a real x(n) time sequence. For completeness, Figure 8-16 shows how translating a complex time sequence xc(n) = i(n) + jq(n) up or down by fc Hz requires a complex multiplier.
Figure 8-16. Complex multiplier used for up/down-conversion.
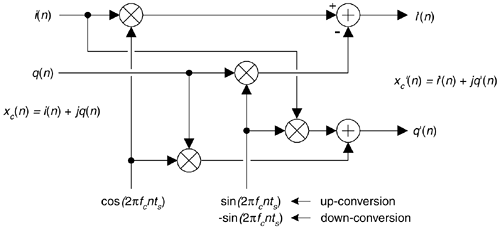
This complex multiplier computes
Equation 8-18
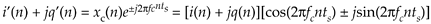
If you use this multiplier, don't forget the minus sign at the top adder in Figure 8-16. (It's an easy mistake to make. Believe me.)
URL http://proquest.safaribooksonline.com/0131089897/ch08lev1sec7
 |
Amazon |  |
