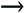FLOATING-POINT BINARY FORMATS | Chapter Twelve. Digital Data Formats and Their Effects

Floating-point binary formats allow us to overcome most of the limitations of precision and dynamic range mandated by fixed-point binary formats, particularly in reducing the ill effects of overflow [19]. Floating-point formats segment a data word into two parts: a mantissa m and an exponent e. Using these parts, the value of a binary floating-point number n is evaluated as that is, the number's value is the product of the mantissa and 2 raised to the power of the exponent. (Mantissa is a somewhat unfortunate choice of terms because it has a meaning here very different from that in the mathematics of logarithms. Mantissa originally meant the decimal fraction of a logarithm.[] However, due to its abundance in the literature we'll continue using the term mantissa here.) Of course, both the mantissa and the exponent in Eq. (12-27) can be either positive or negative numbers.

[] For example, the common logarithm (log to the base 10) of 256 is 2.4082. The 2 to the left of the decimal point is called the characteristic of the logarithm and the 4082 digits are called the mantissa. The 2 in 2.4082 does not mean that we multiply .4082 by 102. The 2 means that we take the antilog of .4082 to get 2.56 and multiply that by 102 to get 256.

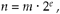
Let's assume that a b-bit floating-point number will use be bits for the fixed-point signed exponent and bm bits for the fixed-point signed mantissa. The greater the number of be bits used, the larger the dynamic range of the number. The more bits used for bm, the better the resolution, or precision, of the number. Early computer simulations conducted by the developers of b-bit floating-point formats indicated that the best trade-off occurred with be 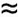b/4 and bm 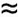3b/4. 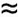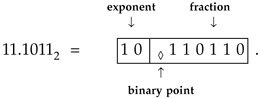We'll see that, for typical 32-bit floating-point formats used today, be 8 bits and bm 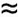24 bits. To take advantage of a mantissa's full dynamic range, most implementations of floating-point numbers treat the mantissa as a fractional fixed-point binary number, shift the mantissa bits to the right or left, so that its most significant bit is a one, and adjust the exponent accordingly. This convention is called normalization. When normalized, the mantissa bits are typically called the fraction of the floating-point number, instead of the mantissa. For example, the decimal value 3.687510 can be represented by the fractional binary number 11.10112. If we use a two-bit exponent with a six-bit fraction floating-point word, we can just as well represent 11.10112 by shifting it to the right two places and setting the exponent to two as

Equation 12-28

The floating-point word above can be evaluated to retrieve our decimal number again as

Equation 12-29

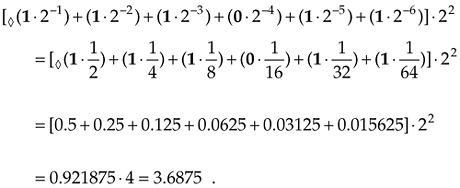
After some experience using floating-point normalization, users soon realized that always having a one in the most significant bit of the fraction was wasteful. That redundant one was taking up a single bit position in all data words and serving no purpose. So practical implementations of floating-point formats discard that one, assume its existence, and increase the useful number of fraction bits by one. This is why the term hidden bit is used to describe some floating-point formats. While increasing the fraction's precision, this scheme uses less memory because the hidden bit is merely accounted for in the hardware arithmetic logic. Using a hidden bit, the fraction in Eq. (12-28)'s floating point number is shifted to the left one place and would now be

Equation 12-30

Recall that the exponent and mantissa bits were fixed-point signed binary numbers, and we've discussed several formats for representing signed binary numbers, i.e., sign magnitude, two's complement, and offset binary. As it turns out, all three signed binary formats are used in industry-standard floating-point formats. The most common floating-point formats, all using 32-bit words, are listed in Table 12-3.

The IEEE P754 floating-point format is the most popular because so many manufacturers of floating-point integrated circuits comply with this standard [8, 20–22]. Its exponent e is offset binary (biased exponent), and its fraction is a sign-magnitude binary number with a hidden bit that's assumed to be 20. The decimal value of a normalized IEEE P754 floating-point number is evaluated as

Equation 12-31

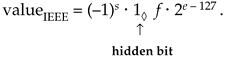
The IBM floating-point format differs somewhat from the other floating-point formats because it uses a base of 16 rather than 2. Its exponent is offset binary, and its fraction is sign magnitude with no hidden bit. The decimal value of a normalized IBM floating-point number is evaluated as

Equation 12-32

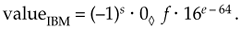
Table 12-3. Floating–Point Number Formats

IEEE Standard P754 Format
Bit	31	30	29	28	27	26	25	24	23	22	21	20	. . .	2	1	0
	S	27	26	25	24	23	22	21	20	2–1	2–2	2–3	. . .	2–21	2–22	2–23
Sign (s)		Exponent (e)								Fraction (f)
IBM Format
Bit	31	30	29	28	27	26	25	24	23	22	21	20	. . .	2	1	0
	S	26	25	24	23	22	21	20	2–1	2–2	2–3	2–4	. . .	2–22	2–23	2–24
Sign (s)		Exponent (e)							Fraction (f)
DEC (Digital Equipment Corp.) Format
Bit	31	30	29	28	27	26	25	24	23	22	21	20	. . .	2	1	0
	S	27	26	25	24	23	22	21	20	2–2	2–3	2–4	. . .	2–22	2–23	2–24
Sign (s)		Exponent (e)								Fraction (f)
MIL–STD 1750A Format
Bit	31	30	29	. . .	11	10	9	8	7	6	5	4	3	2	1	0
	20	2–1	2–2	. . .	2–20	2–21	2–22	2–23	27	26	25	24	23	22	21	20
Fraction (f)									Exponent (e)

The DEC floating-point format uses an offset binary exponent, and its fraction is sign magnitude with a hidden bit that's assumed to be 2–1. The decimal value of a normalized DEC floating-point number is evaluated as

Equation 12-33

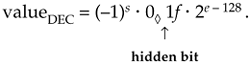
MIL-STD 1750A is a United States Military Airborne floating-point standard. Its exponent e is a two's complement binary number residing in the least significant eight bits. MIL-STD 1750A's fraction is also a two's complement number (with no hidden bit), and that's why no sign bit is specifically indicated in Table 12-3. The decimal value of a MIL-STD 1750A floating-point number is evaluated as

Equation 12-34

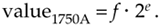
Notice how the floating-point formats in Table 12-3 all have word lengths of 32 bits. This was not accidental. Using 32-bit words makes these formats easier to handle using 8-, 16-, and 32-bit hardware processors. That fact not withstanding and given the advantages afforded by floating-point number formats, these formats do require a significant amount of logical comparisons and branching to correctly perform arithmetic operations. Reference [23] provides useful flow charts showing what procedural steps must be taken when floating-point numbers are added and multiplied.

12.4.1 Floating-Point Dynamic Range

Attempting to determine the dynamic range of an arbitrary floating-point number format is a challenging exercise. We start by repeating the expression for a number system's dynamic range from Eq. (12-6) as

Equation 12-35

When we attempt to determine the largest and smallest possible values for a floating-point number format, we quickly see that they depend on such factors as

the position of the binary point
whether a hidden bit is used or not (If used, its position relative to the binary point is important.)
the base value of the floating-point number format
the signed binary format used for the exponent and the fraction (For example, recall from Table 12-2 that the binary two's complement format can represent larger negative numbers than the sign-magnitude format.)
how unnormalized fractions are handled, if at all. (Unnormalized, also called gradual underflow, means a nonzero number that's less than the minimum normalized format but can still be represented when the exponent and hidden bit are both zero.)
how exponents are handled when they're either all ones or all zeros. (For example, the IEEE P754 format treats a number having an all ones exponent and a nonzero fraction as an invalid number, whereas the DEC format handles a number having a sign = 1 and a zero exponent as a special instruction instead of a valid number.)

Trying to develop a dynamic range expression that accounts for all the possible combinations of the above factors is impractical. What we can do is derive a rule of thumb expression for dynamic range that's often used in practice[8,22,24].

Let's assume the following for our derivation: the exponent is a be-bit offset binary number, the fraction is a normalized sign-magnitude number having a sign bit and bm magnitude bits, and a hidden bit is used just left of the binary point. Our hypothetical floating-point word takes the following form:

Bit		bm+be–1	bm+be–2	· · ·	bm+2	bm	bm–1	bm–2	. . .	1	0
	S	2be–1	2be–2	· · ·	21	20	2–1	2–2	. . .	2–bm+1	2–bm
Sign (s)		Exponent (e)					Fraction (f)

First we'll determine what the largest value can be for our floating-point word. The largest fraction is a one in the hidden bit, and the remaining bm fraction bits are all ones. This would make fraction 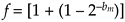The first 1 in this expression is the hidden bit to the left of the binary point, and the value in parentheses is all bm bits equal to ones to the right of the binary point. The greatest positive value we can have for the be-bit offset binary exponent is . So the largest value that can be represented with the floating-point number is the largest fraction raised to the largest positive exponent, or

Equation 12-36

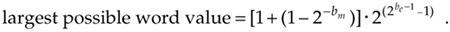
The smallest value we can represent with our floating-point word is a one in the hidden bit times two raised to the exponent's most negative value, , or

Equation 12-37

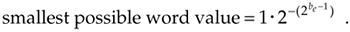
Plugging Eqs. (12-36) and (12-37) into Eq. (12-35),

Equation 12-38

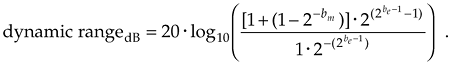
Now here's where the thumb comes in—when bm is large, say over seven, the 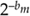value approaches zero; that is, as bm increases, the all ones fraction 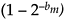value in the numerator approaches 1. Assuming this, Eq. (12-38) becomes

Equation 12-39

Using Eq. (12-39) we can estimate, for example, the dynamic range of the single-precision IEEE P754 standard floating-point format with its eight-bit exponent:

Equation 12-40

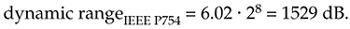
Although we've introduced the major features of the most common floating-point formats, there are still more details to learn about floating-point numbers. For the interested reader, the references given in this section provide a good place to start.

URL http://proquest.safaribooksonline.com/0131089897/ch12lev1sec4