A FEW THOUGHTS ON NEGATIVE FREQUENCY
It's important for us to be comfortable with the concept of negative frequency because it's essential in understanding the spectral replication effects of periodic sampling, discrete Fourier transforms, and the various quadrature signal processing techniques discussed in Chapter 9. The convention of negative frequency serves as both a consistent and powerful mathematical tool in our analysis of signals. In fact, the use of negative frequency is mandatory when we represent real signals, such as a sine or cosine wave, in complex notation.
The difficulty in grasping the idea of negative frequency may be, for some, similar to the consternation felt in the parlors of mathematicians in the Middle Ages when they first encountered negative numbers. Until the thirteenth century, negative numbers were considered fictitious because numbers were normally used for counting and measuring. So up to that time, negative numbers just didn't make sense. In those days, it was valid to ask, "How can you hold in your hand something that is less than nothing?" The idea of subtracting six from four must have seemed meaningless. Math historians suggest that negative numbers were first analyzed in Italy. As the story goes, around the year 1200 the Italian mathematician Leonardo da Pisa (known as Fibonacci) was working on a financial problem whose only valid solution involved a negative number. Undaunted, Leo wrote, "This problem, I have shown to be insoluble unless it is conceded that the first man had a debt."
Thus negative numbers arrived on the mathematics scene, never again to be disregarded.
Modern men and women can now appreciate that negative numbers have a direction associated with them. The direction is backward from zero in the context that positive numbers point forward from zero. For example, negative numbers can represent temperatures measured in degrees below zero, minutes before the present if the present is considered as zero time, or money we owe the tax collector when our income is considered positive dollars. So, the notion of negative quantities is perfectly valid if we just define it properly. As comfortable as we now are with negative numbers, negative frequency remains a troublesome and controversial concept for many engineers[3,4]. This author once encountered a paper in a technical journal which stated: "since negative frequencies cannot exist—." Well, like negative numbers, negative frequency is a perfectly valid concept as long as we define it properly relative to what we're used to thinking of as positive frequency. With this thought in mind, we'll call Figure 8-5's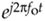 
signal a positive-frequency complex exponential because it rotates around the complex plane's origin in a circle in a positive-angle direction at a cyclic frequency of fo cycles per second. Likewise, we'll refer to the 
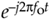signal as a negative-frequency complex exponential because of its negative-angle direction of rotation.
So we've defined negative frequency in the frequency domain. If my DSP pals want to claim negative frequency doesn't exist in the time domain, I won't argue. However, our frequency-domain negative frequency definition is clean, consistent with real signals, very useful, and here to stay.
 |
Amazon |  |
