DFT SCALLOPING LOSS | Chapter Three. The Discrete Fourier Transform

Scalloping is the name used to describe fluctuations in the overall magnitude response of an N-point DFT. Although we derive this fact in Section 3.16, for now we'll just say that when no input windowing function is used, the sin(x)/x shape of the sinc function's magnitude response applies to each DFT output bin. Figure 3-19(a) shows a DFT's aggregate magnitude response by superimposing several sin(x)/x bin magnitude responses.[] (Because the sinc function's sidelobes are not key to this discussion, we don't show them in Figure 3-19(a).) Notice from Figure 3-19(b) that the overall DFT frequency-domain response is indicated by the bold envelope curve. This rippled curve, also called the picket fence effect, illustrates the processing loss for input frequencies between the bin centers.

[] Perhaps Figure 3-19(a) is why individual DFT outputs are called "bins." Any signal energy under a sin(x)/x curve will show up in the enclosed storage compartment of that DFT's output sample.

Figure 3-19. DFT bin magnitude response curves: (a) individual sin(x)/x responses for each DFT bin; (b) equivalent overall DFT magnitude response.

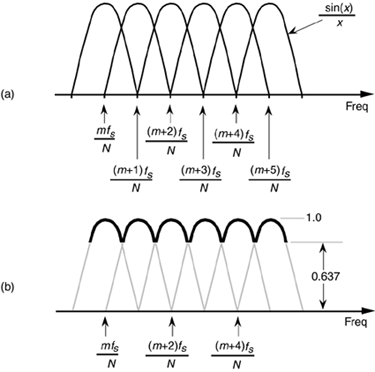
From Figure 3-19(b), we can determine that the magnitude of the DFT response fluctuates from 1.0, at bin center, to 0.637 halfway between bin centers. If we're interested in DFT output power levels, this envelope ripple exhibits a scalloping loss of almost –4 dB halfway between bin centers. Figure 3-19 illustrates a DFT output when no window (i.e., a rectangular window) is used. Because nonrectangular window functions broaden the DFT's main lobe, their use results in a scalloping loss that will not be as severe as the rectangular window[10,12]. That is, their wider main lobes overlap more and fill in the valleys of the envelope curve in Figure 3-19(b). For example, the scalloping loss of a Hanning window is approximately 0.82, or –1.45 dB, halfway between bin centers. Scalloping loss is not, however, a severe problem in practice. Real-world signals normally have bandwidths that span many frequency bins so that DFT magnitude response ripples can go almost unnoticed. Let's look at a scheme called zero padding that's used to both alleviate scalloping loss effects and to improve the DFT's frequency resolution.