APPROXIMATE ENVELOPE DETECTION
In this section, we present a crude (but simple to implement) complex signal envelope detection scheme. By envelope detection, we mean estimating the instantaneous magnitude of a complex signal xc(n). The process is straightforward: we sum the absolute values of a complex signal's real and imaginary parts, and apply that sum to a simple first-order lowpass IIR filter to obtain an envelope signal E(n) as shown in Figure 13-78(a). The filter's feedback coefficient a is in the range of 0 to 1. (That lowpass filter is our exponential averager discussed in Section 11.5, which some DSP folks call a leaky integrator.) The E(n) sequence is proportional to the desired instantaneous magnitude of xc(n), or
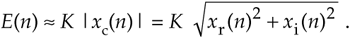
Figure 13-78. Envelope detection: (a) block diagram; (b) |xr(n)|+|xi(n)| adder output, and E(n) for a = 0.4; (c) E(n) for a = 0.7 and a = 0.9.
To gauge the envelope detector's performance, consider a sampled version of an amplitude modulated sinusoid such as the xr(n) in Figure 9-7(a) from which a sampled analytic (complex) xc(n) can been generated. If xc(n) is applied to our envelope detection process, the processing results are shown in Figure 13-78(b) and 13-78(c), where the solid curves represent E(n) and the dashed curves are the true magnitude of xc(n). Notice how the amount of smoothing of the E(n) fluctuations depends on the value of a.
Sequence xr(n) must be used to generate a complex analytic xc(n) sequence (using one of the methods discussed in Sections 9.4 and 9.5) upon which this envelope detector scheme can be applied. The advantage of this envelope detection process is that, of course, no squaring or square root computations in Eq. (13-133), nor the |xr(n)| and |xi(n)| comparisons in the vector magnitude approximations in Section 13.2, need be performed.
Whether this envelope approximation technique yields sufficiently accurate results is for the user to decide. Its accuracy may be below the requirements of most AM (amplitude modulation) detection requirements, but the process may well be useful for estimating signal magnitude in automatic gain control (AGC) or energy detection applications.
URL http://proquest.safaribooksonline.com/0131089897/ch13lev1sec31
 |
Amazon |  |
