REDUCING A/D CONVERTER QUANTIZATION NOISE
REDUCING A D CONVERTER QUANTIZATION NOISE
In Section 12.3 we discussed the mathematical details, and ill effects, of quantization noise in analog-to-digital (A/D) converters. DSP practitioners commonly use two tricks to reduce converter quantization noise. Those schemes are called oversampling and dithering.
13.8.1 Oversampling
The process of oversampling to reduce A/D converter quantization noise is straightforward. We merely sample an analog signal at an fs sample rate higher than the minimum rate needed to satisfy the Nyquist criterion (twice the analog signal's bandwidth), and then lowpass filter. What could be simpler? The theory behind oversampling is based on the assumption that an A/D converter's total quantization noise power (variance) is the converter's least significant bit (lsb) value squared over 12, or
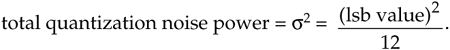
We derived that expression in Section 12.3. The next assumption is: the quantization noise values are truly random, and in the frequency domain the quantization noise has a flat spectrum. (These assumptions are valid if the A/D converter is being driven by an analog signal that covers most of the converter's analog input voltage range, and is not highly periodic.) Next we consider the notion of quantization noise power spectral density (PSD), a frequency-domain characterization of quantization noise measured in noise power per hertz as shown in Figure 13-17. Thus we can consider the idea that quantization noise can be represented as a certain amount of power (watts, if we wish) per unit bandwidth.
Figure 13-17. Frequency-domain power spectral density of an ideal A/D converter.

In our world of discrete systems, the flat noise spectrum assumption results in the total quantization noise (a fixed value based on the converter's lsb voltage) being distributed equally in the frequency domain, from –fs/2 to +fs/2 as indicated in Figure 13-17. The amplitude of this quantization noise PSD is the rectangle area (total quantization noise power) divided by the rectangle width (fs), or
Equation 13-65
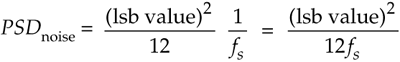
measured in watts/Hz.
The next question is: "How can we reduce the PSDnoise level defined by Eq. (13-65)?" We could reduce the lsb value (volts) in the numerator by using an A/D converter with additional bits. That would make the lsb value smaller and certainly reduce PSDnoise, but that's an expensive solution. Extra converter bits cost money. Better yet, let's increase the denominator of Eq. (13-65) by increasing the sample rate fs.
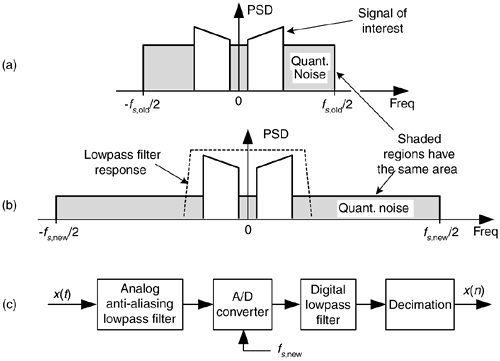
Consider a low-level discrete signal of interest whose spectrum is depicted in Figure 13-18(a). By increasing the fs,old sample rate to some larger value fs,new (oversampling), we spread the total noise power density (a fixed value) over a wider frequency range as shown in Figure 13-18(b). The area under the shaded curves in Figure 13-18(a) and 13-18(b) are equal. Next we lowpass filter the converter's output samples. At the output of the filter, the quantization noise level contaminating our signal will be reduced from that at the input of the filter.
Figure 13-18. Oversampling example: (a) noise PSD at an fs,old samples rate; (b) noise PSD at the higher fs,new samples rate; (c) processing steps.
The improvement in signal to quantization noise ratio, measured in dB, achieved by oversampling is:
Equation 13-66
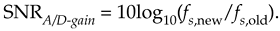
For example: if fs,old = 100 kHz, and fs,new = 400 kHz, the SNRA/D-gain = 10log10(4) = 6.02 dB. Thus oversampling by a factor of 4 (and filtering), we gain a single bit's worth of quantization noise reduction. Consequently we can achieve N+1-bit performance from an N-bit A/D converter, because we gain signal amplitude resolution at the expense of higher sampling speed. After digital filtering, we can decimate to the lower fs,old without degrading the improved SNR. Of course, the number of bits used for the lowpass filter's coefficients and registers must exceed the original number of A/D converter bits, or this oversampling scheme doesn't work.
With the use of a digital lowpass filter, depending on the interfering analog noise in x(t), it's possible to use a lower performance (simpler) analog anti-aliasing filter relative to the analog filter necessary at the lower sampling rate.
13.8.2 Dithering
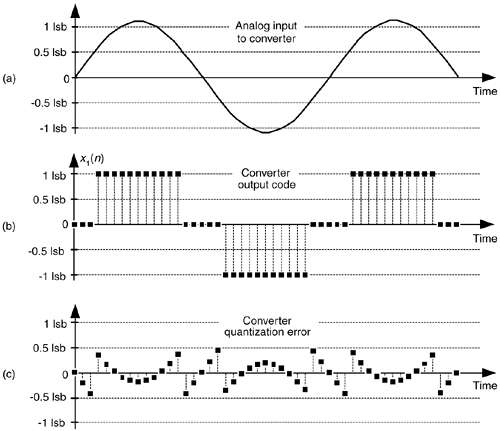
Dithering, another technique used to minimize the effects of A/D quantization noise, is the process of adding noise to our analog signal prior to A/D conversion. This scheme, which doesn't seem at all like a good idea, can indeed be useful and is easily illustrated with an example. Consider digitizing the low-level analog sinusoid shown in Figure 13-19(a), whose peak voltage just exceeds a single A/D converter least significant bit (lsb) voltage level, yielding the converter output x1(n) samples in Figure 13-19(b). The x1(n) output sequence is clipped. This generates all sorts of spectral harmonics. Another way to explain the spectral harmonics is to recognize the periodicity of the quantization noise in Figure 13-19(c).
Figure 13-19. Dithering: (a) a low-level analog signal; (b) the A/D converter output sequence; (c) the quantization error in the converter's output.
We show the spectrum of x1(n) in Figure 13-20(a) where the spurious quantization noise harmonics are apparent. It's worthwhile to note that averaging multiple spectra will not enable us to pull some spectral component of interest up above those spurious harmonics in Figure 13-20(a). Because the quantization noise is highly correlated with our input sinewave—the quantization noise has the same time period as the input sinewave—spectral averaging will also raise the noise harmonic levels. Dithering to the rescue.
Figure 13-20. Spectra of a low-level discrete sinusoid: (a) with no dithering; (b) with dithering.
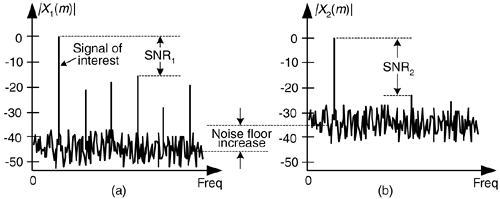
Dithering is the technique where random analog noise is added to the analog input sinusoid before it is digitized. This technique results in a noisy analog signal that crosses additional converter lsb boundaries and yields a quantization noise that's much more random, with a reduced level of undesirable spectral harmonics as shown in Figure 13-20(b). Dithering raises the average spectral noise floor but increases our signal to noise ratio SNR2. Dithering forces the quantization noise to lose its coherence with the original input signal, and we could then perform signal averaging if desired.
Dithering is indeed useful when we're digitizing
- low-amplitude analog signals,
- highly periodic analog signals (like a sinewave with an even number of cycles in the sample time interval), and
- slowly varying (very low frequency, including DC) analog signals.
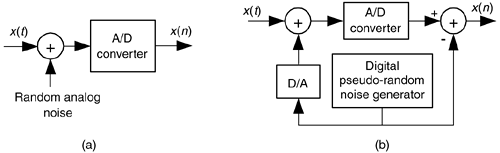
The standard implementation of dithering is shown in Figure 13-21(a). The typical amount of random wideband analog noise used in the this process, provided by a noise diode or noise generator ICs, has a rms level equivalent to 1/3 to 1 lsb voltage level.
Figure 13-21. Dithering implementations: (a) standard dithering process; (b) advanced dithering with noise subtraction.
For high-performance audio applications, engineers have found that adding dither noise from two separate noise generators improves background audio low-level noise suppression. The probability density function (PDF) of the sum of two noise sources (having rectangular PDFs) is the convolution of their individual PDFs. Because the convolution of two rectangular functions is triangular, this dual-noise-source dithering scheme is called triangular dither. Typical triangular dither noise has rms levels equivalent to, roughly, 2 lsb voltage levels.
In the situation where our signal of interest occupies some well defined portion of the full frequency band, injecting narrowband dither noise having an rms level equivalent to 4 to 6 lsb voltage levels, whose spectral energy is outside that signal band, would be advantageous. (Remember though: the dither signal can't be too narrowband, like a sinewave. Quantization noise from a sinewave signal would generate more spurious harmonics!) That narrowband dither noise can then be removed by follow-on digital filtering.
One last note about dithering: to improve our ability to detect low-level signals, we could add the analog dither noise and then subtract that noise from the digitized data, as shown in Figure 13-21(b). This way, we randomized the quantization noise, but reduced the amount of total noise power injected in the analog signal. This scheme is used in commercial analog test equipment[22,23].
URL http://proquest.safaribooksonline.com/0131089897/ch13lev1sec8
 |
Amazon |  |
