HIGHPASS FIR FILTER DESIGN
Going one step further, we can use the bandpass FIR filter design technique to design a highpass FIR filter. To obtain the coefficients for a highpass filter, we need only modify the shifting sequence sshift(k) to make it represent a sampled sinusoid whose frequency is fs/2. This process is shown in Figure 5-29. Our final 31-tap highpass FIR filter's hhp(k) coefficients are
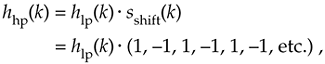
Figure 5-29. Highpass filter with frequency response centered at fs/2: (a) generating 31-tap filter coefficients hhp(k); (b) frequency magnitude response |Hhp(m)|.
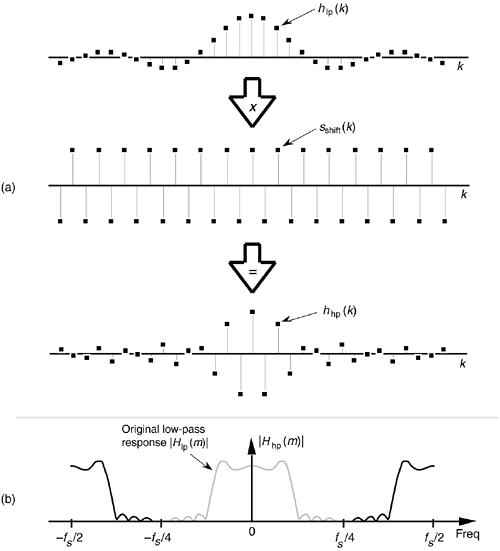
whose |Hhp(m)| frequency response is the solid curve in Figure 5-29(b). Because sshift(k) in Figure 5-29(a) has alternating plus and minus ones, we can see that hhp(k) is merely hlp(k) with the sign changed for every other coefficient. Unlike |Hbp(m)| in Figure 5-28(b), the |Hhp(m)| response in Figure 5-29(b) has the same amplitude as the original |Hlp(m)|.
Again, notice that the hlp(k) low-pass coefficients in Figure 5-29(a) have not been modified by any window function. In practice, we'd use a windowed hlp(k) to reduce the passband ripple before implementing Eq. (5-21).
URL http://proquest.safaribooksonline.com/0131089897/ch05lev1sec5
 |
Amazon |  |
