INCOHERENT AVERAGING | Chapter Eleven. Signal Averaging

The process of incoherent averaging (also known as rms, postdetection, scalar, or video averaging) is the averaging of signal samples where no sample timing constraints are used; that is, signal measurement time intervals are not synchronized in any way with the phase of the signal being measured. Think for a moment what the average would be of the noisy pulse signal in Figure 11-1(a) if we didn't in some way synchronize the beginning of the collection of the individual signal sample sets with the beginning of the pulse. The result would be pulses that begin at a different time index in each sample set. The averaging of multiple sample sets would then smear the pulse across the sample set, or just "average the pulse signal away." (For those readers familiar with using oscilloscopes, incoherent averaging would be like trying to view the pulse when the beginning of the scope sweep was not triggered by the signal.) As such, incoherent averaging is not so useful in the time domain.[] In the frequency domain, however, it's a different story because incoherent averaging can provide increased accuracy in measuring relative signal powers. Indeed, incoherent averaging is used in many test instruments, such as spectrum, network, and signal analyzers.

[] The term incoherent averaging is a bit of a misnomer. Averaging a set of data is just that, averaging—we add up a set of data values and divide by the number of samples in the set. Incoherent averaging should probably be called averaging data that's obtained incoherently.

In some analog test equipment, time-domain signals are represented in the frequency domain using a narrowband sweeping filter followed by a power detector. These devices measure signal power as a function of frequency. The power detector is necessary because the sweeping measurement is not synchronized, in time, with the signal being measured. Thus the frequency-domain data represents power only and contains no signal phase information. Although it's too late to improve the input's signal-amplitude-to-noise ratio, incoherent averaging can improve the accuracy of signal power measurements in the presence of noise; that is, if the signal-power spectrum is very noisy, we can reduce the power estimation fluctuations and improve the accuracy of signal-power and noise-power measurements. Figure 11-4(a) illustrates this idea where we see the power (magnitude squared) output of an FFT of a fundamental tone and several tone harmonics buried in background noise. Notice that the noise-power levels in Figure 11-4(a) fluctuate by almost 20 dB about the true average noise power indicated by the dashed line at –19 dB.

Figure 11-4. Results of averaging signal tones plus noise-power spectra: (a) no averaging, N = 1; (b) N = 10; (c) N = 100.

If we take 10 FFTs, average the square of their output magnitudes, and normalize those squared values, we get the power spectrum shown in Figure 11-4(b). Here, we've reduced the variance of the noise in the power spectrum but have not improved the tones' signal-power-to-noise-power ratios; that is, the average noise-power level remains unchanged. Averaging the output magnitudes squared of 100 FFTs results in the spectrum in Figure 11-4(c), which provides a more accurate measure of the relative power levels of the fundamental tone's harmonics.

Just as we arrived at a coherent integration SNR gain expression in Eq. (11-14), we can express an incoherent integration gain, SNRincoh gain, in terms of SNR measured in dB as

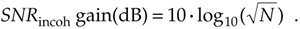
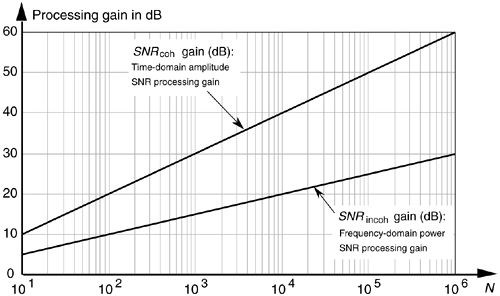
Equation (11-17) applies when the quantity being averaged represents the power of a signal. That's why we used the factor of 10 in Eq. (11-17) as opposed to the factor of 20 used in Eq. (11-14).[] We can relate the processing gain effects of Eqs. (11-14) and (11-17) by plotting those expressions in Figure 11-5.

[] Section E.1 of Appendix E explains why the multiplying factor is 10 for signal-power measurements and 20 when dealing with signal-amplitude values.

Figure 11-5. Time-domain amplitude SNR processing gain from Eq. (11-14), and the frequency-domain power SNR processing gain from Eq. (11-17), as functions of N.