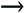DESIGNING A DISCRETE HILBERT TRANSFORMER | Chapter Nine. The Discrete Hilbert Transform

Discrete Hilbert transformations can be implemented in either the time or frequency domains. Let's look at time-domain Hilbert transformers first.

9.4.1 Time-Domain Hilbert Transformation: FIR Filter Implementation

Looking back at Figure 9-4, and having h(n) available, we want to know how to generate the discrete xi(n). Recalling the frequency-domain product in Eq. (9-1), we can say xi(n) is the convolution of xr(n) and h(k). Mathematically, this is:

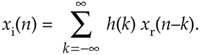
So this means we can implement a Hilbert transformer as a discrete nonrecursive finite impulse response (FIR) filter structure as shown in Figure 9-10.

Figure 9-10. FIR implementation of a K-tap Hilbert transformer.

Designing a traditional time-domain FIR Hilbert transformer amounts to determining those h(k) values so the functional block diagram in Figure 9-4 can be implemented. Our first thought is merely to take the h(n) coefficient values from Eq. (9-11), or Figure 9-9, and use them for the h(k)'s in Figure 9-10. That's almost the right answer. Unfortunately, the Figure 9-9 h(n) sequence is infinite in length, so we have to truncate the sequence. Figuring out what the truncated h(n) should be is where the true design activity takes place.

To start with, we have to decide if our truncated h(n) sequence will have an odd or even length. We make this decision by recalling that FIR implementations having anti-symmetric coefficients and an odd, or even, number of taps are called a Type III, or a Type IV, system respectively[1-3]. These two anti-symmetric filter types have the following unavoidable restrictions with respect to their frequency magnitude responses |H(w)|:

h(n) length:	Odd (Type III)	Even (Type IV)
	\|H(0)\| = 0	\|H(0)\| = 0
	\|H(ws/2)\| = 0	\|H(ws/2)\| no restriction

What this little table tells us is odd-tap Hilbert transformers always have a zero magnitude response at both zero Hz and at half the sample rate. Even-tap Hilbert transformers always have a zero magnitude response at zero Hz. Let's look at some examples.

Figure 9-11 shows the frequency response of a 15-tap (Type III, odd-tap) FIR Hilbert transformer whose coefficients are designated as h1(k). These plots have much to teach us.

Figure 9-11. H1(w) frequency response of h1(k), a 15-tap Hilbert transformer.

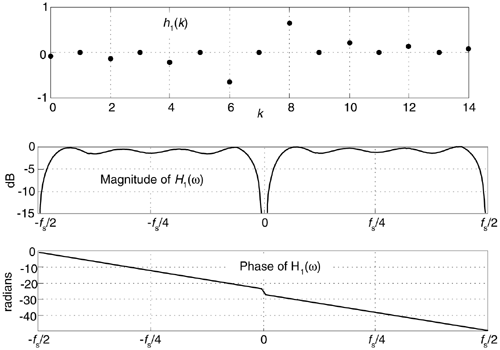
For example, an odd-tap FIR implementation does indeed have a zero magnitude response at 0 Hz and ±fs/2 Hz. This means odd-tap (Type III) FIR implementations turn out to be bandpass in performance.
There's ripple in the H1(w) passband. We should have expected this because we were unable to use an infinite number of h1(k) coefficients. Here, just as it does when we're designing standard lowpass FIR filters, truncating the length of the time-domain coefficients causes ripples in the frequency domain. (When we abruptly truncate a function in one domain, Mother Nature pays us back by invoking the Gibbs phenomenon, resulting in ripples in the other domain.) You guessed it. We can reduce the ripple in |H1(w)| by windowing the truncated h1(k) sequence. However, windowing the coefficients will narrow the bandwidth of H1(w) somewhat, so using more coefficients may be necessary after windowing is applied. You'll find windowing the truncated h1(k) sequence to be to your advantage.
It's exceedingly difficult to compute the HT of low-frequency signals. We can widen (somewhat) and reduce the transition region width of H1(w)'s magnitude response, but that requires many filter taps.
The phase response of H1(w) is linear, as it should be when the coefficients' absolute values are symmetrical. The slope of the phase curve (that is constant in our case) is proportional to the time delay a signal sequence experiences traversing the FIR filter. More on this in a moment. That discontinuity in the phase response at 0 Hz corresponds to p radians, as Figure 9-2 tells us it should. Whew, good thing. That's what we were after in the first place!

In our relentless pursuit of correct results, we're forced to compensate for the linear phase shift of H1(w)—that constant time value equal to the group delay of the filter—when we generate our analytic xc(n). We do this by delaying, in time, the original xr(n) by an amount equal to the group delay of the h1(k) FIR Hilbert transformer. Recall that the group delay G of a K-tap FIR filter, measured in samples, is G = (K–1)/2 samples. So our block diagram for generating a complex xc(n) signal, using an FIR structure, is given in Figure 9-12(a). There we delay xr(n) by G = (7–1)/2 = 3 samples, generating the delayed sequence x'r(n). This delayed sequence now aligns properly in time with xi(n).

Figure 9-12. Generating an xc(n) sequence when h(k) is a 7-tap FIR Hilbert filter: (a) processing steps; (b) filter structure.

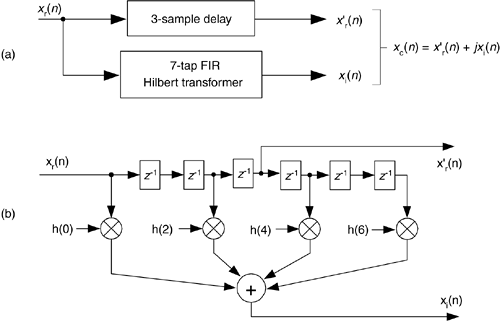
If you're building your odd-tap FIR Hilbert transform in hardware, an easy way to obtain x'r(n) is to tap off the original xr(n) sequence at the center tap of the FIR Hilbert transformer structure as in Figure 9-12(b). If you're modeling Figure 9-12(a) in software, the x'r(n) sequence can be had by inserting G = 3 zeros at the beginning of the original xr(n) sequence.

We can, for example, implement an FIR Hilbert transformer using a Type IV FIR structure, with its even number of taps. Figure 9-13 shows this notion where the coefficients are, say, h2(k). See how the frequency magnitude response is non-zero at ±fs/2 Hz. Thus this even-tap filter approximates an ideal Hilbert transformer somewhat better than an odd-tap implementation.

Figure 9-13. H2(w) frequency response of h2(k), a 14-tap Hilbert transformer.

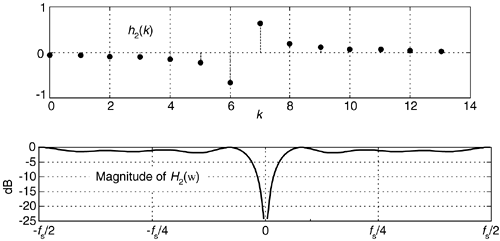
One of the problems with this traditional Hilbert transformer is that the passband gain in |H2(w)| is not unity for all frequencies, as is the x'r(n) path in Figure 9-12. So to minimize errors, we must use many h2(k) coefficients (or window the coefficients) to make |H2(w)|'s passband as flat as possible.

Although not shown here, the negative slope of the phase response of H2(w) corresponds to a filter group delay of G = (14–1)/2 = 6.5 samples. This requires us to delay the original xr(n) sequence by a non-integer (fractional) number of samples in order to achieve time alignment with xi(n). Fractional time delay filters is beyond the scope of this material, but Reference [4] is a source of further information on the topic.

Let's recall that alternate coefficients of a Type III (odd-tap) FIR are zeros. Thus the odd-tap Hilbert transformer is more attractive than an even-tap version from a computational workload standpoint. Almost half of the multiplications in Figure 9-10 can be eliminated for a Type III FIR Hilbert transformer. Designers might even be able to further reduce the number of multiplications by a factor of two by using the folded FIR structure (discussed in Section 13.7) that's possible with symmetric coefficients (keeping in mind that half the coefficients are negative).

A brief warning: here's a mistake sometimes even the professionals make. When we design standard linear-phase FIR filters, we calculate the coefficients and then use them in our hardware or software designs. Sometimes we forget to flip the coefficients before we use them in an FIR filter. This forgetfulness usually doesn't hurt us because typical FIR coefficients are symmetrical. Not so with FIR Hilbert filters, so please don't forget to reverse the order of your coefficients before you use them for convolutional filtering. Failing to flip the coefficients will distort the desired HT phase response.

As an aside, Hilbert transformers can be built with IIR filter structures, and in some cases they're more computationally efficient than FIR Hilbert transformers at the expense of a slight degradation in the 90o phase difference between xr(n) and xi(n)[5,6].

9.4.2 Frequency-Domain Hilbert Transformation

Here's a frequency-domain Hilbert processing scheme deserving mention because the HT of xr(n) and the analytic xc(n) sequence can be generated simultaneously. We merely take an N-point DFT of a real even-length-N xr(n) signal sequence, obtaining the discrete Xr(m) spectrum given in Figure 9-14(a). Next, create a new spectrum Xc(m) = 2Xr(m). Set the negative-frequency Xc(m) samples, that's (N/2)+1 m N–1, to zero leaving us with a new one-sided Xc(m) spectrum as in Figure 9-14(b). Next divide the Xc(0) (the DC term) and the Xc(N/2) spectral samples by two. Finally, we perform an N-point inverse DFT of the new Xc(m), the result being the desired analytic xc(n) time-domain sequence. The real part of xc(n) is the original xr(n), and the imaginary part of xc(n) is the HT of xr(n). Done!

Figure 9-14. Spectrum of original xr(n) sequence, and the one-sided spectrum of analytic xc(n) sequence.

There are several issues to keep in mind concerning this straightforward frequency-domain analytic signal generation scheme:

If possible, restrict the xr(n) input sequence length to an integer power of two so the radix-2 FFT algorithm can be used to efficiently compute the DFT.
Make sure the Xc(m) sequence has the same length as the original Xr(m) sequence. Remember, you zero out the negative-frequency Xc(m) samples; you don't discard them.
The factor of 2 in the above Xc(m) = 2Xr(m) assignment compensates for the amplitude loss by a factor of 2 in losing the negative-frequency spectral energy.
If your HT application is block-oriented in the sense that you only have to generate the analytic sequence from a fixed-length real time sequence, this technique is sure worth thinking about because there's no time delay heartache associated with time-domain FIR implementations to worry about. With the advent of fast hardware DSP chips and pipelined FFT techniques, the above analytic signal generation scheme may be viable for a number of applications. One scenario to consider is using the efficient 2N-point real FFT technique, described in Section 13.5.2, to compute the forward DFT of the real-valued xr(n). Of course, the thoughtful engineer would conduct a literature search to see what algorithms are available for efficiently performing inverse FFTs when many of the frequency-domain samples are zeros.

Should you desire a decimated-by-two analytic x'c(n) sequence based on xr(n), it's easy to do, thanks to Reference [7]. First, compute the N-point Xr(m). Next, create a new spectral sequence X'c(k) = 2Xr(k) for 1 k (N/2)-1. Set X'c(0) equal to Xr(0) + Xr(N/2). Finally, compute the (N/2)-point inverse DFT of X'c(m) yielding the decimated-by-two analytic x'c(n). The x'c(n) sequence has a sample rate of f's = fs/2, and the spectrum shown in Figure 9-14(c).

In Section 13.28.2 we discuss a scheme to generate interpolated analytic signals from xr(n).

URL http://proquest.safaribooksonline.com/0131089897/ch09lev1sec4