Section A.3. ARITHMETIC OPERATIONS OF COMPLEX NUMBERS
A 3 ARITHMETIC OPERATIONS OF COMPLEX NUMBERS
A.3.1 Addition and Subtraction of Complex Numbers
Which of the above forms for C in Eq. (A-1) is the best to use? It depends on the arithmetic operation we want to perform. For example, if we're adding two complex numbers, the rectangular form in Eq. (A-1) is the easiest to use. The addition of two complex numbers, C1 = R1 + jI1 and C2 = R2 + jI2, is merely the sum of the real parts plus j times the sum of the imaginary parts as
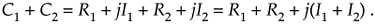
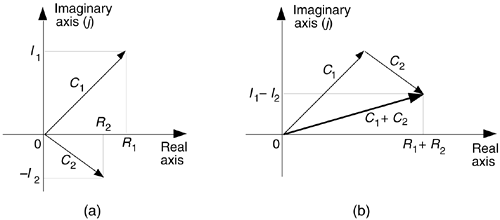
Figure A-3 is a graphical depiction of the sum of two complex numbers using the concept of phasors. Here the sum phasor C1 + C2 in Figure A-3(a) is the new phasor from the beginning of phasor C1 to the end of phasor C2 in Figure A-3(b). Remember, the Rs and the Is can be either positive or negative numbers. Subtracting one complex number from the other is straightforward as long as we find the differences between the two real parts and the two imaginary parts separately. Thus
Equation A-11
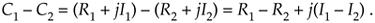
Figure A-3. Geometrical representation of the sum of two complex numbers.
An example of complex number addition is discussed in Section 11.3, where we covered the topic of averaging fast Fourier transform outputs.
A.3.2 Multiplication of Complex Numbers
We can use the rectangular form to multiply two complex numbers as
Equation A-12
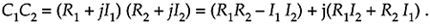
However, if we represent the two complex numbers in exponential form, their product takes the simpler form
Equation A-13
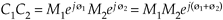
because multiplication results in the addition of the exponents.
As a special case of multiplication of two complex numbers, scaling is multiplying a complex number by another complex number whose imaginary part is zero. We can use the rectangular or exponential forms with equal ease as follows:
Equation A-14

or in exponential form,
Equation A-15
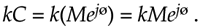
A.3.3 Conjugation of a Complex Number
The complex conjugate of a complex number is obtained merely by changing the sign of the number's imaginary part. So, if we denote C* as the complex conjugate of the number C = R + jI = Mejø, then C* is expressed as
Equation A-16
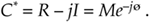
There are two characteristics of conjugates that occasionally come in handy. First, the conjugate of a product is equal to the product of the conjugates. That is, if C = C1C2, then from Eq. (A-13),
Equation A-17
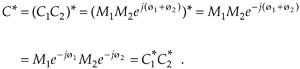
Second, the product of a complex number and its conjugate is the complex number's magnitude squared. It's easy to show this in exponential form as
Equation A-18
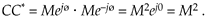
(This property is often used in digital signal processing to determine the relative power of a complex sinusoidal phasor represented by Mejwt.)
A.3.4 Division of Complex Numbers
The division of two complex numbers is also convenient using the exponential and magnitude and angle forms, such as
Equation A-19

and
Equation A-19'
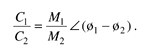
Although not nearly so handy, we can perform complex division in rectangular notation by multiplying the numerator and the denominator by the complex conjugate of the denominator as
Equation A-20

A.3.5 Inverse of a Complex Number
A special form of division is the inverse, or reciprocal, of a complex number. If C = Mejø, its inverse is given by
Equation A-21
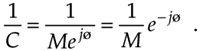
In rectangular form, the inverse of C = R + jI is given by
Equation A-22

We get Eq. (A-22) by substituting R1 = 1, I1 = 0, R2 = R, and I2 = I in Eq. (A-20).
A.3.6 Complex Numbers Raised to a Power
Raising a complex number to some power is easily done in the exponential form. If C = Mejø , then
Equation A-23
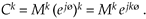
For example, if C = 3ej125°, then C cubed is
Equation A-24
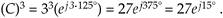
We conclude this appendix with four complex arithmetic operations that are not very common in digital signal processing—but you may need them sometime.
A.3.7 Roots of a Complex Number
The kth root of a complex number C is the number that, multiplied by itself k times, results in C. The exponential form of C is the best way to explore this process. When a complex number is represented by C = Mejø, remember that it can also be represented by
Equation A-25
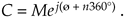
In this case, the variable ø in Eq. (A-25) is in degrees. There are k distinct roots when we're finding the kth root of C. By distinct, we mean roots whose exponents are less than 360°. We find those roots by using the following:
Equation A-26
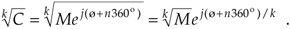
Next, we assign the values 0, 1, 2, 3, . . ., k–1 to n in Eq. (A-26) to get the k roots of C. OK, we need an example here! Let's say we're looking for the cube (third) root of C = 125ej(75°). We proceed as follows:
Equation A-27
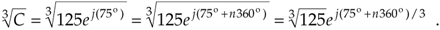
Next we assign the values n = 0, n = 1, and n = 2 to Eq. (A-27) to get the three roots of C. So the three distinct roots are
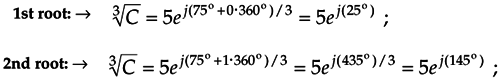
and
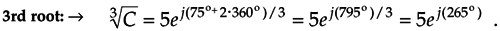
A.3.8 Natural Logarithms of a Complex Number
Taking the natural logarithm of a complex number C = Mejø is straightforward using exponential notation; that is
Equation A-28
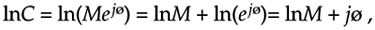
where 0  ø < 2p . By way of example, if C = 12ejp/4, the natural logarithm of C is
ø < 2p . By way of example, if C = 12ejp/4, the natural logarithm of C is
Equation A-29
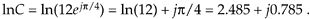
This means that e(2.485 + j0.785) = e2.485 · ej0.785 = 12ejp/4.
A.3.9 Logarithm to the Base 10 of a Complex Number
We can calculate the base 10 logarithm of the complex number C = Mejø using
Equation A-30
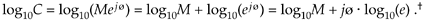
Of course e is the irrational number, approximately equal to 2.71828, whose log to the base 10 is approximately 0.43429. Keeping this in mind, we can simplify Eq. (A-30) as
Equation A-31
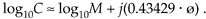
Repeating the above example with C = 12ejp/4 and using the Eq. (A-31) approximation, the base 10 logarithm of C is
 For the second term of the result in Eq. (A-30) we used loga(xn) = n·logax according to the law of logarithms.
For the second term of the result in Eq. (A-30) we used loga(xn) = n·logax according to the law of logarithms.
Equation A-32
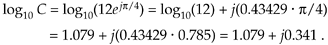
The result from Eq. (A-32) means that
Equation A-33

A.3.10 Log to the Base 10 of a Complex Number Using Natural Logarithms
Unfortunately, some software mathematics packages have no base 10 logarithmic function and can calculate only natural logarithms. In this situation, we just use
Equation A-34
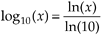
to calculate the base 10 logarithm of x. Using this change of base formula, we can find the base 10 logarithm of a complex number C = Mejø; that is,
Equation A-35
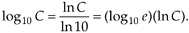
Because log10(e) is approximately equal to 0.43429, we use Eq. (A-35) to state that
Equation A-36
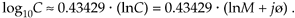
Repeating, again, the example above of C = 12ejp/4, the Eq. (A-36) approximation allows us to take the base 10 logarithm of C using natural logs as
Equation A-37

giving us the same result as Eq. (A-32).
URL http://proquest.safaribooksonline.com/0131089897/app01lev1sec3
 |
Amazon |  |
